It's a small world, after all

[From the archives; originally posted November 28, 2005]

Have you ever wondered how Kevin Bacon and the lights of fireflies related to malaria and power grids? I know it's something that's kept me up many a sleepless night. One word: interconnections.

Many of you have probably heard of the "Six degrees of Kevin Bacon"game. This is based on the work of Stanley Milgram beginning in the 1960s, and brought up again more recently in a 1998 Nature paper, "Collective Dynamics of 'Small-World' Networks," by mathematicians Watts and Strogatz. Milgram conducted a number of studies using his "lost letter technique," in which letters were sent out and then needed to be forwarded onto reach their destination. In one instance, Milgram sent out 160 letters to individuals in the midwest, with instructions to pass them along to acquaintances who would be most likely to reach his stockbroker friend back east. Almost all of the letters that reached the stockbroker did so via one of 3 friends, and most did it within 6 steps--hence the "six degrees of separation" idea. Similarly, Duncan Watts first became interested in the "small world problem"--the idea that all of us are more closely connected than we realize--after watching fireflies flash in synchrony, and wondering how they accomplished that. What Watts, Strogatz, Milgram, and others were investigating boiled down to a series of links in a network--hubs and connectors. As Watts and Strogatz showed in their 1998 paper, all it took to make a "small world" from a regular network was the addition of a few "short cuts" (see figure from their paper, above). This elegant and seemingly simple structure of networks explains not only connections between movie stars and scientists but also cellular metabolism, ecology webs and the World Wide Web itself.

Another "small world" phenomenon is disease transmission. Social architecture affects, and explains, factors that impact the spread of disease--the people we are in contact with, and in the cases of sexually transmitted diseases, the people we sleep with. At the base of this phenomenon in infectious diseases is an idea called the "tipping point." This is something epidemiologists have discussed much in recent months regarding the potential of an avian influenza pandemic--tiny influences can have startling effects. A simple mutation may make a virus more easily transmitted between humans. Given the right environment, this may allow the virus to sweep through a population, causing a world-wide outbreak. Under different conditions, it may cause a few infections and fade away; a few factors may make all the difference. Mathematical modelers can examine these factors in computer simulations in order to determine if a disease will burn out, remain endemic in a population, or become an epidemic. A critical determining factor affecting these outcomes is the basic reproductive rate of a disease (R0). If R0 is less than 1 (each case infects less than one additional individual), a self-sustaining epidemic is not possible. If it is equal to 1, the disease will become endemic in a population. If R0 exceeds one, the disease may become epidemic; the larger the number, the more likely this outcome is. But, while this number is useful, one must keep in mind that R is an average over the population--it may be much higher or lower in subsets of the group.

Early work in this area did not take this difference into account, and assumed that individuals in a population had an equal chance of transmitting the disease. However, reality does not bear this out, leading to the proposal of the "20/80 rule," which suggests that approximately 20% of the most infectious individuals are responsible for 80% of the disease transmission. This was most recently demonstrated by an analysis of the 2003 SARS outbreak (see figure, from MMWR 52(18);405-411), but has also been seen with AIDS and other STDs. With AIDS, we recognize that "core groups" of infected individuals are often responsible for large outbreaks of disease. What we see when we examine this graphically is a "small world" network: a series of hubs and connectors, with the largest hubs---termed "superspreaders" (the numbered dots in the picture above)--responsible for a disproportionately large number of secondary cases. This may be due to the fact that the superspreaders simply have a higher number of contacts; they may have a co-infection that leads to increased pathogen shedding, meaning the contacts they have are more efficiently exposed; they may have an undiagnosed illness, leading to an extended period of transmission; or they may have a combination of the above. For example, imagine a sex worker with both HIV and a secondary STD, such as gonorrhea. By virtue of her occupation, she will be in contact with a large number of individuals. HIV may lead to an increase in bacterial load, exposing her clients to a larger dose of N. gonorrhea than the "average" infected person; and her lack of health care means she has been treated for neither STD--potentially spreading both for years, until she is too sick to continue working. In this case, there are multiple explanations for why she would be a superspreader.

It takes careful epidemiological analysis to identify these superspreaders, however. One limitation of epidemiological analysis is that populations are generally divided into homogeneous subgroups--people of the same age, or race, or occupation, etc. This makes it possible to carry out studies comparing groups of individuals, but at the same time, it creates false divisions; life is always messier. A new paper published in Nature seeks to investigate some of this "mess," addressing the heterogeneity of transmission number among individuals and its effect on spread of disease. This new study by Lloyd-Smith et al., instead of using R0, investigates ν, the individual reproductive number. To examine this, they looked at previously published accounts of disease transmission where contacts had been traced, and determined ν for a number of different diseases and patients (see figure, below).

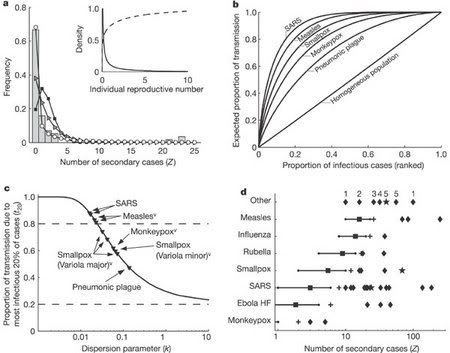
To sum up their findings, they suggest that disease with a high variation in ν show infrequent, but explosive, epidemics after introduction of a single case, a statement again borne out by an examination of the epidemiology of SARS, a disease which showed a high variation in ν. Indeed, many cities were exposed to SARS, but very few had explosive outbreaks. Is this universal? It will take more careful studies to determine that, but it suggests a new avenue of investigation.

Indeed, knowledge of the architecture of these outbreaks has immediate real-world applications. If the superspreaders could be identified early in an outbreak, interventions (vaccination, isolation/quarantine, treatment) could be targeted to this group. For example, another recent report highlights this same conclusion for malaria: identifying and targeting the superspreaders could reduce the disease burden enormously. Additionally, this work suggests, again, that we need better surveillance in order to detect these events while they are in progress. We can't control superspreaders that we aren't aware of, or only identify retrospectively, weeks, months, or years down the line.

Finally, this work--and indeed, much of the work done in the field of network theory--also points out, again, how things that appear to be "designed" can be the product of chance and circumstance. Each of these "small worlds" reveals a very similar architectural design. Each is dominated by hubs--a few extremely well-connected individuals, or web sites, etc. Additionally, this is not merely a qualitative difference: instead, they have a specific mathematical signature, which is nearly identical from one network to the next. I won't go into the details, but Mark Buchanan has written a very layman-friendly book on the subject. (To be complete, Watts and Strogatz have also written books on the subject, but I've not read them yet). In Nexus, Buchanan notes:

What we see then is a kind of natural order that for mysterious reasons seems to well up in networks of all kinds and that does so despite the complexities of their individual histories....In biology, Charles Darwin's idea of evolution by natural selection offers an extremely powerful organizing framework within which historical accidents take place. In the context of networks, there must also be some deeper principle at work.

Along a similar line of thought, Nobelist Herbert Simon once said, "The purpose of science is to find meaningful simplicity in the midst of disorderly complexity." Network theory has shown how this can be done, and unlike "intelligent design," has immediate practical applications in a vast range of fields.

[Since this is a topic that I find fascinating but is a bit outside of my area of expertise, I'll also link to this criticism of "scale-free" networks by Evelyn Fox Keller].