We're holding a rock, and we drop it. What happens?
There's lots of methods for treating this problem. We've done it with Newton's laws of force, and we've done that in more than one way. We've done the Lagrangian formulation in terms of minimizing the classical action. I don't think we've done the quantum mechanical propagator yet, but we'll get to it. Today we'll do the Hamiltonian formulation.
Like the Lagrangian, it's a formulation of mechanics that's based on the relationships between energy, momentum, and position. Define a quantity H called the Hamiltonian, and set it equal to the sum of the kinetic and potential energy of the particle in question. We'll call the position of the rock with the label y and denote its derivative (the velocity) with a y-dot. This gives us an equation for H:
This is a good start. Now we'll get to the heart of the matter and write down Hamilton's equations, which describe the time development of the system:
Here q represents whatever coordinate we happen to be using. Here we only have one of them, the vertical position y. By the same token, p represents the momentum in this direction. In general the relationship between these generalized momenta and velocities will be more complicated than our situation here and we'd have to do some manipulation to the Lagrangian in order to fund out just what the appropriate equations are. But here things are simple, the generalized momentum is just the ordinary momentum, mass times velocity . That means we won't even need the second of Hamilton's equations either. The first will do the trick. Behold! Well ok, it's not that dramatic.
But we know what p is, and so we know what the derivative of p is:
A falling rock accelerates downward with acceleration -g. Did we already know this, and are there easier ways to find it out? Sure, in this case. But not in every case. And for theoretical work the Hamiltonian formation is often preferable. It's always good to have another tool in the toolkit.
- Log in to post comments
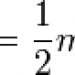


The first Hamiltonian problem I was ever asked to solve was a heavy hollow ring rolling down an inclined plane that was free to slide around on a frictionless surface. An ugly formulation, but still very satisfying.
Is it obvious that
D/Dy((dy/dt)^2) = 0 (D=partial diff)?
I mean obvious in the context of the post, not to mathos who wouldn't need to read this post in the first place.
This is all totally wrong. There is no gravitational term in the Standard Model Lagrangian for gravitational potential. Therefore gravity doesn't exist and the rock doesn't fall.
(advance apologies for my appalling pedantry)
"A falling rock accelerates downward with acceleration -g"
that is a double negative. you mean upwards with -g, which is downwards.