Built on Facts

Let’s say you have a table. This table is better than your average table. It’s perfectly level, absolutely flat to within the thickness of an atom over its entire surface. In fact, this table isn’t even made of atoms. You called up Plato and ordered the platonic ideal of a flat table.

Now you set this table down in your dining room and have Plato’s deliverymen install the table so that it’s perfectly flat with respect to the earth’s surface. Then you take a ping-pong ball and set it down toward the edge of the table. What happens?

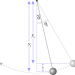
It doesn’t stay still. It will roll to the center of the table. The reason is that the table being level doesn’t mean that gravity is pointing locally downward everywhere on the table. A picture is worth a thousand words here, and for clarity let’s make this table very big. Very big.

Here x is how far from the center of the table the ball happens to be at that moment. R_e is the radius of the earth. You can see how gravity will be pulling the ball toward the center of the earth, and that means there’s a component of force parallel to the table. We can set this up as a differential equation, with force on the right and mass times acceleration on the left:

Now we see that the mass appears on both sides, so it cancels. We also know that the sine of theta is for small angles approximately equal to the tangent of theta. And tangent of theta is the side opposite over the side adjacent. This puts our differential equation in this form:

Now it’s immediately clear if you’ve been in the physics business a while that this is the differential equation describing simple harmonic motion. It’s the same kind of thing as a pendulum swinging back and forth or a spring oscillating up and down. What’s especially important about simple harmonic motion is that it takes the same amount of time to execute one cycle of motion no matter how large the initial amplitude is. A barely nudged pendulum swinging at one stroke per second will also swing at one stroke per second if the push is larger. It has a longer distance to travel but it’s also moving faster. The two effects cancel out. The angular frequency of an object in simple harmonic motion is the square root of the term in front of the x. But let’s convert that to the period T, which is the time required to make one complete oscillation:

So the ball will roll back and forth on your table once every 84 minutes. You’d only be able to see this motion on a tremendously huge and perfectly flat table, otherwise imperfections in the flatness, local gravity effects, friction, and what have you will ruin the very small forces involved. We’re talking micronewtons at best for actual tabletop displacements.

Connoisseurs of physics problems will probably recognize that 84 minutes number as the period of an object falling through the earth. If you were to drill a tunnel straight down to the other side of the world, neglecting air resistance you’ll fall back and forth in 84 minutes. This means if you decided to step out at the far end of the tunnel your journey would take 42 minutes.

Actually it’s more interesting than that. Turns out that you don’t even have to dig the tunnel straight down. If I gun a tunnel from here to Paris, it would still take 42 minutes. This is not obvious and the math is somewhat trickier than this, but perfectly tractable nonetheless. We’ll do it here eventually. This particular tabletop thought experiment is something of a limiting case of the tunnel problem.

I don’t know if there are any flat surfaces long enough to actually try an experiment like this in real life. The SLAC beam tunnel, perhaps? Now there’s a side project for any clever researchers with some spare time while the computers are crunching data…

Comments

#1 Robert
November 11, 2008

Isn’t the denominator of sine theta actually sqrt(x^2 + Re^2), the hypotenuse?
#2 Joshua Zelinsky
November 11, 2008

I doubt the SLAC is good enough to do this well. While the tunnel itself is very flat, I’m not sure that the local imperfections of the tunnel are small enough. But it would be cool for someone to try and check.
#3 Matt Springer
November 11, 2008

Quite right, Robert. Somehow when I wrote this late last night I somehow garbled my explanation of the small-angle approximation into saying tan(x) = sin(x), which is of course true only the small x limit. Give me a sec and I’ll fix it.
#4 Tim Gaede
November 11, 2008

Actually, because Earth is not uniformly dense, the period is shorter than 84 minutes.

Since the density of the earth goes up nearer the center, the pull of gravity is not proportional to distance. In fact, it actually goes up and down a bit before plunging as we move through the core.

Using geological data, I created a model of the earth that was composed of five layers whose density was a linear function of distance from the center. This made integration easy, though tedious. The mass of my model was the same as the accepted value for Earth. I determined that the period would actually be 76 minutes 45 seconds.
#5 CCPhysicist
November 11, 2008

That is a really nice variant of the usual “tunnel through the earth” problem (a problem that is much older than you are!), since it looks more plausible and is accessible to demonstration in our lecture room.

Checking your numbers:
If you have a 2m “frictionless” track that has been perfectly leveled, the max displacement of 1 m results in a restoring force of (1 m)/Re times the weight. Use a 650 g cart (weight about 6.37 N) and you have a restoring force of exactly 1 uN. Sweet.

Experimental complications:
Calculate the gravitational force due to the lecturer, the Moon, or Jupiter, or a room full of students. No wonder gravitational experiments are so hard.

It is an interesting question whether the SLAC tunnel’s concrete floor was “leveled” by gravity when it was poured or against forms set with optical surveying instruments. Using your geometry, that is, x = 1.6 km, the level table would be about 20 cm above a “level” surface at either end of the tunnel.
#6 CCPhysicist
November 11, 2008

Should have thought of this when I posted: The simple test for the SLAC tunnel is to plug up the drains and put 6″ of water in it … at the center. Will the water reach the ends of the tunnel, or be deeper in the center?
#7 Matthias
November 11, 2008

Thank You!

I could never get my head around the 84 minutes when thinking about the tunnel as being drilled from one point into different directions. Rather thinking of it as the table being at different distances from the earth’s center helped a lot.
#8 jayh
November 11, 2008

Even these details are of interest to somebody.

years ago I remember watching a game show (Jeopardy?) when the first interviewed the contestants. One fellow’s job was actually micro mapping gravity, but that’s all he could say about it because his job is basically classified; used by the military for plotting missile trajectories.

Then there is this really cool family physics trip:

http://www.leapsecond.com/great2005/tour/

He’s just lucky that national security type didn’t interpret his van full of electronics and batteries as a ‘terrorist threat’.
#9 derek
November 11, 2008

Actually, as a connoisseur of space physics problems, I only recognised 84 minutes as the period of an Earth orbit at sea level. At realistic heights, a couple of hundred miles up, where the Shuttle and International Space Station are, it’s a bit closer to 90 minutes.
#10 Paul Johnson
November 11, 2008

Impressive but can you account for the earth’s rotation if this were placed at the tropics? If the ball were rolling north south at the tropics would it not start to roll around in weird shapes? better yet, depending on the width of the table and the speed of the ball should it not fall off entirely?

What about at the north pole? shouldn’t it start making petal like rotations? I’m never getting over the coriolis effect
#11 Uncle Al
November 11, 2008

The earth curves about 8 inches/mile – but this is not the horizon problem. In round numbers, where “x” is distance in miles and “c” is curvature in feet.

c = (2/3)x^2

The first thermonuclear device, Mike, had a Krause-Ogle box 1.7 miles long. SLAC is 2 miles long, LIGO’s arms are 2.5 miles long. Laser-leveling is a mixed blessing. Light falls at gee = 19.6 m/sec^2 but it gets from here to there at a foot/nanoseond.

Free fall chord tunnels, 40 minutes to anywhere with only friction compensation needed, have three issues: A rather large volume of rock must be excavated. The air must be pumped out to vacuum (the first few runs are displacement vacuum pumps themselves). 80-100 miles deep is the diamond stability zone.
#12 ossicle
November 11, 2008

Hm, I was confused by the transition from the penultimate equation (for acceleration) to the final equation (for period) until I went to wikipedia and read that for small angle approximation, T = 2pi(length of “string”/g).

Given that, though, what’s the point of Matt’s second to last sentence in the paragraph before the equation for T, “The angular frequency of an object in simple harmonic motion is the square root of the term in front of the x.” I’m sure that’s correct, but I’m not getting why it’s worth mentioning. My presumption would be that it allows us to derive the equation for T (i.e., T = 2pi(length of “string”/g)) but I don’t see how. Probably because I’m an ignoramus. Any help is welcome, though.

-Oss

Er, sorry, but in the final equation — for the period T — I get that T = 1/f and that’s why sqrt(g/Re) –> sqrt(Re/g) is where I get lost. How is Matt going from the preceding equation — acceleration equals (-g/Re)*x — to the equation for T?
#13 ossicle
November 11, 2008

Gah! Sorry, the words after my sig in the above post are superfluous, I should have deleted them — they were part of my initial, aborted way of phrasing my post.
#14 Andrew
November 11, 2008

By the way, 84 minutes is also the natural period of oscillation for an Earth-surface inertial navigation system such as is used in aircraft, surface ships and submarines http://en.wikipedia.org/wiki/Schuler_period
#15 Matt Springer
November 11, 2008

Ossicle, angular frequency is two pi times the frequency f. The reason for using angular frequency is just to make the sin and cos terms in the actual solution of the differential equation easier to work with. Since we’re only after the period here, we don’t really need to worry about any of it except for finding T. Formally speaking,

w = 2 pi f, and T = 1/f

which lead to

T = 2 pi (1/w)

Edit: Blarg, apparently special characters don’t typeset properly in the comments. I’ve renamed the angular frequency to w above to work around that.
#16 Eric Lund
November 12, 2008

Matt, I know you have to use the HTML escape sequences to get accented Latin characters. Are there comparable escape sequences for Greek letters? In other words, does typing “ω” give you an ω? (Consider this an experiment: if that last sentence typeset correctly, the answer is yes.)
#17 d
November 12, 2008

Perhaps you could use dry ice to create a gas-bearing; a sort of “frictionless hockey puck” to replace the ball. That would lower the bar some relative to table flatness.

As was pointed out, coriolis is a factor. Intuition (and 8th grade physics) tells me that it would not allow a real setup to last long anyway (ie, the “ball” would fall off the table), except perhaps in an east-west scenario. Even there, wouldn’t coriolis cause the ball to overshoot to the west, and undershoot to the east?
#18 d
November 12, 2008

Ok, my eight grade physics teacher (may he rest in peace, from now on, anyways) just called and he says the ball won’t fall off the table because “the center of the table is the ‘lowest’ point in the system…”
#19 ossicle
November 12, 2008

Thank you, Matt!