Here's sin(x).

What, you don't believe me? Ok, ok, I'm leaving something out. Let's do some background before I tell you what it is.
The first thing we need is the incredibly interesting and important Euler's formula. It's the key that relates the exponential and trigonometric functions. We won't pause to figure out why it's true, for now we'll just take it as a given:

Now replace x with -x, and we'll use the fact that cos(x) is the same as cos(-x), and sin(-x) is the same as -sin(x).

So that's two ways of saying the same thing. Now we'll subtract the second equation from the first. The cosines will cancel and we'll end up with

Now divide out that 2i, and we've figured out a new way to write the sine function:

What I've done in the above graph is let x = i t, where t is a usual real number in this case between -4 and 4. Plugging this into the above expression means what I'm actually graphing is

This is a pure imaginary number, and so I'm actually plotting the magnitude of that imaginary quantity.
Is all this useful for anything. You bet it is! This kind of manipulation between exponential and trig functions permeates mathematics and physics in almost every possible context. Contour integrals, differential equations, the theory of real and complex functions, you name it. Incidentally, you can find the same sort of relationship for the cosine and tangent functions using the same method. Between them it makes proving the various high-school trig identities much easier. Cool stuff, and very useful.
Homework for the mathematically inclined reader: tan(z) is undefined by virtue of a vertical asymptote at z = n*pi/2 for all odd n. Is it undefined for any z which is not a real number? If so, where?
- Log in to post comments

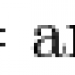
Since tan(z) = sin(z)/cos(z), your question is equivalent to whether cos(z) has any zeroes for z not purely real. By a similar argument to what you have outlined above
cos(z) = (eiz + e-iz)/2
By the addition formula, and defining z = x + iy where x and y are real numbers
cos(z) = cos(x) cos(iy) - sin(x) sin(iy)
which vanishes when
tan(x) = tan(iy) (when cos(x) != 0 and cos(iy) != 0)
or cot(x) = cot(iy) (when sin(x) != 0 and sin(iy) != 0).
Now, as you have shown above, sin(iy) = 0 iff y = 0, and the same is true of cos(iy). So for y != 0 we can always use one of these formulae, and it is straightforward to construct cases where the first is satisfied. Therefore there exist complex numbers with nonzero imaginary parts where tan(z) diverges.
(For those who haven't caught on yet: The function plotted goes by the name of hyperbolic sine, where sinh(z) = (ez - e-z)/2.)
Typo correction in above: Replace "iff" with "only if".
Your substitution from ix to t involves a sign error. I think.
eiz=-e-iz requires that the two sides have the same magnitude, i.e. that iz have the same real component as -iz, i.e. that the real component of iz be 0, i.e. that the imaginary part of z be 0. z must be real for cos(z) to be 0.
About those zeroes of cos(z), another way to see it is to use the Euler product decomposition:
sin(πz)/(πz) = ... (1+z/2)(1+z)(1-z)(1-z/2)(1-z/3)...
(translating by (π/2) gives an equivalent decomposition for the cosine function). The Euler product gives the zeroes of the function. (Well, this is a nontrivial theorem, since an infinite product of non-null factors may converge to zero; but the Euler products behave well).
OK, math is really really cool...
#3, quite right. I did it right in the graph and my notes but somehow I typed the LaTeX wrongly for the typeset equation. Fixed now!
So tell us how the big test went.
I am more than somewhat rusty on the math, but I have maintained a fondness for plots of functions ever since my early high school days when I was given a copy of a wonderful book "A Book Of Curves" by E. H. Lockwood (a pdf is available here: http://www.archive.org/details/bookofcurves006299mbp). It focus is on how to plot a large collection of different curves using drawing board tools commonly available in 1961. I think this group may enjoy it too.
Gaffer, sir, I would enjoy it much more if the link led to it, thank you so much. :)
#9,
Just erase the period and close parenthesis at the end of his link and it will get you there.
Cy
I thought the sneaky trick was that tan(x), like all trig functions, has an essential singularity at the point at infinity (which is, of course, not a real number, but is part of the Riemann sphere).