Just 24 light-hours away it's still Sunday, right? Oh well. On to the math!
If you ask a mathematician to define a circle, you'll probably hear something along the lines of "A circle is the set of points in a plane equidistant from a given center point. The name of the distance from the center is the radius." A mathematician will state it more precisely, but that's the gist. As a technical matter - and mathematicians love technical matters - this is actually somewhat different from what kids learn about circles in school. Kids would probably say a frisbee is a circle, but really it's more of a disc. A disc is the area contained within a circle, which is the same as saying a circle is the boundary of a disc.
Having made that note to satisfy the geometry-savvy readers, I'll promptly go back to the grade-school convention and say "circle" when formally I mean disc. Ditto for "sphere", which mathematically is properly the surface of a ball in 3-d space, but here I'll take spheres to have a volume and circles to have an area.
So after all that rigmarole, we want to think more generally. Spheres have volume and circles have area, concepts which are more or less specialized to three dimensions and two dimensions respectively. But there's nothing stopping us from thinking about them more generally, as a type measure of the space. The name for that measure varies depending on the number of dimensions, but in both cases it's perfectly possible to think of area and volume as just measuring the amount of space in a region. Thinking along those general lines we might as well scrap the word "area" entirely and just rename the 2-d concept of area to "2-volume", while what we previously called volume can be renamed "3-volume".
Heck, while we're at it why not just call circles "2-spheres" and spheres "3-spheres"?
For a 2-sphere (formerly called a circle) of radius r, the 2-volume (or what we used to call area) is:
For a 3-sphere (formerly just called a sphere) of radius r, the 3-volume (or what we used to just call volume) is:
We've seen those formulas before, in middle school or earlier. Aside from our wonky renaming nothing has changed. Try another case for yourself. What's the 1-volume of a 1-sphere? Think about it for a minute, and then go on to the next paragraph.
In one-dimensional space, we just have a line. Pick a point and call it the center of our 1-sphere. By direct copying of our definitions for spheres in 2 and 3 dimensions, you pick a radius, call it r, and mark all the points which are a distance r from the center. But we're on a line, and so there's only two such points - one on each side of the center. The distance from the center to one of those points is r. Thus the total 1-volume (you may have realized 1-volume is our general way of saying "length") of a 1-sphere is just the distance from one side of the 1-sphere to the other, passing through the center. That is:
Whew. That seems like an absurd amount of effort to go through to say a few basic geometrical facts that we already knew. Is all this renaming really worth anything?
No, it's all garbage.
Ok, ok. I'm just kidding. Turns out this stuff is in fact both very important and very useful. Not so much for the old 1, 2, and 3 dimensional cases we're used to, but for higher dimensions. Now as far as we know there aren't literal higher spatial dimensions, protests of string theorists notwithstanding. But there are times when we might have a huge set of coordinates whose values happen to be geometrically connected in a way corresponding to our definition of the n-sphere.
As an example, take a box full of gas molecules. Each of them are going to be described by three numbers representing the momentum in the x, y, and z directions. The total energy of those particles is going to be described as proportional to the sum of the squares of those momentum coordinates. So if you have 10 particles you'll have 30 momentum variables, each of which is squared and added together. That's in a sense like an abstract 30-sphere. For many calculations (most especially the entropy) we want to know how many combinations of those numbers correspond to a certain energy - and the energy is the radius of the 30-sphere. To do that, we need the 30-volume of a 30-sphere.
That paragraph probably lost a few people. I had to stare cross-eyed at the statistical mechanics book for a little while while I was working through it too. In short, we'll just say that there's numerous physical reasons you might need to know the "volumes" of some preposterously high dimensional "spheres". And sure enough, there's a function that can tell us what those volumes are. It's our Sunday Function. The n-volume of an n-sphere of radius r is:
Where that thing in the denominator of the fraction is itself the gamma function. That may be a more bizarre expression than you or I might have hoped but I'm sorry to say that it's true nonetheless.
I know of two ways to prove it*. You can do the straightforward method and construct a generalization of spherical coordinates in n dimensions and integrate over them. Here "straightforward" means that it's monstrously horrible and I have no doubt that I couldn't do it without a reference in front of me. There's also a trick you can do involving Gaussian integrals. It's still rather head-spinning but nonetheless more elegant. I might save that for another time.
I'm not sure I'd describe any of this as useful outside of some fairly deep and abstract physics. On the other hand that deep and abstract physics is intimately entangled with our most basic understanding of the the statistical behavior of... well, pretty much everything. It's a straight-line path from this stuff to engineering as mundane as the way your car engine works. I tip my hat to whoever first figured out what volume meant in higher dimensions. It was a pretty awesome feat.
*I'm doing neither of them in this post, though I'll probably do at least the second later on. If you just can't wait they're both in the appendices of Pathria's Statistical Mechanics.
- Log in to post comments
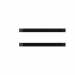

I doubt you'd actually need the reference to do the straightforward integration method. The proof is technically unpleasant but there are no steps that are inherently difficult or tricky. It just takes forever.
I can sketch the proof easily. As Joshua says, it's not too difficult to generalize spherical coordinates to N dimensions. Proof would be by induction: you have already shown that it holds for N <= 3; all you need to do is to show that assuming it to be true for some arbitrary N implies that it also holds for N + 1 (or N + 2, in a pinch). Of course, carrying out the proof would take some tedious effort, but it would still be straightforward.
(Reposting with correct HTML code)
I can sketch the proof easily. As Joshua says, it's not too difficult to generalize spherical coordinates to N dimensions. Proof would be by induction: you have already shown that it holds for N <= 3; all you need to do is to show that assuming it to be true for some arbitrary N implies that it also holds for N + 1 (or N + 2, in a pinch). Of course, carrying out the proof would take some tedious effort, but it would still be straightforward.
Are there any cases where n is not a positive integer? Otherwise, you can replace the gamma function with '(n - 1)!', correct?
Good points. I suppose I could do it without a reference. But I really wouldn't want to!
Helge: For our purposes n is always a positive integer, but that still leaves us with a non-integer as the argument for the gamma function for odd n. Either way I'm told that in pure math the expression is also meaningful for non-integer n. I've not yet come across a physical reason to need the concept generalized that far. But weirder things have happened, and for all I know volumes of irrational-dimensional hyperspheres may be important in some strange regions of theoretical physics.
To solve your apparent language difficulties it is, the area 'enclosed' by a circle and the volume 'enclosed' by a sphere.
Ummm. I just followed your link the the gamma function and found that for real integers (as opposed to complex numbers), Gamma(n) = (n - 1)! (where the ! here used in both senses). Since you were focusing on real integers, why mess with our heads like that?factorial.
Oh I see now: (n/2) + 1 is not an integer for odd n.
If you were doing pure geometry, you wouldn't want to define a circle at all. The definition uses the concept of sets, which is another area of mathematics. Instead, "circle" would be an undefined concept like "line", "point", "congruent", etc. Then you'd need some axioms about circles. I don't think many geometers take that approach, though.
Interesting post! Another funny fact about volume of N-dim. sphere with unit radius is that for N > 5 the volume actually starts to decrease with more dimensions. When I heard that in my calculus lecture, I found it quite intriguing (although the interest faded away somewhat after our prof. filled several blackboards while proving the formula).
Interesting post, indeed! I can't help but wonder if we'll ever get over the arbitrary convention of designating 3.1415... with its own special symbol. It seems that the square root of pi is a much more interesting constant, deserving its own symbolic representation (pick a Greek letter, I say gamma); it would certainly make the above formula appear more elegant. Then Gamma(1/2)=gamma; that's easy enough to remember. The area of a circle would be (gamma*r)^2. Redefine the Euclidean norm to include multiplication by gamma (R=gamma*r), and Area = R^2. Or, more generally, Vn=R^n/Gamma(n/2+1), and voila, no more stupid pi. Of course, this would make formulas for squares more complicated, but so what.
I love these Sunday Function posts, Matt! Thanks for taking the time to write them up. I'm more-or-less mathematically illiterate, but I can follow your descriptions and elucidations.
According to Wolfram Alpha ( http://www93.wolframalpha.com/input/?i=volume+of+an+n-sphere&a=*DPClash….\u0002n-.dflt-&a=*DPClash.GeometryP.volume-_*Volume- ), the n-volume is actually
       n/2  n
   2 pi    r
-----------------
  n Gamma(n/2)
http://en.wikipedia.org/wiki/Gamma_function#Main_definition
Gamma(n+1)=n*Gamma(n)
@dg
Ahah! I see! Thanks!
It's a little awkward that the "2-sphere" and "3-sphere" that you mentioned would actually be written as S^1 and S^2 respectively.
Sorry Dustron but gamma is already taken
http://mathworld.wolfram.com/Euler-MascheroniConstant.html
In particular it is -Gamma'(1).
Indeed these "volumes" go to zero as n increases, and they do so very rapidly. For n=50 the unit "sphere" has "volume" 1.7x10^(-13).
"Another funny fact about volume of N-dim. sphere with unit radius is that for N > 5 the volume actually starts to decrease with more dimensions."
Now that's interesting. Does it approach a minimum value? Surely it can't go to zero. That would just be wrong somehow. Must find time to play with this.
N-dimensional spheres trivially prove central management cannot succeed (unless it is exponentially tyrannical).
http://www.mazepath.com/uncleal/comprom.htm
@5
Non-integer volumes are used in Dimensional regularization in field theory as a tool for calculating the finite bits of divergent diagrams. It gets some use in condensed matter and nuclear theory.