I've been away from campus visiting family during the first part of the summer, in one of those rare confluences of events where research, classes, and teaching all find themselves on temporary hiatus. While it's pretty rare, I'm glad to take it. It is giving me Mathematica withdrawals though, especially with being able to easily make nice graphical plots and do some of the number-crunching I sometimes need for the more technical posts around here. Fortunately this is the last Sunday I'll have that problem, as I'll be back in Texas soon (and all those responsibilities will come roaring back). I'm looking forward to it.
For the moment I'd like to take this particular Sunday to kick off a Sunday Function project I've been thinking about for a while. Regular readers might recall the Greatest Physicists series here, and I'd like to do something similar with functions. Now obviously "Greatest Functions" is pretty much impossible. How could you even decide what counts as "one" function - are the exponential function and the trig functions different, or are they really different aspects of the same thing in complex analysis? What about polynomials and roots? I don't think a ranking of importance going to work.
But there's nothing stopping us from making a sort of Wonders of the World list for functions, unranked in any sense of "importance" but instead as a guide for tourists of mathematics to admire. Call it "10 Coolest Functions". So just like the Greatest Physicists, it's time to take nominations. Here's the guidelines:
1. If it's already been covered in Sunday Function, it's still perfectly fine. I could probably do dozens of posts on (say) the sine function alone.
2. Anything an undergraduate in any major might encounter is fine. Try to avoid very obscure and/or technically difficult functions.
3. Relevance in mathematical physics is not required, but preferred.
4. Sets of functions are fine, in contexts like Bessel functions or Legendre polynomials.
5. Pick your favorite 10 (or less), and rank them if you'd like.
Remember that this is a loose and fun exercise; a listing of favorites and subjective coolness rather than by "importance". You have lots of latitude, so if for instance you want to pick exponential/logarithm as one of your favorites that's fine.
Well it's a difficult task. But I know you're up to it!
- Log in to post comments
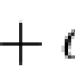


I like the general wave function y = A cos(xt + K) because it's so intuitive to relate the function to the real world.
The basic equation of motion x = x_0 + v_0 t + (at^2)/2 is my most used 'in real life'. I can't count the number of times I've been hiking, for example, and tossed a rock off a cliff to measure the height.
I don't fully understand all of these, but i know enough to know that they are completely awesome! (of course i would love to know more, that's one of the reason's i'm posting)
Euler's function is sooooo perfect (really useful too)
Hyperbolic functions (i know that they have some uses, but would love to know more about them.)
Gamma function
Riemann Zeta Function
Einstien Field equations (Maxwell's equations are great too.)
Fibonnaci equations.
I guess these are pretty typical (and i'm a little obsessed with infinite series); but they are still completely amazing to me since i'm only beginning to understand them.
e^iPi+1=0 no contest.
I'm a fan of the Dirac delta function and Chebyshev polynomials. However, I'd say that my favorite function is the simple linear polynomial. They're almost trivial to work with, but it amazes me how many disparate fields wind up using various forms of linear algebra to do really cool stuff.
It's been a looong time since my math classes at college, and I have forgotten the details, but I will never forget the Aha! feeling in the Hilbert Spaces class when I grokked how the Fourier Series was derived and why and how it worked. So something about Hilbert Spaces, eigenvectors, how the series functions all tie together. I think this is a similar requests to Watts' above, but maybe more meta.
Ooh ooh, imaginary numbers. I know they have a use, but I can't define one clearly.
sin and cos, together.
By way of computer graphics/simulations/games, they were my (and I would think many others') introduction to practical applications of trigonometric and/or transcedental functions, or for that matter mathematics of any sort beyond (+âÃ÷). To this day I think of coordinates, displacements, and vector components first and find the fondness for associating them with triangles weird. (âWhy are you introducing this complicated 'similar triangles'? It's obviously a linear interpolation.â)
f(θ) = eiθ is pretty and profound, but not so very practical and at-hand to the beginning programmer, and when I was young we were lucky to have floating-point numbers, let alone vectors or complex numbers. Ahem. </ramble>
Yeah, Delta function definitely comes in handy. Laguerre polynomials for quantum and optics. Hermite polynomials as well for laser physics. How 'bout Gaussian distribution functions? Where would we be without them? Ummm, step function, but that's almost the delta function. Fourier series, jeez how did I not put that one first? I guess it's not really a function, but related to them. Oh yeah, wavefuntion. That's semi-important. Well I can only think of 7 off the top of my head right now. Maybe I'll come back with more later. Thanks for doing this! I'm looking forward to the response.
The integral
the Fourier transform
Euler's totient function
prime counting function
the Schrodinger equation
isomorphisms
permutations
generating functions
the normal distribution (and the central limit theorem)
the wavefunction for the hydrogen atom (or even just spherical harmonics)
Why not smoosh all of these disparate polynomials into the hypergeometric and confluent hypergeometric functions.
I'm a fan of the mobius transfromation
f(z) = (Az+B)/(Cz+D)
Which you use to do isometries on the poincare model of hyperbolic space, among other things.
Are these to be functions or equations?
Whould you rather have the simple wave function count, or would we rather count the partial differntial wave equation?
Ideally we'll stick with functions, in the strict sense of a unique mapping of a domain onto a range. Most of the equations suggested are still fine, since they can be taken as functions or special cases of a function.
1. Arithmetico-geometric mean ! This is covered in the wonderful Borwein & Borwein book Â«Â Ï and the AGM ». (To use as a real-variable function, take AGM(1,x)).
2. Obviously, Riemann's ζ function. And an explanation of the whole concept of using functions to count things (think Weil conjectures).
3. WeierstraÃ' â function (and its differential equation that generates elliptic curves).
4. As a bonus, the whole Jacobi Î family of functions (these can be used to prove that every integer is the sum of four squares, and even to compute the number of such decompositions).
5. sin(x).
Well, to be more precise, Fourier series.
Well, to be even more precise, the example (given by Weierstraà if I remember well) of a real function everywhere continuous and nowhere derivable. And this is a welcome change from analytic functions ;-)
6. This is a doublet with ζ and Πfunctions, but generating series are great, too. They can be used to count partitions! They can be used to prove that if you have two d6's and the probability law for the sum of both is binomial, then both dice are actually fair ! They can compute the speed of algorithms !
7. Non-standard trigonometry: mostly hyperbolic trigonometry (easier than circular!) but also elliptic trigonometry (with fun Jacobi functions sn, cn and dn), or: elliptic curves done the old-fashioned way. (Nobody knows how to do this anymore...).
1. The exponential function (with or without complex argument), because it appears _everywhere_. It's one of the most important concepts in science.
2. The Gauss function, because of the central limit theorem. Everything complex enough is to some approximation distributed Gaussian.
3. Second degree polynomials, because so many thing can be modeled to some approximation as a harmonic oscillator with a parabolic potential.
4. The Fermi function, because of it's importance for statistical mechanics, and because it's an inspiration for optimisation algorithms.
5. The spherical harmonics are often useful when doing physics in three dimensions.
6. The Gamma function for it's nice mathematical properties and it's relation to the factorial.
7. The cycloid. Not very important, but cool and interesting.
8. The mexican hat potential V = -a x^2 + b x^4, because of the Higgs mechanism and it's intuitive explanation of spontaneous symmetry breaking.
9. 1/x, because of it's relation to ln(x).
10. x^x, because I'd like to understand it since the time someone mentioned it in school. Never found the time to.
11. Extra credits to the Dirac distribution. Not a function, strictyl speaking, but it's such a nice concept to work with when things are not continuous.
Addendum: the wonderful Book of Curves gets into drawing hyperbolics etc. E. H. Lockwood, available here as a pdf:
http://freebooksource.info/?p=38121
Almost all exercises for the reader. With pics goodness.
From high to low...
1. Ax = λx ... our friends the eigenvectors and eigenvalues sure do seem to pop up just about everywhere. I like it for its reductive properties on multidimensional data to get the "essence" of what's going on.
2. Fourier transform and its digital counterpart, the DFT. Some things are just too easy/hard to do in the time/frequency domain.
3. Logarithms! Would mighty Science (cap S) be where it is today if numbers had to actually be multiplied and divided? Could we have won the "good war" or got to the moon without the... slide rule?
Transforms... they're all good.
There is absolutely no contest: the coolest is analytically continued Riemann zeta function. Mathematicians also have some pretty neat functions, like the one to one onto mapping between 2^N and R. What can I say, I like bizarre more than useful.
Being an engineer, I prefer functions that are more useful and practical. One of the more useful functions I use is the Taylor series. It's simple. elegant, and yet provides very good approximations for even just a second-order Taylor. Not just for math, either; I've used the first-order Taylor to derive the equations of motion for a fluid particle, and this leads to the Navier-Stokes Equations that govern all of fluid dynamics.
It's amazing to me that such a simple mathematical "trick" like the Taylor series can lead to the formulation of (currently) unsolvable equations that have drastic real world implications.
You *could* do the Navier-Stokes Equations but this may be more trouble than it's worth.
In no particular order:
1. exp(z) for complex argument. Gives you the trigonometric and hyperbolic functions as well.
2. ln(z), the inverse of exp(z).
3. Bessel functions. If you deal with cylindrical geometry, these things pop up all over the place. Ditto if you are into magnetized plasmas, as I am.
4. The Haar wavelet. Basically a way of breaking a time series into sums and differences, with important signal processing applications. Invented about 70 years before anybody knew what a wavelet was. (Original reference: A. Haar, Zur Theorie der orthogonalen Funktionensysteme, Mathematische Annalen v.69 p.331, 1910.)
5. The Planck formula for predicting blackbody radiation. 'Nuff said.
6. Spherical harmonics. Useful, of course, in spherical geometries when you're dealing with not-quite-spherical functional dependences, like Earth's gravity or magnetic field.
7. The linear function. So much of physics, and other fields for that matter, consists of finding a best fit line passing through a forest of data points.
8. exp(-x^2), a.k.a. the Gaussian, which pops up all over the place.
9. Γ(x) and its relative, the factorial.
10. 1/r, the potential in three dimensions from a point source for a force which obeys the Laplace equation in the absence of sources.
I only have a few suggestions.
I would like the logarithmic spiral, and the hyperbolic sin/cos
All conic sections are solutions of the two-body problem. Planet's orbits are almost circular, long-period comets are very elliptical. Something nipping through a solar system is a hyperbola. Nice!
So I guess my function would be the polar form of the general conic equation.
Binomial coefficients.
Greens function.