All right ladies and gentlemen, take out your calculators. Punch in the number 4. Whack the square root button. What do you get?
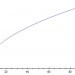
Unless I am badly mistaken, you're going to get the number 2. As you probably remember, the square of a number is just that number multiplied by itself: 3 squared gives 9, 4 squared gives 16, 1/2 squared gives 1/4, etc. The square root is the inverse of this process. It tells you what you have to square to get the given number. Two times two is four, so the square root of four is 2. You can plot the graph of the function to see what the square roots of various numbers are:
Now I invite you to try another experiment with your calculator. Type in negative 2 and multiply it by itself. Negative times negative is positive, and so you'll see that -2 * -2 = 4. So why isn't the square root of 4 equal to -2?
That's not even so bad. We can also define a 4th-root function, which tells us which number multiplied by itself four times gives us whatever we start with. For instance, the fourth root of 81 is 3, because 3*3*3*3 = 81. If you take the 4th root of the number 1, you'll see that the answer is 1, because 1 multiplied by itself four times gives you 1. But so does -1. And so does the number i. And so does the number -i. (The letter "i" is the symbol for the complex number which gives -1 when squared.)
What about 100th roots? It's more work, but there's in general one hundred 100th roots of whatever number you care to name. You can guess the pattern for the various other nth roots.
But there can be only one. A function can only associate a given number in the domain with one number in the range. We have to pick. The usual choice is to say that "the" nth root of x is the one that happens to be positive and real. This tends to be the most convenient and physically meaningful choice. It's not the only choice though, and our somewhat arbitrary selection of that (or any) particular choice will leave us with a gaping slice of discontinuous function on the complex plane. These slices are called branch cuts, and you have to deal with them carefully. We're smart people, we can do it. And one lovely Sunday sometime soon, we will.
- Log in to post comments

Dude, that was just a teaser!
Nitpicking, but 1/2 squared does not equal 1/2.
We teach people to take the positive square root 1) because its easier to teach and 2) because in easier topics in physics the real positive root often gives the right results. But that means you don't care about the information you're throwing away, cause you don't need the rest for the model you're using.
As soon as complex exponentials are useful (i.e., anything waves), for example, acoustic or electromagnetic or seismic propagation, the sign in square roots carries important information. Realistic modeling requires considering the medium and boundaries. Evanescent wave - perhaps you're trying to couple a signal into/out of a plasmon mode for transmission? Radio sounding of plasma - Landau damping? Resonance of a vibration?
1/2 square gives 1/2
eh?
okay, second to note it, but that stood out like a sore root.
"But there can be only one."
and that's why imaginary numbers equip themselves with swords and try to decapitate each other.
"But there can be only one."
You might want to look up multiple-valued functions.
De Moivre's formula for N Nth roots in the plane. But what about the volume?
Fixed the 1/4 typo.
Physioprof: Yeah, I know. ;) I was squeezed for time and so I decided to make this sort of a part-one intro to dealing with roots on the complex plane.
Re: multivalued functions. Strictly they're a contradiction in terms - really it's a shorthand for dealing with the more subtle concept on picking branch cuts and related matters.
The "square root" of a pure density matrix is a spinor. That is, given a spinor ket |a), we square it to make the pure density matrix by multiplying by the bra: |a)(a|.
This implies a square root function when one moves a pure density matrix to a spinor. In this case, instead of having an arbitrary sign, one ends up with an arbitrary phase.
Grumble. (Puts on curmudgeon hat.)
You are confusing the common name of a key on your calculator with a mathematical definition, as my mathematics colleagues regularly remind me when I use a term in a casual way.
The term "square root" is NOT the name for the "inverse of the process". A "square root" is a number (not "the" number, because it is not unique) that gives the desired value when squared. That means that -2 is a square root of 4, and for that reason the term does not define a (single-valued) function. Similar statements apply to Nth roots.
You are talking about the "principal square root", where one of the possible square roots is chosen - quite arbitrarily - so we have a well-defined inverse function. The key on your calculator returns the principal square root, which is only one of two possible solutions to the problem x^2 = 4.
This is not a picky detail when it comes to problem solving, because there are many problems where the principal root is not the correct answer. For example, spurious solutions need not be the negative ones. As noted by agm@3, this tends to be true only for easier problems.
PS -
When I looked to see if Wiki mentioned the distinction (it does), I found the first major error I've ever seen there. They claim that computers use logs to evaluate the principal square root function. This is wrong, unless designers have gotten stupid. They should use Newton's method, which is mega cycles faster.
You can't trust Wikipedia for math.
Their article on negative numbers tries to prove that a negative times a negative is positive.
But you can't prove that. It's a definition. Trying to prove a definition makes you lose credibility.
And the "proof" claims that multiplication is repeated addition. No it is not.
What a mess.
I believe this is a better way to answer the calculator question, but I'm not trying to make a big argument about it:
The square root symbol always represents the positive number whose square is the number under the square root symbol
Technically, the calculator is giving you a positive number because the symbol on the button requires the number to be positive.
Sorry for nit picking. :)
Robert: Their article on negative numbers tries to prove that a negative times a negative is positive. But you can't prove that. It's a definition.
It can be done by definition; on the other hand, it alternately can be proven as inference from more fundamental defining propositions, such as the nature of multiplication and the nature of additive inverses.
Anyone know offhand the canonical constructions for same from ZF and/or the Principia Mathematica?
In most textbooks the field (of which the real numbers are one example) axioms are:
addition and multiplication are associative, commutative, have distinct identities, and inverses (except 0 has no multiplicative inverse) and multiplication distributes over addition.
When talking about negative numbers you need to have an ordered field, which supplements the above axioms with the existence of a set P (called the positive numbers) which is closed under addition and multiplication and satisfies the law of trichotomy - for any x, x = 0 or x is in P or the opposite (ie additive inverse) of x is in P. A number is negative it its opposite is in P.
With these axioms you can indeed deduce (homework?) that the product of two negatives is positive.
Incidentally, an ordered field is still not enough to guarantee the existence of square roots (for example the rational numbers form an ordered field but contain no square root of 2). For that you need to add one additional axiom, completeness, which says that every nonempty subset which has an upper bound has a least upper bound.
Hey commentors at 10 and 11... stop complaining about wiki and fix it... it's really not that hard. Maybe not as much fun as just complaining about it though. Maybe more educational.
I'm afraid the Wikipedia article is unfixable. If I deleted the offending material then I would be accused of vandalism.
The article has a grain of truth in it. But then it goes off into three paragraphs based on multiplication being the same as repeated addition. This is a subtle issue. You can use multiplication to accomplish repeated addition in some cases, that is a fact. But you cannot define multiplication by saying it is repeated addition.
The "rule of signs" that makes multiplying a negative times a negative equal to a positive was adopted by mathematicians to be consistent with the distributive law of arithmetic. This is also a subtle issue. They were not required to make this rule, they did it because it makes mathematics more useful in solving problems. Therefore, it is only a rule because it is widely accepted.
But Wikipedia uses the word "requirement" to justify the law of signs and you will never understand math that way.
That's why you need to reference a rigorous mathematics book. You can get hopelessly confused on Wikipedia and not understand the truth.
#16 is Robert again. I forgot to add the name.
"The "rule of signs" that makes multiplying a negative times a negative equal to a positive was adopted by mathematicians to be consistent with the distributive law of arithmetic (emphasis added). This is also a subtle issue. They were not required to make this rule, they did it because it makes mathematics more useful in solving problems. Therefore, it is only a rule because it is widely accepted."
No ... they are required to make this rule if they want to keep the distributive law (and who wouldn't?) It's thought of as a rule, but it's actually a consequence (theorem) of the laws of arithmetic.
Incidentally the distribute law is why multiplication sometimes looks likes repeated addition ...
3 x 5 = (1 + 1 + 1) x 5 = 5 + 5 + 5
There was a desire by mathematicians to preserve the distributive law for negative numbers, but that is all you can say. Rigorous math books are careful to use and emphasize the word "desire" and they explicitly state that there was no requirement.
You are claiming that "to desire" is the same as "to require" if the desire is very strong, but that is just playing games with words. In the context of rigorous math, there is only one correct way to state the truth. If there were a requirement, then you could prove it, but you can't prove it.
Contrary to comment 13, the rule of signs is a theorem, proven as in comment 14; more generally in any ordered ring, i.e., with "positives" defined as members of a set P which is closed under addition, multiplication, and has the property that for every element a in the ring, either a or a' (the additive inverse of a) is in P.
In such a ring, considered as a Z-algebra, you have scalar multiplication by integers defined as 1 x a = a, a + a = 2a, etc. Also, 0 x a = 0, where the first zero is a scalar but the second is the zero element of the ring. (Easy to show.)
Then a' = a' + 0 = a' + (0 x a) = a' + ([1 + (-1)] x a) = a' + (1 x a) + ([-1] x a) = a' + a + ([-1] x a) = [-1] x a. So (-1) x a = a'.
Then it is obvious that for negative a', that is a' neither 0 nor in P, then a is positive, so a x a is positive, and then a' x a' = ([-1] x a) x ([-1] x a) = ([-1]x[-1]) x (a x a) =(1) x (a x a) = a x a. A prodigious use of the associative and distributive laws produces the Rule of Signs.
(Try proving the Law of Sines the same way?)
Steven Tesser: Contrary to comment 13, the rule of signs is a theorem
Actually, it was Robert in #11 who suggested it was just a definition; in #13, I was pointing out the alternative of taking it as a theorem/inference.
My main reference is "What is Mathematics?" by Courant, Robbins, and Stewart, plus a few other books that use similar language to explain why negative times negative is positive by definition and not by proof.
To be honest, I don't understand ordered rings, Z-algebra, and that other stuff, so I'll take your word on that.
All I know is that Courant et al. say that Euler tried to prove that negative times negative is positive, and Euler's proof was invalid. So they were really trying hard to emphasize that it can't be proved. They stated and restated that a few times.