Yesterday, as expected, severe underdog Texas A&M lost to #3 ranked Texas. Not as expected, the game was competitive right to the end, with an upset being threatened down to the final minutes. It was a great game to watch, with a final score of 45-35 - the highest total score in the history of the rivalry.
In this game as with pretty much all games at the college and pro level, the offense is very reliant on the forward pass. The quarterback picks a wide receiver, throws the ball, and with some luck the ball is caught for a gain. Now pretend you're filming such a pass on a video camera. From the time the football is let go to the time it's caught, it describes a trajectory that we can describe with some simple physics. We'll ignore air resistance, which is not such a bad approximation in football.
Now as you're playing the video of the pass, pause at some point on the trajectory. The ball appears frozen in the air. As you observe that instant in its flight, you know that the ball had a particular kinetic and potential energy. During the next frame the kinetic and potential energy will probably be slightly different as the ball changes position sightly. By carefully tracking the ball's position in each frame you could reconstruct the kinetic and potential energy of the ball in each frame of video. The kinetic energy is just the velocity squared times its mass mass divided by 2. The potential energy is just the height of the ball times its mass times the acceleration due to gravity.
Do this for each frame. Now each frame - in other words, each moment in time as the ball flies to its destination - is labeled with the kinetic and potential energy of the ball at that instant.
Now for the Lagrangian. For each frame, take the number for kinetic energy and subtract off the number for potential energy. That quantity is called the Lagrangian, named for Joseph Louis Lagrange. Why is this a useful thing to know? Weird as this Lagrangian sounds, it's actually part of a very powerful way to formulate classical mechanics. We do so in his day: take the value of the Lagrangian for each frame and multiply it by the duration of the frame (usually 1/30 of a second). Add all those up, and you'll end up with a final number called the classical action.
And here is the magic part. You can think of an infinite number of strange and bizarre curved or looped or whatever trajectories that the football might have taken other than the one it did. You can imagine calculating the action for any of those imaginary trajectories. But here is what you will find. The action that results from the actual motion is the smallest possible value for any trajectory. Any other path, with any other weird changes in speed or elevation, will produce a higher value of the action.
This statement is frequently called the principle of least action, and it's also known as Hamilton's principle (after the Irish physicist William Rowan Hamilton). If you want to know about a trajectory, it's possible to use a technique in the calculus of variations to find the trajectory from that principle. Since the action is purely a scalar quantity involving energy, we don't have to worry about the frequently difficult vector character of Newton's force-based method of doing mechanics. It's a neat little bit of physics sorcery.
[Note for the technically inclined: Formally we're looking for a stationary action, not truly the least action. Hamilton's principle itself doesn't preclude the stationary point being a maximum, though in practice this is not a problem.]
- Log in to post comments

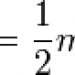
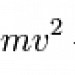
Consider two footballs pursuing local parallel-displaced minimum action paths whose vacuum free fall accelerations were identical in direction and divergent in magnitude. Reduce that to practice.
Physics postulates isotropic vacuum. Conservation of angular momentum is Noether's theorems contingent - powerful validation including quantum mechanics. EM, polarized EM, and individual massed particles propagate through hundreds to billions of lightyears pathlengths without refraction, dispersion, or gyrotropy. Is theoretic compliance with prior observation airtight?
Nope. The boojum is an extrinsic property with an emergent scale: chiral vacuum background (e.g, a pseudoscalar field) acting only in the massed sector upon chemically and macroscopically identical (e.g., solid single crystal footballs) opposite geometric parity atomic mass distributions. Enantiomorphic space groups P3(1) (right-handed) and P3(2) (left-handed): glycine gamma-polymorph. P3(1)21 (right-handed) and P3(2)21 (left-handed): quartz, cinnabar, tellurium; berlinite and analogues.
A sock cannot identify feet. A left shoe cannot identify a left foot, but a right foot is anomalous. Paired enantiomorphic footballs would left-footed vacuum background free fall with different insertion energies and different vacuum "viscosities" (no privileged direction). Physical theory then requires a fundamental rewrite from an unsuspected footnote, yet no prior observation would be contradicted, General Relativity to quantum field theory.
http://www.mazepath.com/uncleal/erotor1.jpg
Do the experiment.
I have known this since grad school, but only in the sense in the sense that I can follow the mathematics. But I have never been able to wrap my head around the concept of what exactly a Lagrangian is. The classical Hamiltonian can correspond to the total mechanical energy, and that's sits just fine, but what does the Lagrangian really tell us? I would love to see a simple mechanical model where the Lagrangian corresponds to something tangible. Anyone?
The reason why the max/min distinction is not a problem is because a maximum in the action is an equally valid path to a minimum. The reason? Look no further than the path integral approach to quantum mechanics - the paths that suffer the least destructive interference from nearest neighbors are those that are at or very close to stationary points.
Where do you get the Lagrangian from in the first place?
I get it that T-V comes from some notion of 'virtual work', and the Einstein Hilbert action comes from the minimum path length through curved space time.
What about the others, like the -1/4 F_munu F^munu in electrodynamics? Do they work backwards from Maxwell's equations until they get an action that produces them?
Matt your essays should be put into a book. I think they would help a lot of students understand things more clearly than the traditional teaching mechanism. This essay for example helps me recall the lagrangian I learned about 39 years ago in mechanics. Imagine how it would help and motivate a student learning the subject today.
Hold on, how did Lagrange find that out? It seems quiet unintuitive for me. And what is so special about K-U?
That game was awesome! I had no idea a person could reconstruct a kinetic energy model frame by frame. That's really interesting.
Great post! One of our professors was discussing about this in one of his classes. I am a college sophomore with a dual major in Physics and Mathematics @ University of Canterbury in Christchurch, New Zealand. By the way, i came across these excellentphysics flash cards. Its also a great initiative by the FunnelBrain team. Amazing!!!
But the true question is, of course, WHODAT!