Pretty much every high school student can quote the formula for the area of a circle: it's A = pi r^2, where r is the radius. Most of them can do the same thing for the volume of a sphere: V = 4/3 pi r^3.
You could, if you wanted, generalize the concept and call circles "2-spheres", because they're the set of all points a given distance from the center in a 2d space. A sphere would be a "3-sphere", because it's the set of all points a given distance from the center in 3d space. A "1-sphere" would be the set of all points on a line equidistant from the center on a line. Of course there could only be two of them, and so the "volume" of a 1-sphere would be V = 2r. So we'll scrap all the different words for these spheres and just call them n-spheres, and we'll call the content of their interior the "volume", even though in 2d (for instance) we might usually call it the area.
Now that we have volume formulas for n = 1,2,3, we might want to find the volume of higher-dimensional spheres. There's plenty of abstract interest in the result, but there's also plenty of use in physics for this - very often we describe phenomena in terms of phase space, which might include parameters like momentum. Each parameter is a dimension, and so though there's not literally 100 spatial dimensions, the mathematics is still just as useful in a formal setting for describing those parameters.
Now we actually have to calculate the volumes. There's a few ways to do it; we'll take the "easy" trick way. From scratch, we know that the volume has to be proportional to the nth power of the radius for dimensional reasons. The only question is the constant in front of that radius. As such, we can write down the volume as a function (our Sunday Function) of r, modulo that constant:

This is a volume, so we expect we might have to integrate at some point. Might as well write down the differential now:

Now we start working on the trick. I have no idea who thought of it first, but it's pretty clever. Essentially, we start with a very standard Gaussian integral and bootstrap our way backwards. So write down that Gaussian integral:

Now multiply it by itself n times. To keep track of all the different x's, we'll subscript each one of them with an i:

Yeesh. It looks a little ugly, but it appears pretty straightforwardly by the rules for multiplication of exponents. e^a times e^b = e^(a + b), etc. However, this lets us make two dramatic simplifications. The sum in the exponent is just r^2, essentially because the Pythagorean theorem works in higher dimensions. The product of the differentials is just the differential volume element, which we worked out above. So swap those facts in:

Cn is a constant, it can be pulled outside of the integral. Then the integral can be done (or looked up in a table). Its solution is in terms of the Gamma function:

Which we can recast in terms of the factorial function and solve for Cn:

Plugged into our original formula, and we have the volume of an n-dimensional sphere:

If we plug in n = 1-3, we get the constants we expect. We can also work out the volume of the next few higher dimensions just for fun:
4-volume: (1/2)π2r4
5-volume: (8/15)π2r5
6-volume: (1/6)π3r6
I don't expect school kids will be memorizing those any time soon. But it's cool to be able to tell them that we have figured those higher dimensions out if they ever need them.
- Log in to post comments

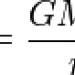

I remember learning about this in calculus, although the method we used was recursive to find this formula.
You didn't mention a 0-sphere. I think it's interesting that it has a volume of 1. I don't usually think of a point as containing volume, but that's what the formula says.
And of course the formula for the surface area immediately follows: it's dV_n/dr. Which gives the expected answers for n=1,2,3: 2, 2πr, and 4πr^2, respectively.
Kyle: The problem with your argument is that in the course of the derivation there is a division by n. So the volume of a 0-sphere is undefined. Its surface area, however, is what you would expect: 0.
Computing microcanonical partition functions?
Sure enough, that's the context in which I originally learned this. This particular derivation is in the appendix of Pathria's book on statistical mechanics. However, he doesn't specify who originated it - perhaps it's just one of those things that's been around forever.
No worries about division by zero, 0! = 1 by definition.
There is another point where the hyper-volume is equal to 1 as well as for n = 0. =)
It's worth noting that this is the volume of the n-sphere in n dimensions. The volume of the 2-sphere in 3 dimensions is zero.
It's interesting that as the n goes to infinity, the n-dimensional content of the hypersphere goes to zero.
What about when n = infinity? Then the analysis in this post is no longer valid since there is no non-zero translationally-invariant measure which assigns finite volume to any open sets. Since the zero measure is trivial, I tend to think of the volume of the infinite-dimensional unit sphere as infinite, although it does not matter / is undefined.
@ijc: I wouldn't necessarily jump the gun on the volume of that infinite-dimensional sphere being infinite. I would imagine the closest parallel would be a volume measurement in L2-space, i.e. the "volume" (if it exists) of the set of L2-square integrable functions s.t. their self inner product <= r... but this stretches my math knowledge.
But I get your point; something about dimension doesn't work at this point, right? I mean, if we're talking about Hausdorff dimension, that means that when the diameter of a (compact?) space is magnified by c then the volume will multiply by c^(dimension)... this would be meaningless in an infinite dimension, regardless of whether or not we're talking about a countable or uncountable dimension.
Makes me want to open my topology books again. :D
Kyle, Eric: Actually, I think it's undefined due to V=1*0^0, r=n=0. At least, that's what I think r should be if n=0.
Matt: The steps are clear, but why did we select the Gaussian integral to begin with?
This makes me want to do some technology studies.
Abu: The Gaussian integral trick is a way to convert from Cartesian to n-spherical coordinates and give us a shortcut for evaluating the angular integrations. You may recall (at least this is how I learned it) that the reverse of this trick lets you calculate the Gaussian integral analytically: we know how to do the angular integration in the n=2 case, and the coordinate conversion maps dx dy into r dr dθ which makes the integrand doable analytically.
Can we talk about the gamma function sometime? 1.5! is hurting my brain.
http://en.wikipedia.org/wiki/Sphere
A circle is not a 2-sphere.
Consider the ratio of volumes of an N-cube with an inscribed N-sphere. As the number of dimensions N increases, the fractional volume occupied by the N-sphere rapidly asymptotes toward zero. This is a remarkably powerful proof that centralized management cannot create functional decisions,
http://www.mazepath.com/uncleal/comprom.htm
How do non-integer factorials work?
For those curious about non-integer factorials, the answer is the Gamma function. It was a Sunday Function a while back.
It may be again. You may notice that the powers of pi don't increase 1-to-1 with n, implying that the half-integer factorials are spitting out factors of pi. The reason for this is interesting, and we ought to take a look at it eventually.
Ok, I got a question. What happens to the radius of the sphere with unit volume as the number of dimensions goes to infinity?
ppnl, Any ball with a finite volume has to have an infinite radius in a space with infinite number of dimensions.
A hand waving explanation is that in order for something to have a finite volume, it must have some finite extension to every single dimension. For example, a two dimensional plane has zero three dimensional volume, and a three dimensional cube has zero 4-volume. For something to have infinite-volume, it has to extend to infinitely many dimensions. But a ball that extends to an infinite number of dimensions has to have an infinite radius, since for a ball r^2 is proportional to the square of the number of dimensions, which is infinite.
ppni - Infinity. If you set V = 1 and solve for r you get
r=((n/2)!/pi^(n/2))^(1/n)
The factorial in the numerator grows faster with n than the power in the denominator and the 1/n power can shrink it. Factorials grow faster than powers..
*not a rigorous proof
thanks..i really learned a lot from this blog..
thanks for the info! :]