Well, last time we were looking about the classical probability density for a bouncing ball, and the quantum mechanical probability distribution for the same. They looked not even a little bit alike. This is kind of a problem, since we know from experience that classical physics works pretty well, and from more modern work we know quantum mechanics works pretty well also.
However, despite their apparent inconsistency it turns out that we're just not looking close enough. The quantum nature of things is usually (though not quite always) apparent when the energy level of the system in question is similar in size to the size of the quantum jumps. Most of the time these quantum jumps are very, very small in comparison to the energy of macroscopic objects such as, say, a dropped baseball. For instance, the ground state of a baseball in the 9.8 m/s^2 gravitational field of the earth is something like 0.0006 eV, which is just tiny. A baseball dropped from 1 meter will have an energy of around 1.4 joules, which is about a whopping 10^22 times larger. It's really no shock that the quantum nature of the ball isn't visible - assuming that quantum mechanics really does look like classical mechanics for large quantum numbers.
Does it? Here's the n = 1 probability distribution compared to the classical one (axis scales are arbitrary [Though see discussion in comments - Matt]):

They don't look much alike. In fact, there's a finite probability to find the particle actually higher than the classical limit imposed by E = mgh. Try the n = 5:

Well, they still don't look much alike. There's still some portion of the quantum distribution above the classical turnng point, but less. And if you squint, the lumps in the quantum distribution look sort of like the smooth classical one if you take an average.
But we're at small quantum numbers yet. Try n = 50. The portion that sticks out too far is much smaller in comparison, and those bumps are looking pretty hard to distinguish from the smooth classical curve.

Extend this to n = 10^22 or so and it's starts to look pretty plausible that the classical and quantum distributions are indistinguishable to the naked eye. This is called the correspondence principle, which basically says that the quantum mechanical answer will arbitrarily approach the classical answer for large quantum numbers. As it happens, that principle doesn't quite save us all time time. There are quantum systems where large quantum numbers are not really possible - the spin of silver atoms coming out of a Stern-Gerlach device, for instance. But that's usually not to much of an issue.
- Log in to post comments
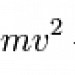

How come you don't label your axes? I have no idea what the graphs are supposed to represent.
let's not point Matt's wife at xkcd...
Nice demonstration of why newton works at the scales of ordinary life. Or in other words why a Basketball player does not have to worry about quantum mechanics when making a shot.
They are clearly labeled just above the first graph as totally arbitrary. ;)
Actually they're not though, the x-axis is in units of (hbar^2 / (2gm^2))^(1/3). For a baseball this is about 1.4e-23 meters - less than a millionth of the diameter of a proton. Y-axis is normalized probability/length, with the same length units.
none of this makes any sense
can some1 help me read this??
ok, i'm leaving now! this is a stupid site.
Nice demonstration of why newton works at the scales of ordinary life. Or in other words why a Basketball player does not have to worry about quantum mechanics when making a shot.