Sunday Chess Problem

This week's problem was composed by Mircea Manolescu in 1956. In the position below, it is white to move and mate in two.

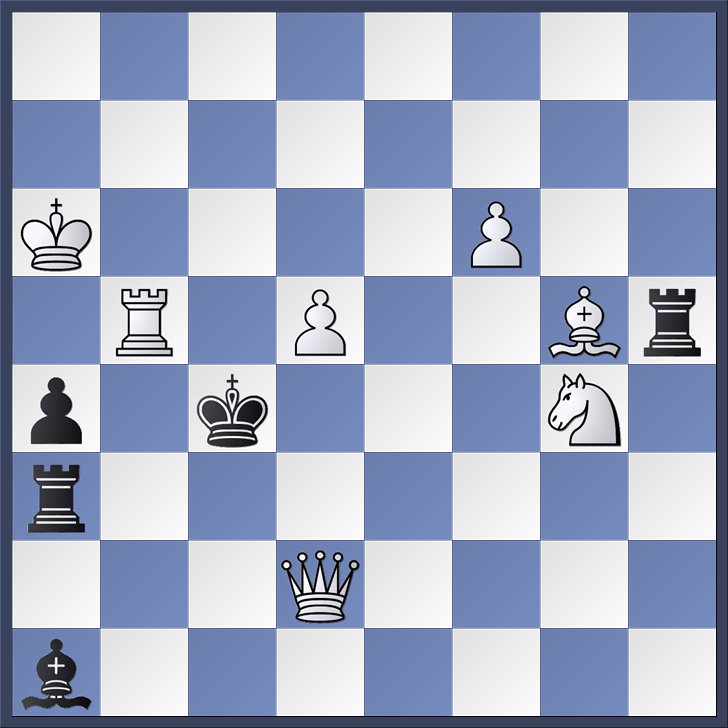
Remember that white is always moving up the board, while black is always moving down. Vertical files are labeled as a--h from left to right, while the horizontal ranks are labeled 1--8 from bottom to top. So in the diagram we see that the white king is on a6 while the black king is on c4. When we write down moves, an “x” indicates a capture.

This problem is our first example of a multi-phase problem. To understand what that means, have another look at last week's problem. There we introduced the Grimshaw, which refers to a situation in which two pieces of the same color, usually a rook and a bishop, interfere with each other on the same square. Notice, though, the structure of the problem. White played his key move, and then produced some pretty mates in reply to black's various replies.

It was a very nice problem, but there is only so much play you can pack into such a scheme. To enhance the strategic richness of the problem, composers will typically strive to include several phases in their problems.

Imagine that it was black to move in the diagram position. If black, for some reason, was to play 1. ... Bc3, then white could mate with 2. Ne3 mate.

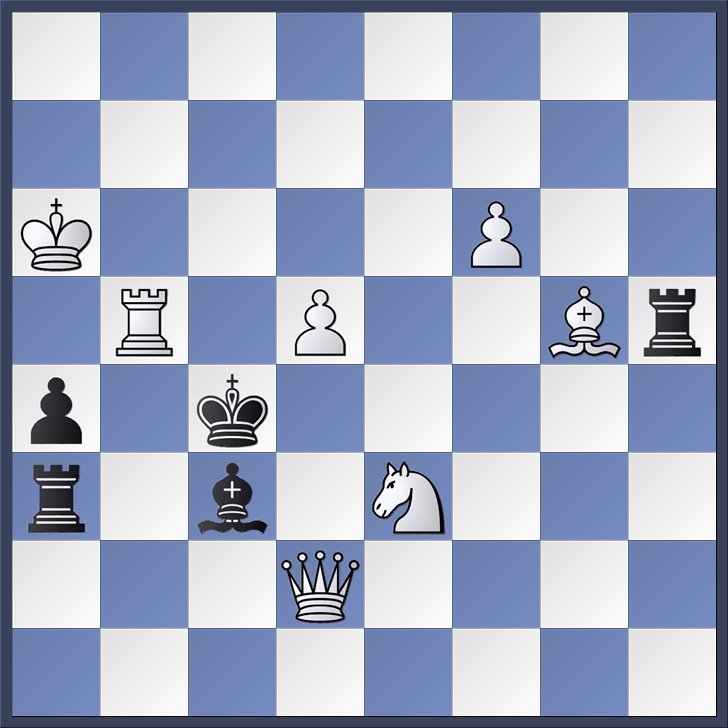
On the other hand, if black were to play 1. ... Rc3, then white could mate with 2. Ne5 mate.

These two lines are referred to as the set-play. We see that white is prepared for a potential black Grimshaw on c3.

But we still need to find the key move that will allow white to give checkmate in two moves. So white might try 1. Nf2. This move messes up the two set mates we have already seen. It does, however, place an extra guard on d3. White is therefore threatening 2. Qb4 mate. Interestingly, black's Grimshaw moves on c3 defend by closing the white queen's path to b4. White now has two new mates for those moves. We get the variations 1. ... Bc3 2. Qd3 mate.

And 1. ... Rc3 2. Qf4 mate.

Mission accomplished? Not quite. White has no mate after the simple defense 1. ... Rb3.

Moves like 1. Nf2, which fail only to a single black defense, are referred to as tries. Some problems will work in multiple tries to enhance the strategic content of the problem. The set-play and try-play together are often referred to as the virtual play.

The actual play begins with the key move 1. Be3!

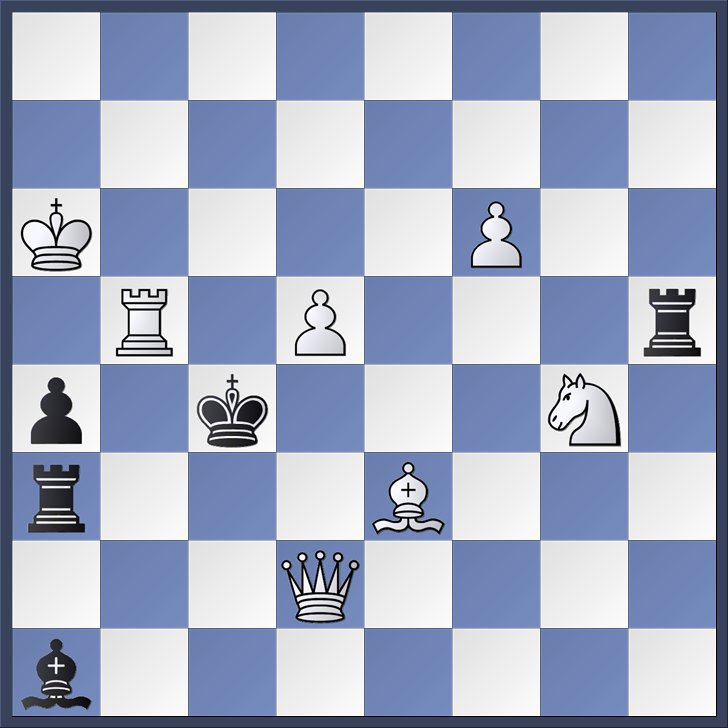
This puts an extra guard on c5, thereby allowing white to threaten 2. Rb4 mate. Black's Grimshaw moves on c3 again defend by cutting off the white queen, meaning the white rook will be unprotected on b4. Neither the set mates nor the try mates will work anymore (you should verify this for yourself), but white picks up yet another two mates in response to the Grimshaw. We have 1. ... Bc3 2. Qe2 mate.

And 1. ... Rc3 2. Qd4 mate.

There is also some by-play, which we include for completeness: 1. ... Rb3 2. Rc5 mate and 1. ... Rxe3 2. Nxe3 mate.

So, we see changed play across three phases in response to a black Grimshaw on c3. This sort of scheme, in which white has different responses to the same black defenses across at least three phases is referred to as a Zagoruyko (after the great Russian composer Leonid Zagoruyko).

Great stuff! Composers have been ingenious at extending the basic Zagoruyko scheme to include more than three phases (through the addition of extra tries) and more than two black defenses, but that shall have to wait for another week. See you next Sunday!