Posted by By way of Observational Epidemiology, we find an interesting NY Times article by Michael Winerip describing a seventh grade teacher’s experience with value added testing in New York City. I’ll get to value added testing in a bit, but the story also highlights why we need more reporters who have backgrounds in math and science. Winerip:
On the surface the report seems straightforward. Ms. Isaacson’s students had a prior proficiency score of 3.57. Her students were predicted to get a 3.69 — based on the scores of comparable students around the city. Her students actually scored 3.63. So Ms. Isaacson’s value added is 3.63-3.69.
What you would think this means is that Ms. Isaacson’s students averaged 3.57 on the test the year before; they were predicted to average 3.69 this year; they actually averaged 3.63, giving her a value added of 0.06 below zero.
Wrong.
These are not averages. For example, the department defines Ms. Isaacson’s 3.57 prior proficiency as “the average prior year proficiency rating of the students who contribute to a teacher’s value added score.”
Right.
The calculation for Ms. Isaacson’s 3.69 predicted score is even more daunting. It is based on 32 variables — including whether a student was “retained in grade before pretest year” and whether a student is “new to city in pretest or post-test year.”
Those 32 variables are plugged into a statistical model that looks like one of those equations that in “Good Will Hunting” only Matt Damon was capable of solving.
The process appears transparent, but it is clear as mud, even for smart lay people like teachers, principals and — I hesitate to say this — journalists.
What’s freaking Winerip out? This:
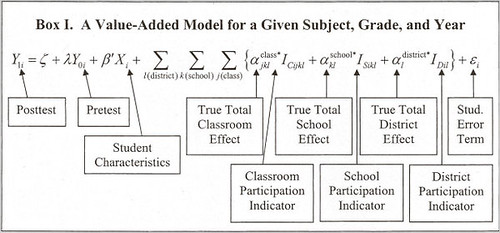
AAAIIIEEEEE!!!!
If the journalist in question is unable to understand linear regression, then maybe said journalist shouldn’t be reporting the story. Given the importance of understanding the method–and its flaws–a statistically literate reporter is essential for this story, although Nate Silver can’t do everything, I suppose.
If you have the training, it’s not hard to understand at all (and if our elite finishing schools actually educated most of their students, they should be able to understand this). Sadly, many of our elite journalists are out of their depth when the math moves beyond arithmetic. A good newspaper would hire an art critic with knowledge of the subject, so why not here too? Mathematics is a skill, not magic.
It’s too bad, since understanding what happened to the teacher Winerip covers, Stacey Issacson, is really critical. In NYC, student achievement, based on an exam, is classifed into four levels, 1-4 (and, no, membership in each category doesn’t scale linearly[LA times]). The average score for each teacher is then calculated. Using the scary formula above, the school administration can then gauge (supposedly) how effective the teacher is. Issacson, who teaches at an elite school, has 65 out of 66 students meet standards (a score of 3 or 4), with an average of 3.63. If she performed at the average level (50th percentile) her students should have had a score of 3.69.
Andrew Gelman breaks down the numbers using that complex tool known as algebra and identifies the difference between between a score where Issacson would have received tenure versus a failing teacher (7th percentile): failure is 43 “4s” and 22 “3s” while average, tenure granting peformance is 47 “4s” and 18 “3s”. Basically, the difference is four kids doing a little better on an exam (in the worst case, one could have four students right at the edge). Does anyone believe that this is a real difference? Anyone who has ever taught at any educational level? Winerip correctly notes that there’s a lack of precision around this estimate:
Moreover, as the city indicates on the data reports, there is a large margin of error. So Ms. Isaacson’s 7th percentile could actually be as low as zero or as high as the 52nd percentile — a score that could have earned her tenure.
So, basically, we have ‘progressives‘ lauding a teacher evaluation method (“measurable differences”) that can’t really measure if a teacher is doing a good job. The method works great, except that it can’t tell if you’re succeeding or failing.
Yet teachers–and not the politicians, adminstrators, and ignorant pundits who support these foolish policies–are the problem.
In light of these inaccurate guestimates, teachers have every right to be angry about education ‘reform.’
A statistical aside: The method above assumes linearity– a * I. That’s fine if you’re trying to establish a general pattern, but if you’re trying to accurately predict what should happen and minimize the residual, you probably need a more complex ‘link function.’
March 15, 2011
March 15, 2011
March 15, 2011
March 15, 2011
March 15, 2011
March 15, 2011
March 15, 2011
March 15, 2011
March 18, 2011
but even I can tell that it is an attempt to give the appearance of measuring precisely something that cannot be measured precisely. “Politicians, administrators, and ignorant pundits” likely know that it is bs, but want to cover their own behinds and save their own bloated salaries.