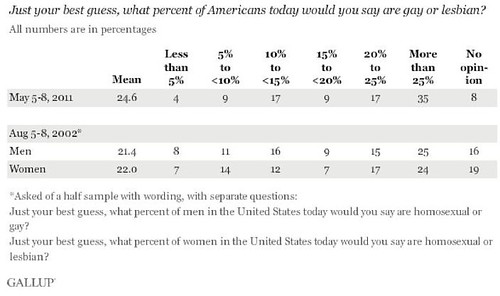
...don't understand fractions. A recent Gallup poll asked people what percentage of Americans were gay and lesbian. The results? 52 percent estimated that twenty percent or more of the population is gay or lesbian:
Keep in mind that most estimates put the lesbian and gay population at around three percent. While the Gallup pollsters and other commentators ascribe this to increasing acceptance, I think it's something more basic--a lot of people don't really instinctively make the link between fractions and percentages:
The arithmetic gap is the most obvious one: profs over a certain age (and some immigrant profs) were drilled in mental math; Canadian students under a certain age haven't been. Some implications of the arithmetic gap are familiar: profs who can't understand why students insist on using calculators; students who can't understand why their profs are so unreasonable.But the mental arithmetic gap has more subtle implications. Mental calculations often require intuition about, and comfort with, the use of fractions. Pre-calculator: 1/3+1/3=2/3. Calculator era: 0.3333....+0.3333....=0.6666.... Pre-calculator: "To multiply by twenty-five, divide by four and add two zeros (25*Y=1/4*100*Y)" Calculator: Multiply by twenty-five. Back in the day, fractions were easier than - or at least not much more difficult than - decimals. Calculators make fractions obsolete.
I think the answers would have been much more reasonable--keep in mind one of out three respondents thought 25% or more of the U.S. is gay or lesbian--had the question been asked in terms of fractions. It's a lot easier to think, "I know X gay people out of Y" and answer that question directly than transform it to percentages--some people aren't good at doing long division in their heads. If you look at how various demographic groups answered, the less educated and poorer respondents had much higher estimates of the gay and lesbian percentage of the population. Younger respondents also scored had much higher estimates; if Frances Woolley is correct, this shouldn't be surprising either.
I think this odd result might have something to do with the way the question is phrased.
An aside: My guess if you asked people about American Jews, we would also be ridiculously overestimated (we're about two percent of population, depending on how exactly one does the counting). I think once a minority is no longer denigrated or invisible (and those two states are related), that combined with a cognitive bias against choosing extremely high or low frequencies would yield overestimates. That still doesn't explain so many people believing one out of five or more Americans are gay or lesbian...
- Log in to post comments

If one believes that there is some sort of homosexual conspiracy going on (against marriage? or prayers in school? traditional manliness?) it would help to also believe that there are large numbers of teh gays out there doing the conspiring. "50% of the population is gay and they're all out to get me!"
From what I have read (some years back) people do best if they have to guess integers. So this kind of question might be phrased like this:
Suppose that you have a cross section of 1,000 American adults. How many do you think are attracted exclusively to their own sex?
Perhaps one reason for the high percentages is a belief that having even one consensual same sex experience means that you are gay or lesbian. Something like the one drop rule for being Black.
The fear of the Other drives the over-estimation of minority groups. Math skills are just hurt by the panic that follows. If 1/4 of the population is gay and another 1/4 is Jewish and there are more Blacks than those two groups put together, it's pretty lonely and frightening for the normals. Who has time to worry about their innumeracy then?
I would have said 10%
could the problem just be definitional?
Most of the studies show rates of 'homosexuality' (self-described) at around 3%, but same-sex attraction at 20+%
maybe respondants are not too far off? A lot of people would say someone attracted to the same gender is 'gay', rightly or wrongly (wrongly!)
I would lean towards a mix of fear and publicity in honesty. It is probably largely the "hear one person say the same thing 20 times and your brain registers 20 people holding the same belief" thing
The inability to transpose fractions and percentages is probably related to the failure to think critically. I bet if you asked those people what 20% *means*, they would be able to tell you, as a fraction. But it doesn't occur to many people, on their own, to think that way.
The fractions vs. percentages issue may be a factor, but I think it is more likely that people in general massively overestimate such figures. Their perception is driven by Availability Bias / Social Amplification. We talk more often and freely about LGBT today even compared to 2011, more people have come out of the closet, etc.
Personally, I would have guessed 10%, much like Fred above, just based on my own environment, but obviously it is not representative.