![]() So, it's been a while, but let's see if we can't hit the ground running with a good physics post. There have been a few notable physics events since I went on hiatus, but for a return to physics ResearchBlogging, we'll go with something near and dear to my heart, ultracold atoms. Specifically, this Science paper (free arxiv version) about passing atoms through a narrow channel. This is a cool bit of subfield-crossing physics, so let's dust off the Q&A format, and go through it.
So, it's been a while, but let's see if we can't hit the ground running with a good physics post. There have been a few notable physics events since I went on hiatus, but for a return to physics ResearchBlogging, we'll go with something near and dear to my heart, ultracold atoms. Specifically, this Science paper (free arxiv version) about passing atoms through a narrow channel. This is a cool bit of subfield-crossing physics, so let's dust off the Q&A format, and go through it.
Hey, dude, long time no see. So, what's the deal with this paper? Well, the title pretty much tells you what's happening. They're looking at the behavior of ultracold atoms passing through a tiny little channel between two reservoirs of atoms. This is directly analogous to the behavior of electrons passing down a thin wire, but the cold-atom system gives you really nice control of the parameters involved, and lets you see some slightly surprising things.
OK, back up-- atoms are like electrons? How do you figure? They're not obviously identical to electrons in that they're not charged, but a properly prepared sample of the right kind of ultracold atoms can look very much like a sample of electrons inside a solid. In this case, they've chosen lithium-6 atoms, which belong to a class of particles called "fermions," which have the property of being antisocial-- no two of them can be in the same state. Electrons are also fermions, and when you cool the sample of atoms down far enough, the distribution of energies of the atoms looks like the distribution of energies of electrons inside a metal.
How cold are we talking, here? Their operating temperature is around 250 nanokelvin (250 billionths of a degree above absolute zero), though the more important figure is the temperature as a function of the Fermi energy, which is, roughly speaking, the energy of the last atom added. In those terms, the temperature is 0.36 times the Fermi temperature, so a respectable distance below it.
Wait a minute, how can the temperature be lower then the energy of the last atom added? I thought temperature measured the energy of the atoms? Technically, the temperature is related to the spread in the energies of the atoms. For a hot gas of ordinary particles, it doesn't make much difference, but you can create systems where the temperature is very low but the average energy is high. Think of launching a cold bottle of gas into space in a rocket: all of the individual atoms in the bottle have a large energy according to somebody on the ground, because they're all flying in the direction they were just shot. You wouldn't say that the gas was hot, though, because the spread in the energies of the atoms isn't very large, and the bottle would still feel cold to somebody inside the rocket.
OK, but then what's the deal with the temperature and the Fermi thingy? The Fermi energy is a property of a collection of fermions that comes about because of their antisocial nature. If you try to pack a whole bunch of fermions into a box, you have to abide by the Pauli exclusion principle, which says that no two fermions can occupy the same state (which itself is a consequence of the rotation symmetry of fermions, but that's a whole other blog post with cute toddler video). Quantum physics tells us that the particles in the box can only have certain energies, integer multiples of some characteristic energy determined by the size and shape of the box. Each particle you stick in the box takes up one of these allowed energy states, generally starting with the lowest possible energy. As you stick more of them in, each has to go into a higher energy than the one before it.
So, it's like electrons in an atom? Right. If you've ever taken a basic chemistry class, you talk about electrons "filling up" energy "shells" in the atom, and the number of electrons in the final shell determines the reaction properties of the element in question. This is the same sort of thing, only the Fermi energy is a characteristic of the whole box full of particles.
And because it's a cold system, there isn't much uncertainty about those energies? Right, at least loosely speaking. At absolute zero, you would expect one particle for every energy state below the Fermi energy, and no particles with energies above the Fermi energy. If the temperature is greater than absolute zero, though, as it is for any real system, there's a little fuzziness to the boundary-- you'll find a few empty states below the Fermi energy, and a few particles with energies above it. The temperature basically tells you how wide that fuzzy band is-- in this case, you'll find some empty states down to about two-thirds of the Fermi energy, and a few particles with energies up to about one-and-a-third times the Fermi energy.
And this whole excessively long introduction was to establish that this is what you see in a metal? Um, yeah. Got a little carried away, there. I'm out of practice.
Anyway, yes, this distribution of electrons looks very much like what you see for electrons in a metal. So, if you've got a bunch of these super-cold atoms, you can describe them with the same techniques used to describe electrons in a solid.
And the advantage of this is..? Cleanliness, basically. The atoms behave like electrons in a mathematical sense, but they have a number of advantages. First, they're not charged particles, so they're less sensitive to random perturbations in the local environment, which means you don't have to work at the bottom of a dilution refrigerator with samples made in a clean room. The atoms also have discrete internal energy states that let you detect them with high efficiency by looking at what frequencies of light they absorb and emit. And finally, the atoms can be freely floating in space, with the role of the confining solid played by lasers and magnetic fields you apply in the lab, which means you can look at them while they're "inside" the "solid" in a way that's extremely difficult to do with real electrons inside real solids.
OK, so they're using hugely complicated apparatus to simulate solids that you could walk outside and pick up. Got it. What did they measure with this? Well, in this case, they measured something really simple that is extremely difficult to measure in real solids, but provides a surprisingly rich system to study: they looked at the flow of "electrons" through a narrow "wire."
So, they stuck a wire into their cold atoms? No, they used a laser to simulate a wire. They made one big cloud of atoms, then stuck in a laser beam that blew away all the atoms in its path, splitting the cloud into two. The laser had a slight imperfection, though-- a narrow "shadow" in the center of the beam, where atoms weren't blown away, which then acted as a thin channel connecting the two regions.
And they get atoms to flow across this, how? Well, if they apply a small magnetic field gradient during the process of making their ultracold atoms, they can get a lopsided cloud, with about 20% more atoms on one side of the channel than the other. It looks like this:
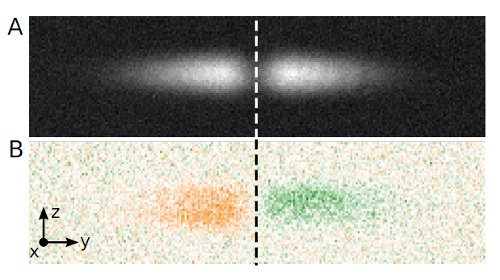
Top: the atom cloud; Bottom: false-color image with orange indicating an excess of atoms and green a lack.
The top (black-and-white) image is a picture of the cloud with a slight imbalance. The difference between the two sides isn't immediately obvious, though, so the bottom picture shows a false-color rendering, taking the difference between a cloud with an imbalance between the two sides and one with the same number of atoms on each side. Orange indicates an excess of atoms over the equally-split cloud, and green a lack of atoms compared to the equally-split cloud.
Once they've got that imbalance, they just turn the magnetic field off. At which point, the atoms want to flow from one side to the other until the numbers are equal. They can monitor this flow by taking successive pictures of the cloud, and track the flow that way.
So, the two clouds are the poles of a battery, and the channel is a wire between them? It's more like a capacitor than a battery, because there's a big imbalance at the start, that decreases exponentially. The results are shown in this graph:
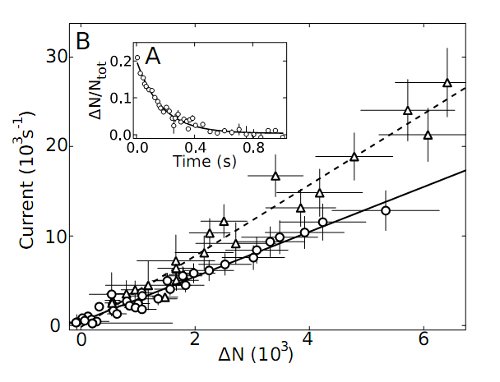
A (Inset): The exponentially decaying "current." B: The current as a function of the number imbalance.
The inset graph (part A of the figure) shows the exponentially decreasing number imbalance, which is mathematically identical to the voltage across a capacitor. From those decay graphs, they can extract a "current," namely the rate of flow of atoms from one side to the other. The main graph plots that current as a function of the number imbalance, producing a nice straight line.
So.... Current is proportional to voltage? You mean, they did all this to rediscover Ohm's Law? Yes and no. It is very much an ohmic behavior, because if you look closely, you see two sets of points giving two different straight lines. Those correspond to two different widths of the channel between the sides. And just as you expect, the "current" is higher for a wider channel than a narrower one.
There is something sort of surprising about this, though, when you think about it on a microscopic level.
Which is what? Well, when they do this, they tune the interactions between the atoms so that they basically never collide. The "mean free path" of the atoms, which is the average distance an atom travels before hitting another atom, is more than 20 times longer than the length of the channel. There's nothing physically blocking the atoms from flying right through the channel-- in fact, an atom that enters the channel will always exit the other side without slowing down along the way. This is termed "ballistic," a term that will always have a special place in my heart thanks to an incident at my Ph.D. defense.
Which was what? Let's just leave that hanging to see if anybody actually reads this far. I can explain it in a comment if people want to know.
OK, so if there's nothing physically blocking the atoms, what causes the resistance? That's the cool thing. It's basically a Pauli exclusion thing-- there are only so many ways that an atom can pass through the channel, and each atom that occupies one of these blocks any other atom from simultaneously taking the same path. So, while there's no physical blockage due to collisions between atoms, there's a blockage caused by physics-- the quantum rules governing fermions limit the capacity of the channel, and give you ohmic behavior.
Yeah, but how can you be sure that's what's going on? I mean, maybe there's just some bumps in their microscopic channel that gum everything up. True, that could be a problem. But that's the really cool part of this, and the thing that really shows the advantages of the ultracold-atom system: they can measure this directly, by zooming in on the channel region.
They do what, now? They have a very high magnification imaging system that lets them take pictures of an area about the width of a human hair right at the position of the channel. The model where resistance comes from a Pauli-type blockage says that the density of atoms inside the channel should be pretty much constant-- not many can get in there, but once they do get in, they fly straight across without slowing or stopping. And that's just what they see from the red points on this graph:
If you follow the red points as you move across the channel from left to right, you see an initial low density (the side that's short on atoms) that initially increases (a pile-up of atoms at the entrance to the channel), then goes flat across the channel itself (the expected constant density in the channel), then increases again (pileup at the other side), and reaches a high density on the side with extra atoms. That's exactly what you expect for the ballistic case.
Yeah, but that doesn't show that their channel isn't messed up. Right, which is why there are also blue points on that graph. The blue points are a case where they deliberately screw up the quality of the channel by adding some random intensity variations. These physically slow down the atoms as they cross, putting it into a "diffusive" situation. In that case, you expect the density to drop smoothly from one side to the other, and that's just what you see. There isn't the clear plateau in the channel region that you see in the red points.
OK, I admit, that's pretty clever. Yep. Which is why it's in Science.
This is also very much a proof-of-principle type experiment. They're showing the simplest things they can do with this system, but there are lots of fun extensions, many of them using their high-magnification imaging system to manipulate the channel region. They can also make analogues of a specific type of transistor, by adding an extra laser beam, and look at the microscopic behavior of those.
So, is this going to help computer engineering keep up with Moore's Law, making even smaller transistors? Well, no. But it does give a nice way to probe the basic physics of these systems in an extremely well-controlled way, allowing detailed tests of the theory.
And, more importantly, it's just really, really cool.
Like, 250 nanokelvin cool? OK, that's awful. I think we're done, here.
Brantut JP, Meineke J, Stadler D, Krinner S, & Esslinger T (2012). Conduction of ultracold fermions through a mesoscopic channel. Science (New York, N.Y.), 337 (6098), 1069-71 PMID: 22859818
- Log in to post comments




Let’s just leave that hanging to see if anybody actually reads this far.
OK, I'll bite. That sounds like it might have been a True Lab Story.
Tell us about "ballistic" please!
I'm having trouble visualizing the shadow in the laser and the resulting "wire". The laser is shining in line with the resulting division between the atoms, right? So, assuming a round cross section for the laser, in order to block part of the laser and make the connection between two sides, you have to block out a diameter of the beam. But that's going to create a flat "wire" which runs the entire depth of the collection of atoms, instead of a cylinder, right?
Do they use a second beam at a right angle to clear out most of the depth? Or is that not important? I assume the wire can't be deep, because that would allow more states and you'd get more than one atom passing across it at a time.
My understanding was that they have only one laser in there, and it does go the full width of the cloud. The cloud is a long ellipsoid, with the depth into the picture above being roughly the same as the vertical height, not the horizontal width, so it's not that wide a wire. they describe it as "quasi-two-dimensional" at one point, which would be consistent with that.
There are, in fact, multiple atoms crossing the channel at any given time, due to the relatively large width of the "wire." One of the possible extensions they suggest is to introduce another beam through the high-magnification imaging system (which is perpendicular to the imaging used for the picture at the top of this post, basically looking down from above) that would reduce the width of the channel to a point where only a few, maybe even one, atom could cross at a time. Then you'd see some quantization of the current, which would be pretty cool.
@Tom Singer: See Figure 1 of the paper (http://arxiv.org/abs/1203.1927, linked at the top of the post). The channel is effectively two dimensional, making use of the null waist of a two-lobe (TEM_01) beam, to create a gap which is narrow in Z, but broad in X and Y.
@Chad Orzel: You got to Tom's query before I did. So what about your "ballistic" defense experience? Are you just waiting for enough votes to come in, or should we start trying to guess? I'm hoping its something Mythbusters-related (http://www.youtube.com/watch?v=BJY45bADSqQ)...
I'll write up the "ballistic" story as a top-level post tonight after the kids are in bed. I have a bunch of work I need to do before day care ends, though.
Here's another ballistic atom paper (only in preprint form at the moment), "Observation of Free-Space Single-Atom Matterwave Interference," http://arxiv.org/abs/1208.4868v1.
The authors use an optical-tweezer system to launch and interrogate individual cesium atoms, one at a time, through a gravitational interferometer system (see, for example, http://arxiv.org/abs/0809.1054).
They have a really nice plot in the paper (Fig. 2) showing how the interference fringe become visible with increasing statistics, where each entry in the plot comes from a single atom's self-interference.
Thanks, Chad and Michael.
Does the resistance/number of possible states vary linearly with the cross section of the channel in a similar way as an electrical conductor would? I guess with a sufficiently small number of states, you'd see stepping behavior, similar to the quantization of the current.