Using Light to Put a Mirror in the Dark: "Optomechanical Dark Mode"

In which I unpack a cryptic paper title and explain how quantum superposition lets you use light to keep things from interacting with light.

-------------

I joined AAAS a couple of years ago to get a break on the registration fee for their meeting, and I've kept up the membership mostly because I like having individual access to Science articles, so I can read them in the coffee shops where I get actual work done. This also gives me access to articles in the "advance online publication" stage, which is hilarious because Union's institutional subscription doesn't include those articles-- if I'm reading on the campus network, I need to log out of the college's subscription and log back in as myself to read them.

Anyway, a recent online advance publication that caught my eye was this: Optomechanical Dark Mode. I can't do a full ResearchBlogging treatment of this, because I can't find a readily accessible version of it (yet-- sometimes these show up on the arxiv after they appear in the print edition), but it did suggest a physics-explainer post, so we'll take a whack at the underlying science, in the traditional Q&A format:

OK, what's all this about, then? None of those words make sense. This is a somewhat cryptic sounding title, but "optomechanical" means they're talking about a system where they worry about the coupling between light and some movable optical element, usually a mirror. These kind of systems have generated a lot of interest recently, because with a clever arrangement of the system, the light bouncing off a movable mirror can be used to "cool" the mirror's motion, getting it toward the quantum-mechanical ground state for the system. This is one way you might think about seeing quantum mechanical superposition states of relatively large objects-- things a micron or so across, containing huge numbers of atoms.

So, what's a "dark mode"? Well, "mode" is a kind of flexible term in quantum optics, but it basically specifies a particular state of a quantum optical system: a photon with a particular wavelength propagating in a particular direction, say, or in this case, a particular motion of the mirror.

What do you mean? Like, moving to the left, vs. moving to the right? No, it's more complicated than that. It might seem like when you're talking about the motion of some object, you just want to give its instantaneous position and velocity, but it turns out that it's mathematically useful to describe it instead as a collection of oscillating modes-- moving back and forth at a whole range of different frequencies. If you treat the mirror as a thing that is oscillating back and forth by some amount at one frequency, and by a different amount at twice that frequency, and by yet another amount at three times that frequency, etc., you can exactly predict the position and velocity, but in a way that's easier to work with.

So, this is just a mathematical trick? Not exactly-- there's a sense in which the oscillating-mode description is more fundamental. Particularly when you're talking about quantum mechanical systems, in which the amplitude (how far it's moving back and forth at a given frequency) can only take on discrete values. For quantum systems, the object can only be found moving back and forth at particular allowed frequencies, by integer multiples of some fundamental distance associated with that mode.

That sounds weird, but OK. So, an optomechanical mode is some combination of light doing one thing, and the mirror moving back and forth at some frequency? Exactly.

So, what does "dark" mean? It means that this particular mode doesn't couple to the light.

Wait, what? It means that the mode they're talking about doesn't affect the light field, and vice versa. It's a "dark mode" because when the system is in that mode, it doesn't absorb energy from the light, or lose energy from the motion into the light field.

That doesn't make any sense at all. Yes, it does. It's just kind of a subtle point, and easier to explain when you're talking about atoms than a moving mirror. Let's look at the figure that's the "featured image" for this post, which I will reproduce below for the benefit of people reading via RSS:

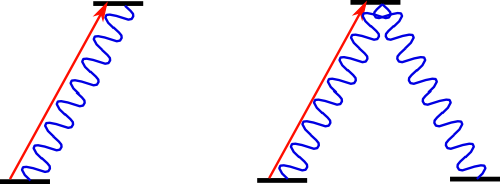
A laser (red arrow) exciting an atom. On the left, an atom with only two levels must return to the same initial state; on the right, the atom can decay into a superposition of two states.

This is an abstract representation of an atom interacting with light to produce a dark state. On the left, we have the simplest toy model you can imagine, an atom with only two energy states, represented by the horizontal lines. This atom starts out in the lowest energy state (the "ground state"), and interacts with a laser tuned to exactly the right frequency, represented by the red arrow, which moves the atom from the lowest energy state to the upper (excited) state.

And once it's there, it can return to the ground state by emitting a photon, which is the squiggly blue line, right? Exactly. The different color, by the way, is just to emphasize that it's a different mechanism-- both photons have the same color. For a two-level system, the atom can absorb a photon and go up, and it can emit a photon and come back down, and that's it.

So where's the dark stuff? Dark state. To get a dark state, you need a more complicated system, but as a famous misquote of Bill Phillips says, "there are no two-level atoms, and sodium is not one of them." Real atoms have lots of energy states, and the right side of the figure shows another possible arrangement, with two low-energy states having almost exactly the same energy.

That can happen? Sure, there are lots of states in real atoms that have the same or almost the same energy. They're called "degenerate states" for some reason.

Is this the place where you make a joke about Erwin Schrödinger shacking up with two different women at the same time? If you like, sure, but I think you already covered that.

Right, then, moving along. What do these degenerate states do? Well, in the three-level system, the atom in the excited state has options. When it decays, it can go back to the same state it started in, or--

Or it can go into the other state. Right. So there are two options. Actualy, there are more options than that. It can decay to either of the two lower states, or into a superposition of both at the same time. And there are all sorts of superpositions possible.

So... It emits two photons at once? No, just one, but it ends up spread between the two ground states, rather than definitely in one or the other. The two states have nearly the same energy, so that's not a problem, and while they would generally require different polarizations of light, that's not a problem either (one right-hand-circular, the other left-hand-circular, say), because a photon in a superposition of two polarization states is just a photon with some other definite polarization (an equal superposition of both circular polarizations, for example, is just a linear polarization at some angle).

You can also do this sort of thing with lower-energy states having two different energies, though that generally involves "Raman transitions," with more than one laser frequency, and stimulated as well as spontaneous emission. The end result is the same, though: an atom that's in a superposition of two states at once. Which, if you do it right, produces a dark state that won't absorb light from the laser.

Because the part of the atom that's in the other state from the one it started in can't absorb the light? In a very simple sense, that could count as a dark state, sure, but we're talking about states with the same energy, so the same laser field could excite atoms from either low-energy state. There's a particular combination of the two, though, that won't absorb light even though either of the two individually would happily absorb laser light.

How can that be possible? Well, you need to remember that we're dealing with quantum systems here, and everything is in some sense a wave. So when you look at trying to excite the atom from the superposition state up to the excited state, what you really have is a bit of a wave coming from the low-energy state on the left trying to get into the excited state, added to a bit of a wave coming from the low-energy state on the right trying to get into the same excited state.

Ohhhh.... I see. When you add the two waves together, they can cancel each other out! Exactly. If the peaks of one wave fall into the valleys of the other, they add together to give you nothing at all. Since these are waves describing the probability of finding the atom in a particular state, "nothing at all" means "no probability of the atom ending up in the excited state," which means that it doesn't absorb the light at all. Thus, a dark state.

That's pretty cool. It must be hard to arrange these states, though. Not really. You're almost guaranteed to have some superposition of the low-energy states that is dark, and once you have that, you automatically end up with atoms in that state.

How do you figure? Well, when the excited atoms decay, they can go into any possible combination of the low-energy states. If they end up in one that can absorb laser light, they'll get excited again, and decay again. Once they happen to decay into the dark state, though, they stay there.

Because the atoms by definition don't absorb light in that state? Exactly. This is a col quantum trick that AMO physicists exploit for a lot of neat experiments that have daunting names like "Velocity Selective Coherent Population Trapping" or "Electromagnetically Induced Transparency." The core idea of all of those things, though, is that if you arrange things properly, you can put atoms in a state where they cannot possibly absorb light from the laser, and once you set up such a system, those atoms that can absorb light will eventually be driven into the dark state.

So, what these people did with this mirror is like that, but with a mirror rather than an atom? Exactly. It's a much more complicated system-- they need two different laser frequencies, and it only works for a particular frequency of the mirror moving back and forth-- but for the right arrangement of their system, they get a state where the mirror moving at a particular frequency isn't disturbed by the light, and the light isn't disturbed by thermal excitation of the mirror.

And this matters... why? Well, a lot of the things you might use an optomechanical system for can be screwed up by fluctuations in the state of one or the other. If you're doing something like LIGO, for example, you want to make sure that small changes in the intensity of your laser aren't making the mirrors shake in a way that would look like a gravity wave passing by. Or if you're using one of these systems to look at quantum information stored in the light, you don't want the random jiggling of the mirror because it's not cooled to absolute zero to affect the photons hitting the mirror. Being able to put the system in a dark mode is a possible way to get around both of those problems.

So, there are potential implications for future work using optomechanical technology, which is why this got into Science. But mostly, this is just kind of awesome, exploiting quantum superpositions to do something counter-intuitive: using interactions with light to make sure that some object can't interact with the light.

Yeah, I guess that is pretty neat. Thanks. No problem. I wish I had time to do more of these...