My Claim to Scientific Fame: "Squeezed States in a Bose-Einstein Condensate"

In Monday's post on squeezed states, I mentioned that I really liked the question because I had done work on the subject. This is, in fact, my claim to scientific fame (well, before the talking-to-the-dog thing, anyway)-- I'm the first author on a Science paper with more than 500 citations having to do with squeezed states. And since I've never written it up on the blog before, I'll leap on this opportunity to do some shameless self-promotion...

Well, aren't we Mr. Ego today? What's this paper that you're so impressed with about? I've never been all that good with titles, but I like to think this one was kind of self-explanatory: we took a Bose-Einstein Condensate (a more serious description here), and made squeezed states in it.

So, like, you shone a laser into it, and reduced the uncertainty in the phase of the laser beam? No, this wasn't a squeezed state of light, but a squeezed state of atoms. This was a fairly early experiment in what you might call "quantum atom optics," where the atoms of the BEC behaved in the same way as photons in a squeezed state of light.

What got squeezed, though? Did you distort the atoms, or something? No, we manipulated the statistical distribution of the atoms after we chopped a single condensate up into about a dozen smaller pieces using an optical lattice. By controlling the properties of the condensate and the lattice, we could reduce the uncertainty in the number of atoms in one of the pieces from something like plus or minus 50 atoms to around plus or minus 2.

Wait, there's uncertainty in the number of atoms? What, are you creating and destroying matter, here? The total number of atoms in the condensate as a whole is fixed, but when you chop it into pieces, you get an uncertainty in the number of atoms in each piece. Since all the atoms in the condensate are occupying the same wavefunction, the division is a quantum process, and leads to uncertainty in the number of atoms in each piece. That uncertainty is the thing we manipulated.

OK, how did you do that? By just counting the pieces very carefully? No, our imaging system was nowhere near good enough for that. What we did was to exploit the interactions between the atoms to stop atoms from moving between pieces.

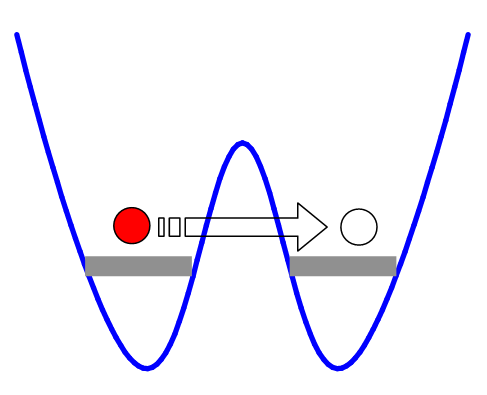
This is easiest to understand by making one of those spherical-cow approximations physicists are fond of, thinking about a double-well system, where you have a single condensate that you split into two pieces by raising an energy barrier between the two. Classical particles with low energy would be absolutely forbidden from passing between the two states, but quantum mechanics allows "tunneling," in which quantum particles can pass through energy barriers even if they would classically be blocked. Schematically, it looks sort of like this:

An atom tunneling between sites of a double well system.

This process is exactly what you need in order to have uncertainty in the number of atoms in each well. On average, you expect them to be equally split, but tunneling lets you move atoms from one side to the other, giving you the ability to have unequal numbers. If you work out the math, the probability of finding a given number of atoms on either side of the barrier follows a Poisson distribution, and the uncertainty is equal to the square root of the average number of atoms (that is, the square root of half the total number in both wells).

So, you made a squeezed state by shutting this tunneling off? By what, just making the barrier really high? Making the barrier higher would reduce the rate of tunneling, but all that would really do is to slow the process down. Atoms could still move back and forth, just very slowly, so the many-body ground state would still be a Poisson distribution. A higher barrier by itself would just make it take longer to prepare the system in that many-body ground state (which we did by verrrry sloooowly raising the barrier height, so that the process remained adiabatic). To get squeezing, we needed to exploit another factor, namely the interaction between atoms.

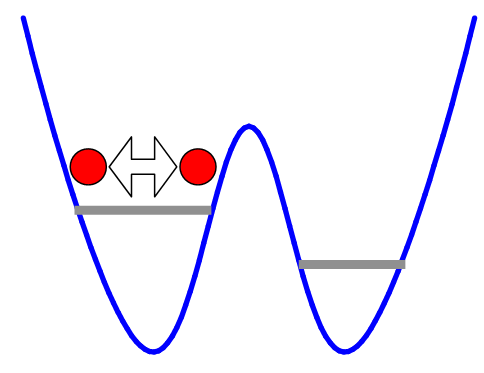
OK, what? Well, the atoms we used were real atoms, not the ideal perfectly non-interacting atoms of theory. That means that they could collide with each other, and those collisions would increase the energy of all the atoms in a given well every time you added a new one. Schematically, it looks like this:

Atoms colliding with each other shift the energy levels in a double well.

The key here is that this shifts the energy of every atom in the well (because they're bosons, and all occupy a single quantum state). Which means that, when you have more atoms on one side of the barrier than on the other, the energies of the lowest-energy states on the two sides no longer overlap.

That, it turns out, is enough to shut off the tunneling in a way that changes the character of the many-body ground state of the system. In order for atoms to tunnel from one site to another, there needs to be a state in the new well for them to land in. When you have interactions between the atoms, that shifts the position of the energy states in the new well-- the side gaining an atom sees the energy of all of them increase, and the side losing an atom sees the energy of all the remaining atoms decrease. Eventually you hit a point where adding one more atom would move the states far enough apart that the tunneling can't happen. That puts a cap (of sorts) on the number of atoms you can shift from one site to another, which in turn limits the uncertainty in the number of atoms in a single well.

Now, in practice, there's a trade-off between two factors: the atom-atom interaction, which in the notation we used was characterized by a bundle of symbols: Ngβ; and the tunneling rate, which gets the symbol γ. The ratio of those two is the key parameter, but the experimental knob we used to control that ratio was the height of the energy barrier between the wells, which is simply related to the intensity of a laser that we could control very well.

So, what you're saying is that you did turn off the tunneling by making the barrier really big... Well, yes, but not for the reason you were suggesting earlier. Or, to put it another way, the meaning of "really big" was set by the interaction between atoms, not the tunneling rate itself.

That's a little weaselly, but we'll write it off as being married to a lawyer, and move on. So, once you turned off the tunneling, how did you see the change in the uncertainty? You already said you didn't have the resolution to count atoms. We exploited the Uncertainty Principle. Remember, the definition of a squeezed state is that you decrease the uncertainty in one quantity at the price of increasing it in a different quantity. In this case, we decreased the uncertainty in the number of atoms in each piece of the chopped-up condensate at the cost of increasing the uncertainty in the phase of the wavefunction associated with each piece.

But how do you measure the phase? I thought that was a property whose absolute value you couldn't determine? You can't determine the phase of a single wavefunction in any meaningful sense, but you can determine the phase difference between two different wavefunctions by interfering them with each other. And in this case, we had a dozen different wavefunctions, corresponding to the dozen different pieces of our chopped-up condensate, each with a random phase distributed over some uncertainty range.

When we shut off the lattice, each of the different pieces acted like a source of waves that spread out and interfered. When the phase uncertainty was small, we'd see a nice, clear interference pattern with two sharp peaks. As the phase uncertainty increased (because we increased the height of the barrier between pieces of the condensate), the contrast in that interference pattern went down. Like this:

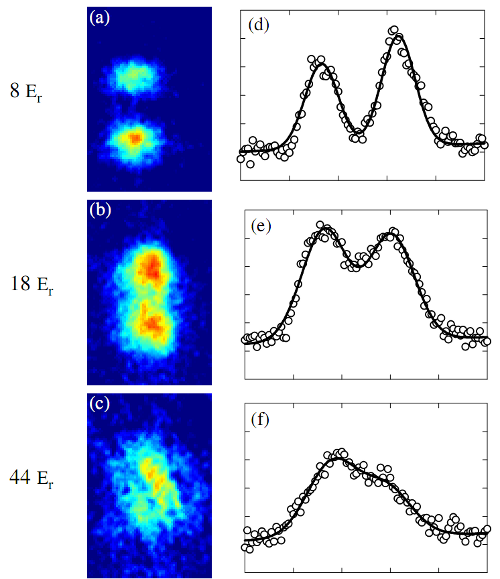An alternate version of Figure 1 from the paper, showing the loss of interference as the lattice depth is increased.

At the top, we have a lattice with low barriers, and low phase uncertainty. As we increase the energy barrier (the exact values are on the left), the contrast goes away, showing the increase in the phase uncertainty. By comparing a whole slew of images like these to MATLAB simulations of the interference pattern, we could work out what the phase uncertainty was, and thus how much squeezing we did. Our best guess at that was that we squeezed the atom number by around a factor of 25; since on average we had about 2500 atoms per piece, that corresponds to a decrease from the Poissonian uncertainty of 50 (square root of 2500) to an uncertainty of around 2 atoms per site.

And yet, you never actually measured the number of atoms per site? Nope. Pretty clever, huh?

It's very cute. But... How can you be sure you weren't just screwing up the contrast in some other way? I mean, you usually have to work pretty hard to see atoms interfering, don't you? Absolutely. And a big chunk of the paper is devoted to finding ways to show that what we saw was really a many-body quantum mechanical effect, and not just a technical error.

One possibility we looked at was that we were just seeing a slow evolution of the phases due to the long time we spent ramping up the lattice. We typically used a 200 ms ramp up, which is an eternity in atomic physics, and you might suspect that some garbage effect caused the phases of the individual pieces to drift apart during that time. We could rule that out, though, by watching the traps evolve for a long time: we held the pieces in the lattice at different depths for hundreds of milliseconds, and didn't see any significant change in the contrast. We also deliberately screwed it up, by slamming the lattice up to its full value really quickly, which should just separate the pieces in a way that causes their phase to evolve independently. As expected, we saw the contrast start out good, and over a few tens of millisecond, it would disappear as the pieces drifted apart in phase.

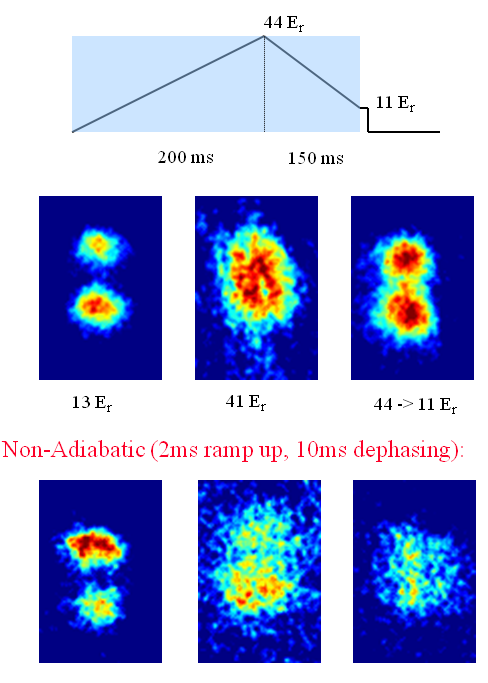
My favorite of the tests, though, is the one that I used as the "featured image" at the top of this post, which I will reproduce here:

A version of Figure 4 from the paper discussed in the post, taken from an old talk.

This shows the results of two different experiments. The top row of pictures is represented schematically by the line diagram at the top: we ramped the lattice up slowly to some maximum value where we would have a squeezed state, then ramped it back down equally slowly to a level where we expected good contrast. If, as we claimed, we were changing the nature of the ground state from a coherent state to a squeezed state, this process ought to bring it back to a coherent state, and that's exactly what we saw. The left picture is the good-contrast image from ramping directly to the lower lattice level, the middle picture is the bad-contrast image from ramping up to the squeezed state level, and the right picture is what we got after ramping up and back down. It's not perfectly identical to the left image, but it's pretty damn good.

But couldn't that slow ramp down just be giving you enough time to re-establish a good phase after you screwed it up some other way? That's what the bottom row of pictures is for. In that case, we slammed the lattice on quickly, held it for long enough to get a bad-contrast image from the random dephasing, then did the same slow ramp down. Which utterly fails to show a return of the contrast, providing really good evidence that we were, in fact, making squeezed states like we said we were.

So, what's the end result of all this? Well, we demonstrated the ability to directly manipulate the number statistics and uncertainty of an atomic system, exploiting the Uncertainty Principle to both make the squeezed state and observe it. Also, this was my post-doctoral research, so in a very real way, this paper got me my current job. Which might not be a big deal for physics as a whole, but I think it's pretty awesome.

I guess that is cool. So, since you're the author of this paper, would you care to share any salacious details of its writing? "Salacious?" Um, no. I do have some vaguely amusing anecdotes about the research and writing process, though. But this post is already pretty long, so we'll save that for another day.

You're just looking for another day worth of bloggy ego-boost, aren't you? I can neither confirm nor deny that extremely plausible explanation.

(NOTE: The images in this post are all taken from the slides for my job talk about this stuff. The paper is paywalled, and old enough that I wasn't putting things on the arxiv yet, so I can't point you to a free version, alas... If you really want to read it, though, email me and I can send you a copy.)

Orzel, C., Tuchman, A. K., Fenselau, M. L., Yasuda, M., & Kasevich, M. A. (2001). Squeezed States in a Bose-Einstein Condensate Science, 291 (5512), 2386-2390 DOI: 10.1126/science.1058149