We spent this past weekend in Florida, visiting Kate's mom and her husband, who moved down there in October. This was a huge hit with the kids, who were very excited to fly on an airplane (four of them, actually, as we changed planes in Baltimore both ways). They also got a big kick out of driving around in a rental car-- The Pip chattered happily about "My new car" for a while-- which we did a lot of, going to a beach and the Mote Aquarium in Sarasota.
Doing all that driving in a rented SUV and a state with a 70mph speed limit got me thinking about optimum driving speed. Particularly on the trip back to the airport, where I was trying to eke out the last few miles on the single tank of gas I had purchased from Hertz (I managed to roll in with the needle just hitting E, and the rental return person complimented me on getting the most out of that tank).
It's well known, of course, that the efficiency of a car engine drops as the speed increases-- the force of air resistance increases as you go up in speed, probably as something like the square of the speed, so the engine needs to work harder to maintain the same speed, and burns more gas. You can find any number of sites that sanctimoniously lecture you about how much better your car would run if you would just drive at 55mph everywhere-- this one even includes a price calculator.
Of course, there's something fundamentally disingenuous about these calculations, namely that they assume the time you spend driving is free. I could, that calculator informs me, save $467 a year by driving at 60mph instead of 75mph for a 30-mile commute, at the cost of only 6 minutes per day. Which sounds like a great deal, provided I don't put any value on my time.
But, of course, time behind the wheel is time not doing anything else, and if we're going to properly calculate an optimum speed, we really ought to put some monetary value on that, as well. As this classic xkcd reminds us.
If we attach a monetary value to the time spent driving, then the optimum speed is not necessarily the speed at which the engine is most efficient. The cost of fuel will be lowest at the maximum efficiency point, of course, but that's only a part of the equation. You also need to figure in the cost of your time. So, fuel costs will go up as the speed increases, because the engine works less well, but personal time costs will go down, because the higher speed reduces the time in transit, and thus the number of hours you're "paying" yourself for. At some point, those two trends will cross over, and there will be an optimum speed where the total cost is a minimum.
How does this work out in practice? I originally planned to do this as a post with equations, setting up some toy model for the efficiency, adding the increasing time cost, and doing freshman calculus to find the optimum speed where the cost was minimized. When I went looking for numbers, though, the figures for the efficiency look like a more complicated function than I want to try to figure out, so we'll do this by an empirical method.
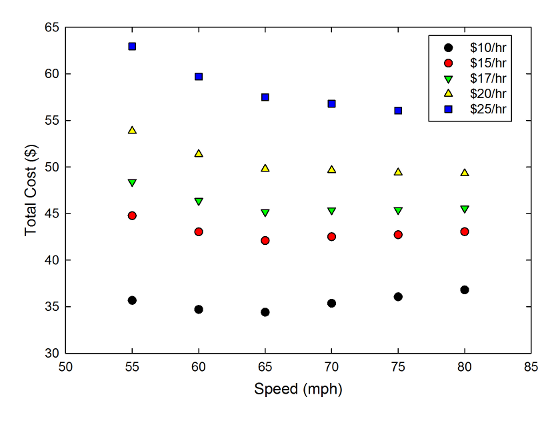
That fuel cost calculator page gives approximate values of the decrease in efficiency for speeds above 55mph, so we'll use those six points, and calculate the total cost for a 100 mile trip, assuming different hourly rates and gas at $3.50/gallon. If we do that for a rental SUV getting 20mpg (which is probably not a horrible guess for the car we were driving this past weekend), we get the following graph:
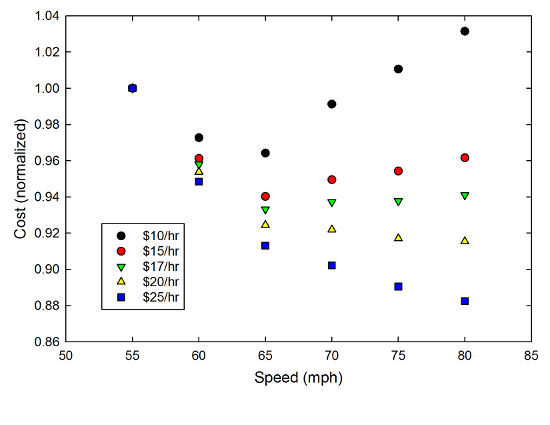
As your hourly rate increases from $10/hr to $25/hr, the total cost of the trip increases, because they all take some time, and you pay for that time. If you look closely, though, you can see a trend in the points for each color, particularly at the lower pay rates-- at lower speed, the cost is a little higher because of the increased time. At lower pay rates, there's a minimum value of the total cost, at around 65mph, because the fuel cost eventually overcomes the increased time. You can see this trend slightly better if we normalize all the points to their value at the maximum efficiency point of 55mph:
Here you see that, as a fraction of the initial cost, the total cost drops as you increase the speed, up to a point, then at the low pay rates, goes back up. For higher pay rates, though, the cost of the fuel just isn't that significant compared to the cost of the time, so the curve flattens out, and then for the highest pay rates, continues to drop. So, according to this calculation, if you value your personal time at $20/hr or more, you should drive at 80mph. If your personal time is worth $17/hr or less, the optimum speed is around 65mph.
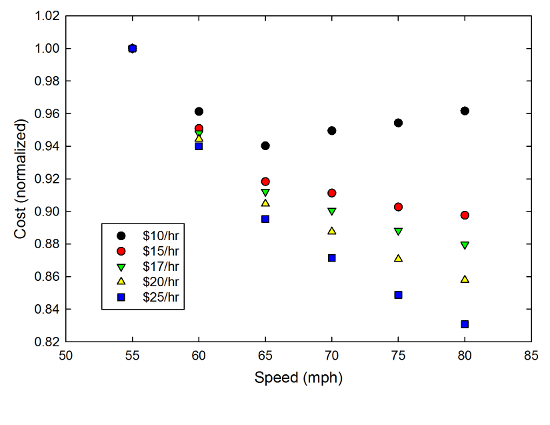
Of course, this also depends on the efficiency of your car. If instead of an SUV we were driving a higher-efficiency vehicle with some sort of internal pocket dimension to hold all the crap that's required when you travel with kids, the normalized cost graph for a 30mpg car looks like this:
So, if your car gets 30mpg at 55mph, and you vale your time at $15/hr or above, you should drive as fast as you can. Time is money, and it's more money than the gas you burn.
Of course, if I stop there, this not-entirely-serious post is all but guaranteed to get me some comments from tiresome scolds telling me I'm a horrible person for not regarding energy efficiency as the be-all and end-all of everything. And it's true, I'm a terrible person. I also shower with the lights on, thus wasting electricity.
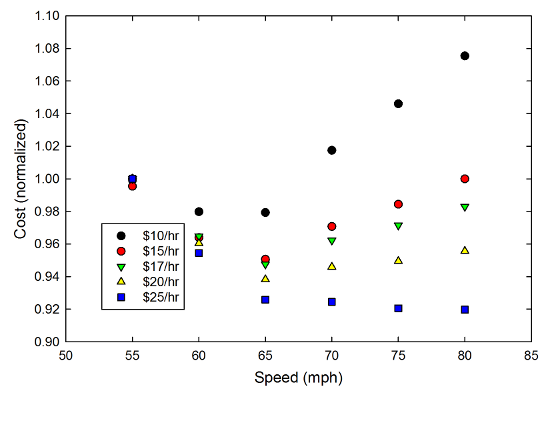
Of course, those issues are, in principle, something we could capture in this model by increasing the effective price of gas to more appropriately capture the externalities of carbon emissions and pollution, etc. If we bump the price of gas in the toy model up from $3.50/gallon to $4.50/gallon, the result looks like this:
That's got a minimum cost point at lower speed for all but the highest pay rate. And if you bumped the cost of gas up even more, even the high-salary folks would no doubt stop benefiting from driving at maximum speed. Then it's all a question of arguing about what the "right" price of gas is, and what the "right" value to put on your time is. Should you be billing your free time at the same rate as your salary? More? Less? And how do we price in the likelihood of getting a speeding ticket at the high end of these graphs?
Those are all interesting questions, but I've already devoted more time to getting this out of my head than I ought to, and need to get back to writing my book. Time is word count, and word count is money, too.
- Log in to post comments

It's interesting that the inflection points, when they happen, all seem to happen at about 65mph or so.
I wonder if that's some generalized feature, or a result of some other variable in the system that was held constant. The trip length, perhaps? Would that inflection point change if it was a 20 mile outing rather than a 100 mile weekend? Or a 6000 mile cross-country road trip?
That's an artifact of the small range of parameters used, I think. I did a couple other runs with vastly different values for the gas price-- up to $15/gallon, and you get more of a spread in the location of the inflection point with that. It's also very coarse-grained with just six speed points, so it's hard to see small differences.
The trip length shouldn't change much, as it's a common multiplicative factor in both components of the cost. I think it just factors out.
The biggest cost of inefficient driving habits is added CO2 in the atmosphere, the effects of which we read about daily. The cost of climate change will hit your kids regardless of your hourly rate of pay.
What to do about this:
Get a "ScanGauge" (online price about $180, also available at some auto parts stores). This is a real-time and cumulative MPG meter that plugs into the data port on any car 1996 or later (usually under and to the side of the steering wheel). When people see their realtime MPG, they typically adjust their driving to improve efficiency.
My vehicle is rated at 22 city, 25 highway. Using ScanGauge and driving aware, I typically get 35 on the highway, 32 on combined trips that are mostly highway with some city, and 24 city as long as it's not stop-and-go.
Something else I did, was set the "price per gallon of gas" function to $1.00, which turns the "trip cost" function into a "gallons used for this trip" function. This lets me compare different routes to a destination: such as a shorter route with worse traffic, and a longer route with less traffic, to find the route that uses the least actual gasoline regardless of MPG.
I don't know if there's time to get these shipped in time for Christmas, but you can always give "New Year's presents." Tell people, "this will help you save money including wear & tear on your engine & drivetrain."
Lastly, slowing down = safer driving, and no more "exceeding the posted limit" tickets. The latter item by itself will pay for the ScanGauge unit.
No, I don't work for them. Just a highly satisfied user.
I think you are overthinking this.
If you are in a hurry to get where you are going, drive fast. If not - relax.
I shower with the lights off. But only because it's relaxing.
It would be useful (FWIW) to see this expanded with $50/hr and $75/hr or higher (effective billing rates for a variety of consultants, lawyers, etc). Thanks.
What a very US centric post. My family sized diesel car gets 65mpg average in all driving, including at the uk limit of 70mph. The MPV I had previously did 50 mpg. Diesel costs $9.80 per gallon (petrol is slightly cheaper). These figures are linked, more expensive fuel may not slow you down, but it does encourage you to buy a more efficient car.
You also have to factor in road conditions (the objective is to get wherever you are going, preferably in one piece) and the likelihood of being pulled over by the state police/highway patrol/RCMP/whatever (I don't have hard numbers, but I suspect this is a monotonically increasing function of the difference between your speed and the posted limit, and in most states the fines if you get a ticket are a monotonically increasing function of that difference). The former is a serious consideration where I live; on single carriageway roads your speed is effectively limited to that of the car in front of you. The latter is a small consideration, or at least is treated as such in this area. But the last couple of times I drove to Montreal, I saw billboards along the autoroutes reminding drivers that (loosely translated from the French) the freeway is not a race track, and that hefty fines and license points await drivers caught driving 160 km/h. So at least some government officials in North America think this is a problem that needs to be dealt with.
Given an optimum motor oil (e.g. Mobil 1), anti-pollution spaghetti, a low Cd shape, and a 5-speed transmission, then your optimum mileage is achieved by 1) continuous motoring. Traffic lights are carefully anti-synchronous to maximize pollution (more regulation) and minimize gas mileage (more sales tax); 2) toodling along where the pollution hardware cuts back and the engine+transmission reach maximum efficiency. That is often mid-70s mph.
A 2012 Honda Civic averaging about 75 mph for the trip (ho ho) with widows closed and air conditioner running, from Orange County, CA to Tuscon, AZ and back along I-10, averaged a bit over 39 mpg (5W20 Mobil 1, drank no oil). In the city, 30 mpg is SOP. Try going anywhere on Orange County surface streets that is averages faster than a well-pumped bicycle.
It's way cheaper for you to fill the tank (away form major hubs, certainly with off-brand gasoline) than for Hertz to charge you for the fill.
As noted in #3 increased speed means an increased likelihood of having an accident. Calculations of the optimum speed have been carried out for the UK, taking into account all costs and taking an average value of time. The outcome was that the optimum speed on motorways (freeways) was found to be about 70 mph and on urban roads about 30 mpg. This varies according to the accident risks for roads of different natures.
Re. #7: That's the legitimate rationale for corporate jets: you have a high-cost / high-value person who has to get from A to B in the minimal time, to perform some critical function that can't be done via telecoms. So, put them on the Lear Jet and have a limousine meet them at the airport.
The ferocious inefficiency of those means of transport are offset by the value of the work the person performs, and the hypothetical benefit of that work to various stakeholders.
However, any corporation that has committed to sustainable policies, will seek to reduce the use of corporate jets and suchlike to the absolute minimum. In many cases that will turn out to be zero if headquarters and other properties are in locations that are well-served by other modes of transport, and if serious efforts are made to use telecoms for all they're worth.
For example, anyone who works in an office, whose job consists of using a telephone and computer all day, can do that job from a home office over a VPN. Telecommuting and telework should be given major tax incentives, and then we will see them happen on a scale that takes more cars off the road than anything.
For example, anyone who works in an office, whose job consists of using a telephone and computer all day, can do that job from a home office over a VPN.
There are various reasons, some good and some not, that this scheme has not been implemented in many workplaces. One of the good reasons is that East African plains apes have a well-documented need for social interaction, and some of this social interaction takes the form of what we call meetings. Technology can reduce the frequency of many such interactions, but it hasn't eliminated the need.
Oh my, that was fast!;-)
I'll take it that by "East African plains apes" you mean Homo Sapiens generally. True enough, but no doubt you know that the youngsters today don't have telephone conversations any more: they all have cellphones with 1934 audio quality, so they send little telegrams back and forth, called "texts," even when they're sitting together at restaurants.
As for "meetings," I understand your point in a strictly clinical way (hmm, so that's what humans do...), but the degree to which people "at work" spend time doing anything-but-work continues to amaze.
Anyway, bottom line is, humans will find ways to socialize even if deprived of "meetings." They'll push a button on their home VOIP extension from the office PBX, to transfer calls to their cellphones (I invented that feature), and go hang out with their neighbors on the porch. They'll have "kid co-ops" to keep track of each others' kids, and interact with their neighbors that way. They'll have their personal screen-device plugged in next to their office screen-device so they can chatter and send little telegrams to friends all day, and hang out online whilst they're "at work."
But work will get done, and socializing won't suffer, and CO2 emissions will come down. Or none of the above, and here comes +5 Celsius in our kids' lifetimes.
State Troopers must be be highly paid!
I'm completely irrational about business travel costs. The company pays for my air and car transportation and pays me by the hour. So I should travel as slowly as possible in all cases to maximize my pay. But I still choose nonstop over longer connecting flights, and drive at the prevailing highway speed instead of the minimum allowable speed. This behavior probably costs me thousands of dollars a year.