Trains of Clocks

My Gen Ed relativity course has mostly been me lecturing about stuff to this point, so on Wednesday I decided to shake things up a bit and convert a chapter of David Mermin's It's About Time. The idea was to get students up and moving around a bit, and actually making some measurements of stuff.

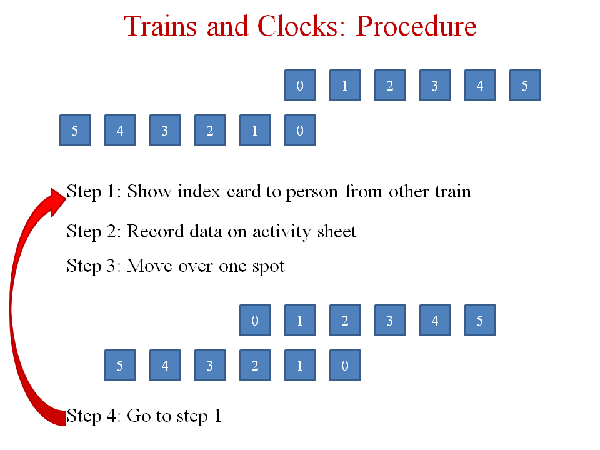
Mermin's scenario as adapted for class is this: you have two trains of six cars passing in opposite directions. Each car contains a narrow window through which the other train can be seen, a clock facing the window, and an observer with nothing better to do than note the readings of the clocks in the two trains whenever the clock in the other train is visible. For class demo purposes, the "trains" were groups of six students arranged in rows facing each other, and the "clocks" were stacks of index cards on which I wrote the times of the various observations. The procedure looked like this:

Procedure for the class activity on trains of clocks.

Students lined up in train-like positions, showed their index cards to their opposite numbers and recorded the necessary data, then moved one spot over, and repeated the process. At the end of the shuffling and moving around, each student had three observations of three different cars in the other train, and the clocks in those cars. From that information, and the information collected by their fellow passengers, they can deduce the rate at which the other train's clocks tick, the speed of the other train relative to their train (by tracking the motion of a single car along their own train), and the length of the other train (by locating the first and last cars at the same instant of time according to clocks in their own train).

This may seem really boring, but in fact they got weird results:

1) Every observer in every train saw the clocks in the other train ticking at a different rate than the clocks in their own train. (Ten ticks of the other clock to six of their own.)

2) Every train saw the opposite train moving at 1/5th of a car length per clock tick. Which is at least internally consistent, but not the value they would expect-- each train moved one car length every six ticks of their internal clocks, so the relative speed ought to be 1/3rd of a length per tick.

3) Every train measured the other train to be shorter-- all six cars fit between car 1 and car 4 of their own train at a particular instant of time.

Was this just because these were non-science majors who are bad at math? No, it's because I messed with the timing:

The trick behind the trains of clocks activity

The clocks in a given "train" aren't properly synchronized, but are out of step by two ticks per car, as shown in the figure. That mis-synchronization is enough to produce all the strange results, if you're operating on the mistaken but understandable assumption that the clocks in a single train are properly synchronized. Even though each clock on each train moved forward by six ticks between observations, the fact that you're looking at a different clock each time is enough to produce the impression that the clocks are running at different rates. The surprising relative speed happens because the clocks in a single train show different times. And the apparent shortening happens because people who think they are measuring the location of both ends of the car at the same instant are, in fact, making their measurements at different times. (In fact, a bit of thought will show that there's never a step in the passing-train process that has both car 0 and car 5 of one train visible to the other train...)

Why do this? Because that sort of mis-synchronization of clocks is exactly what you get when moving between frames in relativity-- clocks that seem synchronized in one frame will appear out of synch to an observer moving relative to them. And that leads to mis-timing of events, which is enough to produce all the weird effects you see with relativity: clocks running at different rates, speeds not adding in the common-sense way, and moving objects shrinking.

The point of this (really Mermin's point, and Einstein's, and also Peter Galison's in Einstein's Clocks, Poincaré's Maps, which we've read for class) is that clock synchronization is key to special relativity. Once you get the idea that clocks at different positions will necessarily be out of synch according to moving observers, all the rest follows.

How did this work as a class activity? A mixed bag; it would've benefitted from more prep time, but I had a rage-inducing meeting that morning that prevented me from properly working it through. (As it was, I was frantically scribbling times on index cards an hour before class...) The shifting-positions part threw students for a bit, and a couple of groups got their index cards in the wrong order and had to start over. I also had a typo on the handout that threw a bunch of people. In the end, though, most of the groups got the right answers, and seemed sort of puzzled by it. I hope the revelation was illuminating; whether this actually makes the key idea stick in their heads remains to be seen.

Anyway, it was kind of fun, but also chaotic and thoroughly exhausting. I like the idea a lot, though, thus this blog post, to share it more widely.