So, as mentioned yesterday, I got an email asking me about the weird scandal involving the Patriots and underinflated footballs, so I wrote a piece for the Conversation on the subject. since a few people had beaten me to citations of the Ideal Gas Law, though, I decided to bring my own particular set of skills into this, and did an experiment.
[UPDATE: I've added some follow-up/concluding remarks in a separate post from Sunday 1/25. So, if you care about my reaction to Belichick's big press conference, go over there.]
You can see the basic set-up at the link-- I got a couple of footballs from the athletic department and stuck them in the freezer, then used one of the PASCO pressure sensors we have for the intro labs to measure the pressure. For a popular article, of course, I didn't go into much detail about this. That's why I have a blog...
So, the relevant physics here is the "Ideal Gas Law," usually written:
$latex PV = nRT $
In this context, P is the pressure in the ball, V the volume of the ball, T the temperature, n the number of moles of gas inside the ball, and R a constant to make the units work out right. This says that the product of pressure and volume is proportional to the amount of stuff inside the ball multiplied by the temperature, and is one of the founding equations of the subfield of thermodynamics.
Something like a football is made of fairly stiff leather, and once it's mostly inflated, it really doesn't change volume very much. Which means that unless you let air out of the ball, reducing n, the pressure is proportional to the temperature. If you decrease the temperature, you decrease the pressure, and vice versa. This leads to all sorts of fun effects-- my favorit silly example is that little curl of mist you see at the lip of a freshly opened bottle of beer in tv commercials. The beer inside the bottle is under pressure, and when you pop the cap, the pressure drops suddenly, which leads to a corresponding decrease in temperature. And, if you're in a somewhat humid environment, that produces a little mist as water vapor in the air condenses.
For the case that's producing my current fifteen minutes of fame, what matters is the pressure change that comes from a change in temperature. One possible innocent explanation of all this might be that the balls were inflated in a warm place, then the game was played in a cool place, and the pressure decreased as a result. So, how plausible is that?
Well, you might say that the temperature change is pretty substantial, even for a relatively warm game-- if it was, say, 75 degrees inside, and the game was played in 50 degree temperatures, well, that's a change of about 33%, right (25 degree drop out of 75 degrees to start)? The problem is, those temperatures are in Fahrenheit (America, f&*k yeah!), and we're talking about physics. the temperature that matters here is the temperature in Kelvin, measured starting from absolute zero. In which case the change is just about 14 degrees out of nearly 300. Not nearly enough to produce the 15% change in pressure found by the investigation.
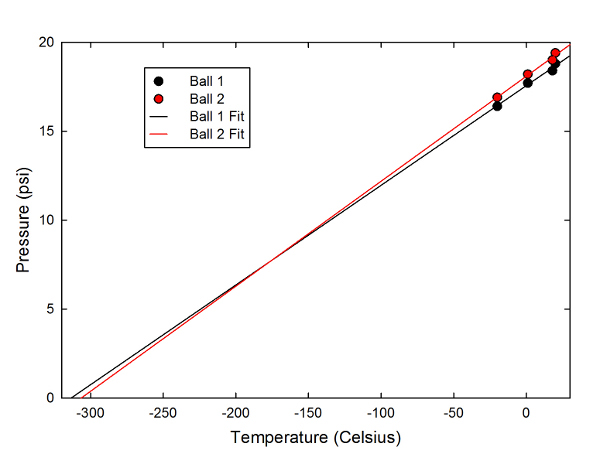
But a bigger change, like from my simple freezer experiment, can show a significant change. Since it's not science without graphs, here are some graphs showing the data from the two balls:
There are four data points here: The initial pressure in the lab before the experiment, the pressure after spending a night in the -20C freezer, the pressure after spending three hours in the crisper drawer of the fridge, and the pressure after warming back up to room temperature. I've plotted these versus the temperature in Celsius, though I've mixed unit systems by measuring pressure in pounds per square inch, since that's the unit used by the NFL (America, f&*k yeah!).
As you can see, the pressure measurements for the two balls fall nicely on two slightly different straight lines, reflecting the slightly different starting pressure (the balls were flat when I got them, and I inflated them using the battery-powered compressor in my car, whose pressure gauge isn't designed for inflating footballs to pressures below 20psi...).
Looks pretty good for the Ideal Gas Law. So, what else can I do with this? Well, I can fit a straight line to these, and work out the value of absolute zero-- the Ideal Gas Law suggests that as you continue to decrease the temperature, you should eventually hit a point where the pressure goes to zero. This defines the origin of the Kelvin scale. And, in fact, this is how absolute zero was first determined, more or less-- by measuring the pressure vs. temperature for a bunch of different gases over a wide range, and extrapolating to zero pressure.
So, the lines on the graph above are just that: the results of a linear fit to each of the data sets. From these lines, I can work out two values of absolute zero, and get -314 and -307 Celsius, respectively, with an uncertainty of around 29 Celsius. The actual official value is -273.15, so this is pretty good. I'm a little surprised at just how well that worked, to be honest, as air isn't really an ideal gas, and the volume of the football isn't perfectly constant, and the temperature range I could access easily isn't that large. But, yay, thermodynamics.
Of course, it's also a little inelegant to have those two lines on there, since the Ideal Gas Law is supposed to be a universal principle. So, I also did a very physicist-y thing, and made a "normalized" graph. The idea here is that I don't actually care about the exact pressure, or volume, and I definitely don't care about how many moles of gas are in the ball. All I really care about is the relative changes in these things. So, I can work in terms of ratios of different measurements:
$latex \frac{P_2}{P_1} = \frac{n_2 R T_2 / V_2}{n_1 R T_1 / V_1} $
A little algebra gives (canceling out R, which is a universal constant):
$latex \frac{P_2}{P_1} = \frac{n_2}{n_1} \frac{V_1} {V_2} \frac{T_2}{T_1} $
I call this a very physicist-y trick, because it makes life so much easier-- I don't need to worry about the absolute value of any of these things, or even what system of units I operate in. All I need to do is take ratios-- divide each pressure measurement for a given ball by one of the other values, and divide each temperature (in Kelvin or whatever the stupid system is that uses Fahrenheit degrees but starts at absolute zero) by the temperature for the same point. All of those data points should fall on a single, nice, universal straight line.
So I did that, and:
There are actually two datasets there, but you can barely tell, because the red points fall almost exactly on top of the black ones. I didn't plot a best-fit line for these, but the agreement is excellent.
So, the Ideal Gas Law really does work extremely well. Hooray for physics!
There is one minor mystery here, though, which was pointed out to me in email, namely that there's some ambiguity about the pressure measurements. What you usually measure is "gauge pressure," namely pressure above the ambient atmospheric pressure. So in that case, the pressure inside the ball should be not just what the gauge reads, but the gauge reading plus about 14 psi. In which case, the 2psi change reported in the "Deflategate" story ought to be a smaller percentage change, and thus obtainable via a smaller temperature change. I didn't think of that when I initially did this experiment, but the change I see agrees really well with just sticking these numbers into the Ideal Gas Law. So I don't know exactly what's going on, here-- maybe the sensors I was using were measuring absolute pressure rather than gauge pressure, but that would mean the balls were significantly underinflated, while they were very definitely overinflated, going by the feel of the ball.
So, we'll leave that dangling as an issue to be resolved-- call it homework. If you know what's wrong with this in terms of the gauge/absolute pressure difference, leave a comment and let me know.
[UPDATE: I've added some follow-up/concluding remarks in a separate post from Sunday 1/25. So, if you care about my reaction to Belichick's big press conference, go over there.]
- Log in to post comments


A remark on the open beer bottle and the ideal gas law. We're describing the Joule-Thomson effect, the sudden release of overpressure into a lower pressure surround. In the ideal gas approximation, this doesn't change the temperature. It's likely that the cooling effect is due to non-ideal behaviour, overcoming intermolecular attraction (though note that the Joule-Thomson equations assume no change in kinetic energy).
Why big P for pressure?
........and the conclusion is?
Because little p is for momentum :)
re: gauge vs. absolute pressure - you should be doing your calculations using absolute pressure, which is easy to determine - at sea level, that's gauge pressure +14.7psi (assuming a properly calibrated gauge that can accurately read pressures in the range of football inflation). Of course, you should convert psi to SI units (Pa) for the calculations.
> Why big P for pressure?
Because it's the Patriots. Oh, and tradition.
Yes, assuming absolute pressure a temp drop of 20F yields a drop of about 1 psi based on temperature change alone. Other notes:
The atmospheric pressure was decreasing throughout the game - it dropped about 0.1.
Regarding the colts balls, their pressure drop be controlled by the initial temperature of the air in their balls...or the temperature at the time their psi was checked.
I think a useful experiment would be to take a couple of brand new footballs, inflate to proper pressure, then have a large person kneel on it or otherwise compress the ball, several times, and see what affect that has on the new ball. While it is true, the football is "fairly rigid" it does flex, stitches could stretch, leather could be stretched. Combine that with temp.
Though on point that has not been made, what temp did NFL measure the Pat's balls at before and after. Don't think they measured them at 50 degrees outside, on Monday after the issue arose.
Why big P for pressure? Well, it usually requires gaining some momentum, p, to relieve bursting pressure P by having one large P or a series of shorter p's -- it seems to be at least partially dependent on one's age.
Calculations should be done using absolute pressure and absolute temperature scales. Pressure absolute equals pressure gauge plus atmospheric pressure (14.7 psi). Absolute temperature in deg Rankine equals ambient temperature in degrees Fahrenheit plus 459.67. Using the assumption that volume and density do not change significantly, the ideal gas law results in P/T=constant.
If the balls were inflated at 68 deg F to 12.5 psi gauge and then cooled to 45 deg F, I come up with a pressure change of approximately 1.2 psi.
QED
I think a useful experiment would be to take a couple of brand new footballs, inflate to proper pressure, then have a large person kneel on it or otherwise compress the ball, several times, and see what affect that has on the new ball. While it is true, the football is “fairly rigid” it does flex, stitches could stretch, leather could be stretched. Combine that with temp.
We're actually pretty good at making inflated objects that take some pounding-- bike tires, basketballs, etc. I don't know if the NFL has tested the ability of a football to hold pressure, but I'd be really surprised if Wilson and other ball makers haven't.
Anecdotally, I played rugby in college, which is at least as rough as football, and I don't think we re-inflated the balls we used more than once or twice a semester
Something that occurred to me that isn't being accounted for, possibly, is the heating of the air due to the compression. I know when my local volunteer fire department takes air tanks to the city FD to get filled they always fill, wait 10-20 minutes, top off. This is because the air is pressurized so quickly that as the temperature equilibrates with the air there is a noticeable loss of pressure. Obviously SCBA tanks are at significantly higher pressures (up to 4500psi) than footballs and so the effect would be much greater but could that be enough to effect the results? I'm not sure how you could easily add that to the experiment.
That being said I mostly suspect the accuracy and precision of the pressure gauges used to initially inflate the balls as the culprit. Also, if you were going to purposely under inflate some, but not all, the balls, why 11/12? That seems odd for it being intentional.
Been wondering about this, and you seem to have the only intelligent explanation of this on the internet.
As there are no restrictions as to the temperature of the room in which the pregame pressure measurements were made, if the room was at a hypothetical 90f and not room temp as is normally assumed, then the drop in temp to 50f at game time would be enough of a temperature change to account for 2 psi below regulations if the balls were originally right at the limit. Correct?
Also, wanted to point out NFL balls are different then college balls and this may account for some small difference (If memory serves their volumes are slightly different, materials differ as well) probably insignificant, but worth noting.
"Also, if you were going to purposely under inflate some, but not all, the balls, why 11/12? That seems odd for it being intentional."
Possibly because the 12th ball was elsewhere, e.g. being used to warm up, etc, when the other 11 were "adjusted".
To answer Chad's question, it depends how you considered the initial state of the ball. If the ball was vacuumed to have zero pressure during shipping (a brand new ball from the manufacturer), then the pressure readings used for the ratio should be gauge pressure as the atmosphere is not acting inside the ball(the sealed bladder inside the football is an empty void), the atmosphere is only applying pressure on the external leather surface. Therefore to get a precise pressure ratio in this scenario, gauge pressure should be used.
I was just looking at the set-up again, and the PASCO pressure sensor claims to be measuring absolute pressure (at least, it's labeled "Pressure Sensor (Absolute)"). Not sure I really believe that, though...
If you called it gauge pressure, on the other hand, you'd need to include a bit of a volume change for the ideal gas law to hold. And contrary to one angry dude in the comments at the Conversation, I'm pretty sure the ideal gas law is a good approximation at this range of temepratures and pressures...
There's a cameraman here now about to film me talking about this for a Discovery Channel show. My life is very strange.
This is a problem for 16-17 years old students.
I am surprised to see faulty calculations at comments!
About the pressure measurment:
If you turn on meter at sea level ambient you will immediately check if it measures absolute or relative pressure (14.7 or 0.0 psi)
Foxborough isn't at sea level.
There are a couple of other factors to think about that might have played a role:
1. The inflation temperature might have been more or less than the room temperature depending on how the balls were inflated. With a hand pump or compressor with or without storage tank and what was the tanks pressure and temperature at the time of inflation.
2. humidity - with any level of humidity you have a mixture of two gases (air and water vapor). The water vapor can condense when the temperature changes.
did you design this experiment in a "physics-y" way?
I do not understand why you acllimatized the football to two different temperature states in two different ways? Freezer for a whole night and refridgerator for three hours. This implies that the Fourier Heat Transfer through the solid encasement and the convective heat transfer to the "air" (nitrogen @ STP) for a stable mean kinetic energy of molecules is greater than three hours. Did you verify this assumption? If not, I feel that your experiment was not "physics-y", it was sloppy.
Very good comments. I think the NFL should fine themselves for writing a vague rule and send it to Charity.
They need to specify what Temperature the Ball when measured at and account for air loss for measurements and how many measurements are taken. Did they measure them only once each? Or did they not measure them at all being lazy..
The tolerance on their spec of 1 PSI is stupid with reference to all of the factors mentioned here. Give them another fine.
If they can find some text messages or data showing New England was aware of the P vs T relationship, they might be in trouble for intent, and It will show they lied.
Perhaps the Ball boy knows what pressure Tom likes and set them up accordingly since he a junior physics major who used to work in NASCAR.
Not heard one Media Sports person mention PV=nRT yet. Just sharks in water smelling a kill on Brady.
Brady should wear a headband on Media day with PV=nRT on it, Jim McMahon would just love it.
Rodgers likes a hard ball, I bet they pumped them, up to 13.5 psi and at cold temperatures for the game. We can call that one Inflate-GATE, for Dallas game.
Assume V and n are constants and R is by definition constant...then (P/T)1=(P/T)2=nR/V or P/T is constant.
Using absolute pressure( gauge + 14.7psi) and T in deg. Rankine, a 40 degree Delta T produces 2 psi drop in pressure and a 30 degree Delta produces a 1.5 psi drop. So, we are arguing about a P drop in the footballs that is the same as produced by a reasonable delta T from measurement indoors vs. on the field.
There was an infraction of the rules and that game should not be given to them but we all know that team has a history of cheap , unethical deeds and they pay a few bucks and its overlooked. too bad ==========
\
I like to point out two factors.
The ball was pressured 12.5 psi above atomospheric pressure (14 psi). So the pressured goes up by a factor of two. Then, the air will heat up. The equation is:
T2 = T1 x (P2/P1)^(k-1)/k,
where T2 can be temperature of air inside ball, T1 outside of ball, P2 is pressure inside the ball, P1 outside the bakk, k is specific heat of 1.4 for air. Then, we find that T2 is 60K higher than T1. So, the air inside the ball when inflated could be 130F, which should drop to 50F in the field.
2. humidity
Vapor pressure of water at 70F is 0.61 psi while it drops to 0.1 psi at 50F due to water condensation. After all volume change for vapor from water is x1600. Small hummidity in air can make big change in pressure when it condenses to water. So, here is another 0.5 psi loss of pressure due to humidity.'
Please excuse me as I don't pretend to be a scientist, but the numbers here don't seem to add up. for me If the room where the balls were tested was 72F and the temperature at half time was 45F and the balls were initially inflated to 12.5 PSI, I'm only getting a .63 pressure drop.
My math is 12.5*(45+460)/(72+460) = 11.86psi.
Following this logic, the initial temperature would have to be 140F to bring the pressure down to 10.5psi at 45F. What am I doing wrong here?
Ok, so if all calculations are correct and your saying temperature can change the balls, then the other teams balls must of been with the same amount of air too. Why didn't they get called on their balls being under pressure too? I'm sure the temperature on their side of the field was the same temperature across the other side of the field. I know your calculations look right but once again main subject one teams balls came up under pressure.
Yollie - Colts could've inflated their balls outdoors. Pats could've inflated indoors. Balls tested in locker room. Discrepancy explained.
Why do you trust more? The Colts? Or science?
Do the test yourself - watch a ball drop inflated inside drop in PSI when brought outside.
Chad, in actuality, it drops more than pv = nrt can explain. It comes back up to temperature after an hour inside, proving no air was lost. Why would it drop more than pv = nrt? I just tried it twice.
Also folks - the 12th ball at some fans house right now. Legarette Blount threw it into the stands after scoring a TD.
As has been pointed out here, I calculated that a change from 80degF to 50degF will decrease the inflation pressure from 12.5 to 10.6 psi. 1.5 psi is provided by the ideal gas, 0.4 by the non-ideal gas (water+vapor). All facts that have come out are consistent with this explanation. The long equilibration time you'd expect for the air in the ball confused interpretation of the pressure measurements.
Pump compression heat, rain water being cooler than the surface level ambient temperature, air loss due to Gronking, all would lower the half-time pressure even more.
Thanks Edward. Where do you get 1.5 drop from the ideal gas equation. I only get about 3/4 a psi.
I tried it out with my pump and a football and the pressure drop is in the range you expected. I ran it twice. I encourage anyone else who is curious to grab a pump and a football as well.
NB: equate PV=nRT for the two states.
--> P1/P2 = T1/T2.
Now covert 80F to Kelvin (300K), and 50F to 283K.
P1/P2 = 283/300 = 0.943
P2 = 12.5 + 14.7 = 27.2 psi.
P1 = 25.7 psi, the absolute pressure at 50F.
That's a 1.5 degree difference in absolute pressure.
Subtract off the atmospheric pressure (14.7) to get the gauge pressure measurement. The atmosphere has about constant pressure because it's not constrained by volume, but rather by gravity.
Thanks for doing the experiment. My wife is pleased I don't have to go out in the snow and buy a football.
Edward -
Thanks for the explanation!
I am happy to save you the trip in the snow, but I must admit to being a layperson who has never done an experiment in his life. I've seen some videos on Youtube suggesting a similar drop as well, so that did tell me perhaps my test was fine. I'd love to see a scientist run this experiment with better equipment - I see Chad approximated it, but not sure why he didn't try to replicate it.
NB: Add 14.7 (standard pressure at Sea Level) and start at 27.2 psi.
I would say in the end because all game and attempts after
to replicate the results that are now founded that
we can't say with absolute certainty their was any
pressure letting involved
It will get thrown out
Great article and followup on gas theory, but I wanted to shift focus to the NFL rule, which only specifies pressure, and nothing about temperature, humidity, etc. It doesn't evey specify what type of gas the ball should be filled with. See:
http://static.nfl.com/static/content/public/image/rulebook/pdfs/5_2013_…
With that ball rule as written, a team could deliberately inflate the ball with something other than air, much higher temperature and humidity, so that a gauge reads 12.5 psi 2.25 hours before the game, and still be completely compliant with the rules. The pressure drop by game time does not violate the rule, and the team would only be guilty of using the rules of gas physics to their advantage.
Very quick general reply, because it's the weekend, the kids are rampaging around the house, and my low-grade cold from the last month has exploded into full misery.
I am highly skeptical of most claims attributing this to non-ideal-gas behavior over some narrow range between slightly-too-high room temperature and slightly-lower-than-the-actual-game-temperature, because the data in this post agree very nicely with ideal-gas behavior over a considerably wider temperature range. So whatever's being attributed to water vapor would need to somehow correct itself before the -10F to 34F range I tested in the fridge.
There's also a lot of other evidence that cuts against the idea that this was all just a big misunderstanding, starting with the fact that the Colts' balls apparently didn't have the same problem, and continuing through the reports that the complaint about underinflated balls was first made a week earlier by the Ravens. Yeah, it's possible that some weird combination of factors conspired to push the balls prepped by the Patriots substantially out of the legal zone, but it's a lot more likely that they were doctoring the balls in search of an extra edge, and got caught. The weather might've been a contributing factor, pushing them from not-quite-illegal-enough-to-get-busted into the problem range, but I don't find the attempts to wave the whole thing off remotely plausible.
Chad -
1) The Colts could've inflated their balls outside. For all we know they were sitting out their equipment truck until the team showed up for game day. It's also been reported the Colts started at 13.5. If the Colts knew going in they were going to complain about the Patriots leaving their balls at the minimum to deflate during the game, naturally they were going to ensure their balls were compliant all game.
2) The Ravens complaint about under-inflated balls was actually about the Patriots kicking balls, which are not controlled by the Patriots. I should also point out that reports that this began when the Colts picked off Brady in November have now been called into question. Yet, it remains possible the Ravens are the source of the original complaint given Pagano worked for Harbaugh. Given Harbaugh's previous complaint about the Patriots "cheating" turned out to be erroneous, its not at all ridiculous to think this started with a misunderstanding from the under inflation of the kicking balls. Which yes, could've been quite under inflated during the AFC divisional game which was played in the 15F range.
3) We don't know how substantially out of the legal zone they were. We know what the reports said. The reports also said D'Qwell Jackson felt the balls under inflated. He has since said this was not true.
4) Why not just try the experiment properly? Several people have documented what happens when they take a 12.5 psi from 70 to 40. Do it yourself and see what happens.
I should clarify - kicking balls are controlled by the NFL, not the team. Unlike QB balls.
Inflation-gate
Assumption: Footballs are filled with room temperature air to 12 pounds … what is the on-field pressure reading?
P126.7Psia
T172 degrees F or 295.4deg Kelvin
V1V2
P2Unknown
T235 deg F, or 274.8deg K
P1 V1 /T1 = P2 V2/T2
(26.7)(V1)/295.4 = (P2)(V2)/274.8
Sustituting and cancelling volumes, leaves
P2 = 26.7(274.8/295.4) = (26.7) (0.93) =24.83 psiaor10.13 psig
So down by 2 psi ??? Yep, a normal and predicatable result.
While all our area news folk were standing around and waiting for the NFL to descend from the mountaintop with the judgement on the Pats, a bunch of wet-nosed high school kids did a demonstration of basic science and showed that the Pats did not cheat, and the falloff in pressure is a normal thing attributable SOLELY to temperature change. https://www.facebook.com/PathfinderRegionalVocationalTechni… What is pathetic is the ignorance of basic science displayed by the "Talking Heads"; one would assume at least a single course in General Science would have to be a pre-requisite for college entrance.
I would like to add that to my knowledge, no one can site the source from where the 2psi drop information came from. Therefore, all we know for sure is that the pressure in the ball was less than regulation.
Go to U-tube. Every Tom, Dick and Harry out there are running Tests.
Some better than others, but all same results.
I liked the callout on Psig posted above.
There seems to be confusion on measuring pressure here.
The Rules call out for 12.5 to 13.5 psi. They forgot to add the (G) it should say "pisg".
G stands for Gauge pressure. This means the gauge reference the actual atmospheric pressure at the time of the measurement. this pressure is typically 14.7, and changes based on altitude and weather conditions. ( e.g. Lower pressure front in weather reports )
Psia - is the absolute pressure reference to outer space.
This basic physics is taught in high School, We all should know all the teams are aware of this. The Colts had to be thinking about how they wanted to handle this before the game. What temp was the air when they filled their balls?
Is it against the vague rule to the balls with dry Air?
I would think some teams are focusing on this, would filling the balls with DRY Air, make a lighter football be cheating too? or just being smart?
Maybe Rodgers like a heavier ball and over inflated..... Maybe Packers are filling the balls with a higher content of water on purpose? Is that cheating. Ball boy was just filling them in the steam room. He didn't know, or did he?
Did Patriots understand all of this, YES... Is it cheating NO.
NFL needs to Fine themselves. and fix the rule. Have the Balls go thru inspection, before and after the game.
NASCAR Post race inspections. Sound familiar.
All of this getting real stupid. Go to MLB, How do they handle their balls?
Some Seattle players don't handle their balls so well either and get fined. LOL
Bill Belichick performed science: did an experiment. Documented results. Conveyed those results and methods. Challenged others to repeat his experiment and see for themselves.
Like part of comments in #44 by "Nerd Engineer".
Ideal Gas Law (Equation of State) works because this is a relatively low pressure although we could use anyone of a number of equations of state to solve the problem but first we have to agree on an EOS that will work with non hydrocarbon gases. The pressure gauge used by any of the NFL teams and the NFL Officials is not accurate enough to measure the non-ideal gas effect.
Looking at Dave Borden's # 41 Post, the math is right and i substituted in 459.6 degrees Rankine for the 273 degrees Kelvin (Rankine is what we use here in the US and it works.)
But 0 degrees Celsius (32 degrees Fahrenheit) is 273.15 degrees K or 459.6 degrees Rankine). More than most want to know. Also used a more accepted absolute atmospheric seal level pressure of 14.696 psia.
Using the formula Mr. Borden did with some of the more precise values...
P2(a) =P2=(14.696 + 12)*((459.6 + 35)/(459.6 + 72))
or
P2(g) = 24.838 - 14.696 = 10.142 PSIG
Note: a for absolute pressure
g for gauge pressure
I got basically the same result except that the final pressure was 24.8 PSIA or 10.1 PSI GAUGE.
In agreement that the results are predictable. However, given some of the Patriots' present coach's past behavior like when he paid a $500,000 NFL fine for video taping to get other teams signals; one cannot help but wonder.
Water vapor should not be a problem. I think that a venue in which Pro Football is played will probably have a compressed air system which means that there is probably an air compressor with a surge tank in which the water will drop out. However if anyone wishes to continue that line of discussion of the Ball Boy hand inflating the balls in a steam bath, there is a really neat equation in Keenan & Keyes' steam table book...
Suggestion for the NFL if they even read this: Put the new game balls in a locked sheltered cage out in the elements on the field 8 hours before the game but after the Teams have the chance to play with their balls and prepare them for the game. Have the balls inflated to the proper pressure outside at least 2 hours by the NFL Officials before the game using a small portable air compressor with a reservoir. The officials then allows each teams select the 12 balls they wish to use, after selection the balls are in separate lock boxes by the respective benches, locking the boxes, and unlocking the boxes five minutes before kickoff. Mark all practice balls with a large "W" or "P".
These comments are funny... Pressure & Temperature numbers have to be in Absolute values ( add atmospheric pressure to Gage pressure). Temperature is also Absolute ( add 459.67 to degrees F to get degrees Rankin).
Hey Tom.
My comments about Ball Boy in Steam room was satire....
Belichick did a press conference today and went over all of this, but with a carefully prepared word choices. Got to hear about the handling of the balls prior to giving them to ref for Q/A.
Do we really know what gauge they use? repeatability? time to insert and remove from football. compressor type?
I got a chiller on my air compressor to remove water.
Taking all of this down to the knat's butt is not practical for a leather ball. Going into this amount of detail volume is no longer a constant. football to football variability and more...
From Belichick conference I did learn that the leather might be higher in temperature from surface prep, rubbing, massaging etc. Then they tell Ref what pressure they want, that being 12.5 PSIG. Sounded like refs are filling and measuring in their locker room and after that they go out to the cold area.of the field.
If they punish Belichick that he knew all of the physics ahead of time, then we got to look at Colts. They got preped from Ravens, and prepared their balls to deal with this.
Guess they knew it too. So what if the Colts planned to have Brady with Low pressure balls in 1st half, then bring all of this up, so then they change the feel in Brady's football to throw him off in 2nd half? Is this a cheating strategy? Why didn't Colts bring it up before game , why wait till half time? hummmm.
This is not a technical issue, it's a political on. Going to be interesting to see if NFL figures it out. White Tip Sharks still want Brady Blood. they smell it in the water...
If you guess are into pressure measurements, Let's talk vacuum, much more interesting. Think Torr not Psi.
Hot cathode, cold cathodes, thermocouple, ion, spinning ball, etc. much more interesting gauges to choose from.
For the ideal gas law to work, you must use absolute pressure and temperature. For degrees F, add 460 to the ball temperature. With a pressure gauge, add the gauge reading to the atmospheric pressure at that location at that time. This changes with elevation, constant here, and the barometric pressure, nominally about 14.7 psi, but look it up for Gillette Stadium at half time. You may have to assume the volume doesn't change, since calculation of the volume change in a football with temperature and pressure would be very complicated. Or, fill a new ball at 80 degrees locker room temperature to 12.5 psi (the minimum per the rules) and then wait for 40 degrees temperature in Foxboro, and then measure the pressure again. A quick calculation with some assumptions shows you COULD drop the pressure 2 psi. The calculations: (460 + 40)/(460+80) =.926 and a storm moved in during the game (which it did), we will use a low of 29 in mercury, or 14.2 psi, so 14.2/14.7= .966. Multiply those two together and you get 0.89, or an 11% drop. Again ratio absolute pressures and .89 x (12.5+14.7) = 24.2 absolute pressure; subtract 14.2 absolute at the time and, voila!, you get 10 psi, or more than 2 psi low.
I am fascinated that the rule book puts the balls under the control of the referees for two hours before the game.
Many facts remain at issue. Was the pressure 2 psi below 12.5 (hence 10.5 psi), which is my interpretation, or 13? It has been reported that the pressure was low at half time and the ball pressure corrected by the refs. Was that the time they were 2 psi low, or were they also low at the end of the game? Big difference, given how the 2nd half went!
The Pats said in the last press conference that they repeated the temperature conditions and got a drop of 1.5 psi just as Chad's analysis suggests. If the balls were found to be at 10.5, that is an admission that they cheated by starting with them at 12 psi.
Some claim it would be impossible to drop the pressure on the field. Clearly they are unaware of the existence of a "bleeder" gauge that will allow you to screw on a needle for measuring the pressure of a ball. A few seconds, and you could do it a half psi at a time.
I would hope the NFL uses a gauge like is used to set the pressure of 6 psi drag tires for competition rather than a stick gauge designed to measure 120 psi truck tires.
Side comment:
In my experience, any measured pressure without an extra annotation on the units to indicate absolute (such as psia, kPaa) is assumed to be measured with a gauge. Unreal situations, like textbooks, tend to vary. People who pay attention to details (e.g. some engineers) don't leave this distinction to the eye of the beholder and use psig and psia every time.
PS - Helpful factoid. At the much higher gauge pressure of car tires, the pressure drops about 1 psi per 10 deg F. My dad taught me this, and to always check tire pressures when winter rolled around.
"If the balls were found to be at 10.5, that is an admission that they cheated by starting with them at 12 psi."
CC Physicist - I am afraid you are mistaken. The rule states it is the sole responsibility of the officials to bring the balls out at no less than 12.5 after the team has delivered the balls to them. If the balls were at 12 psi to start the game, that is purely on the NFL officials, and no one else. Aaron Rodgers has admitted they like to overinflate their balls past 13.5 before handing them to the officials to see if they will catch it. That is not illegal, or cheating. Again, the rule explicitly puts the burden on NFL officials.
I am afraid this thread has some good science, but the football knowledge, even from Chad, is sorely lacking and full of misinformation.
FWIW - an independent lab ran an experiment that does show PSI drop nearly 2 PSI by replicating conditions from last Sunday:
http://www.headsmartlabs.com/#in-the-news
Which is exactly what every person who has taken a football and tried it has found.
If the balls were inflated at room temperature and the game was played at zero F would you should see a drop of approx 1.6 psig. But, the temp at game time was 51 F which would result in a pressure drop of 0.43 psig. If, by halftime, we assume that the temp had dropped 10 degrees (I'm sure someone would know what it actually was), then we should see a drop of about 0.7 psig. Either way, if the balls were inflated only to the minimum at room temp, then it is likely that there would be a decrease below standards by halftime.
BUT, the better question is why is each team allowed to provide its own game balls? Surely there should be sufficient quality control so that a complete set of footballs can be provided to officials with sufficient standardization for there to be no significant difference within a game or even between games. Each team plays on the same field and each team should play with the same footballs.
> divide each pressure measurement for a given ball
> by one of the other values, and divide each temperature
> (in Kelvin or whatever the stupid system is that uses
> Fahrenheit degrees but starts at absolute zero
>
That's the Rogain temperature scale. It was developed by some balding guy who kept getting a cold head.
Use of the Ideal Gas Law assumes constant volume. Not a bad assumption. However, if you have ever handled an under-inflated football, you know that the ball flattens somewhat - a lot if the ball is highly underinflated. I think in the case of going from inflation in a warm room to a cold playing field, we would see both reduced pressure and slightly lower volume.
I should add the obvious to the above comment. That is that reduced volume would lessen the reduction in pressure. To some extent, we have a balloon here. The elasticity of the "balloon" complicates things significantly.
It's not quite true to say that the ideal gas law assumes constant volume-- it's perfectly possible to put in a different V along with a different T. It's just simpler to think of it as a constant volume.
In fact, there's a very small but consistent deviation from the ideal gas law, in the direction of slightly higher pressure. If you fit a line to the normalized data, you find a non-zero intercept. This could be due to a smallish change in the volume of the ball-- a decrease on the order of a percent or so-- but that's probably within the uncertainties of the pressure and temperature measurements, so I didn't bother trying to include it.
Sorry for typos etc in past messages...
The HeadSmart Labs report was pretty good, just ran controlled tests for Data.. I'll have to see if I can find that gauge from picture and see what it's specs are.
The Wet footballs adding to a [ 0.7 psig ] reduction is interesting. Sounds like a change in volume is in the works.
Perhaps they need to do some volume measurements, a water displacement in a tank I'm thinking. maybe in a thin plastic bag.
Mass measurements would be good idea as well.
It is also interesting that that is no information on any changes in pressure to the 12 Colt Footballs? hummmm.
Skipping this information helps the narrative, of the attack on Patriots. No Data, that leaves most of the folks ASSUMING there was NO CHANGE in those 12 balls..
All these "Drive-By Sports Journalist" sure don't ask that question. Interesting, thought they were covering this story....
Where is the Data? If those balls only went down 1 psig to still be in regulation specification, that is strange should have been higher delta P.
What tricks did the Colts Do? Where are the cries to know what they did in tampering with their balls to not be impacted by Mother nature?
What are the regulations on what they can apply to the balls to get them game ready??
If the ball were wet, would the ball's leather, and rubber bladder inside it, not expand, further reducing pressure by increasing volume?
Seems like a stretch that a 30 degree temperature drop (75 to 45) will lower the pressure 2 psi. If that were true balls played in 15 degree weather, a 60 degree drop, which happens quite often in places like Green Bay would always be way under pressure.
But let's imagine you wanted to get a 2 psi drop. Cool the balls down, load them up to 13 psi with air heated to 130 degrees, give the to the refs to measure, two hours before the game, and by game time... voila.
@Jack K.: "Seems like a stretch that a 30 degree temperature drop (75 to 45) will lower the pressure 2 psi."
So you're refuting the science because it *seems* wrong?
Dave Borden’s # 41 is correct - weather can and does completely explain the lower pressure.
The pressures specified in the NFL rules, 13.5 to 12.5 psi, must be relative (gauge) pressure because the absolute pressure inside the ball must be greater than the outside air pressure of 14.7 psi otherwise the ball would not be inflated at all. So the pressure inside the ball has to be greater than the atmosphere pressure of 14.7 psi.
Such a waste of time and energy spent over errors by "experts" .
The Patriots are innocent and those who didn't believe owe them an apology at the very least.
Just a side comment on the little cloud above the bottle top when the cap is flipped: it's just a matter of expansion of the gas above the beer and below the cap. As the gas expands, it does work on its surroundings (the overlying atmosphere), and thereby loses thermal energy. It's just the opposite of the heating of the base of your bicycle tire pump: in that case, you're doing work on the gas, thereby increasing its thermal energy. When a parcel of air in the atmosphere is made to rise, it expands, owing to the lower ambient pressure, and it cools. That's how clouds are formed!
What would be the effect of barometric pressure on this equation? Not only would there likely be a large difference between air pressure in a central air system to outside, but the barometric pressure dropped significantly between 4pm (the time of initial inspection) and 9pm (halftime). According to the following weather data it went from 29.89in - 29.61in. With the storm system starting to pass through during the first half.
http://www.wunderground.com/history/airport/KOWD/2015/1/18/DailyHistory…
Per PFT:
"But what was the NFL really found? As one league source has explained it to PFT, the football intercepted by Colts linebacker D’Qwell Jackson was roughly two pounds under the 12.5 PSI minimum. The other 10 balls that reportedly were two pounds under may have been, as the source explained it, closer to one pound below 12.5 PSI."
So the ball that went through the Colts sideline was 2 psi under.
The other ten balls in Patriots were 1 psi under.
That would put an end to this thing as far as I'm concerned - and, if anything, require the league look into whether the Colts even truly believed there was subterfuge going on, or whether this was just gamesmanship to get under a rival's skin.
Not confirmed yet, but neither was the 2 psi under for all 11. Being 1 psi under is perfectly explainable by science. We know it would lose some psi. It's ludicrous to suggest a ballboy would take out some small fraction of a psi. If you've felt the difference between a 10.5 & 12.5 psi ball, it is completely imperceptible. 12.5 to 12.2 or something like that would be silly beyond belief.
As leather becomes wet it becomes more elastic. Thus V is not constant during a game played in the rain. If you watch the Pathfinder Regional Tech video you will see how the PSI drops much more rapidly than you would expect from the usual Ideal Gas physics calculations. I believe the real-world test done at Pathfinder shows the effect of the elasticity change from dry leather to wet leather.
Still have not seen any data on what pressure was in Colt balls after 1st half?
Were they measured?
Was data published?
Game Stat: Time of possession
Colts = 22:11
Pats = 37:49
Did not see breakout for 1st half. Most of the Colt balls never saw the playing field and rain/water factor. An assumption, I know.
NB@51:
Perhaps I should have said "trying to cheat", as with the Aaron Rodgers statement about pressures. We don't even know if the referees checked the pressures before the game. And the rulebook does not say they must raise the pressure (or drop it) just to the limits specified in the rules; they could set them all to 13 psi within the rules, but probably do not.
Regarding the pressure drop to be expected, many different temperatures could be used. I followed what the Pats seemed to think was the situation when using 1.5 psi.
NB@64 as well as 51:
The rules also don't say that a team cannot change the pressure during the game, only that a ball below 12.5 psi or above 13.5 psi is not a legal ball. That means any ball outside that range should have been immediately removed from play at half time, not reinflated, and every ball mentioned in your comment was illegal when used during the game. Per rule, the refs could possibly choose to adjust the pressure of the extra balls provided by the home team, but they could plausibly reject any of them as well and force the Pats to use the visitor's balls.
CCPhysicist -
There is nothing in the rule book about measuring the balls after pre-game, or ensuring they are within legal limits during the game, and taking them out of play. Nowhere does it state that the burden is on the team, or the official even, to ensure that the balls remain within the legal range during the course of the game.
As far as I know - and as echoed by Bill Belichick yesterday - never in the history of the NFL have balls been measured during a game. And you cannot possibly tell me that a ball hasn't dipped below legal during a game. In fact, just the prior week, I am certain that both the Ravens and Patriots were playing with balls that would be deemed illegal if they were checked.
In fact, I should point out that during a Vikings-Panthers game earlier this season, when the ball boys were trying to warm up the balls due to the 12F temperature, the league explicitly said they were not allowed to try and heat the balls back up.
http://espn.go.com/blog/minnesota-vikings/post/_/id/11218/nfl-aware-of-…
In this case - the league is making clear: not only is there no burden to keep the balls within legal limits of PSI, it would be against the rules to try and do so. Naturally no discipline was handed out because as recently as November, the league didn't give much a hoot about ball PSI.
So, no, your summary is completely inaccurate. Balls are not to be removed from play if they fall under 12.5 psi. What happened Sunday night was a first in the NFL - an unprecedented, and now seemingly unwarranted action.
It is now coming out that the driving force behind testing the balls is former Jets Director of Operations and current NFL VP of Game Operations Mike Kensil, long a Patriots rival. How convenient that on the weekend the Patriots launch a tampering charge against the Jets for Johnson's comments on Revis, a former Jets employee suggests something that's never been done in the history of NFL: take a ball out of play and test its PSI.
Again, there is no rule, you are mistaken.
One reason no such rule exists is that because it would be impossible to implement in a game that is played outdoors, in the elements, often in cold, rain, snow, where day turns into night, etc. Another reason no such rule exists is because no one gave a flying crap about ball PSI until last week. In fact, I should remind people that all this stuff isn't even in the NFL rule book. It's in the game operations manual.
Football is played in the elements. Balls are going to lose air in winter games. That's part of the game.
https://www.youtube.com/watch?v=_Gd0kGhIcF4
This is the Link to that video Wayne mentioned. I do like this test.
As all of this goes forward, and some calling a test not accurate for a 50 - 51 Temp difference, the plunging of the ball in the water to get lower temp doesn't mimic game conditions. That being said, the ball was not allowed to achieve equilibrium in temperature either. The Test does show as stated earlier that there is merit to all of this dialog.
Where are all the tests to explain why the non published Colts football data didn't drop in pressure? How were those balls prepared / tampered with?
I also got a good laugh out of one news article. They claiming this was never a problem before, in worst weather conditions, as if they have always looked at this in detail. his whole point was to knock Brady down a few rungs.
How about some chemistry. mixture/solutions and reactions.
You mix some "stuff together" and want the reaction to go faster, you add a catalyst.
Colts/Ravens were the catalyst in this one to get the reaction going. Didn't see no catalyst in the Cowboy/Packer game......
I guess the weather was a non factor in that Game, someone forgot to add the catalyst to that mixture.... LOL
No one here has given Laser physicist (post 25) credit for pointing out that as you inflate the football, as the pressure inside it goes up, so does the temperature!
That's right!
The temperature of the air inside the football goes UP when you increase the pressure by inflating the football!!!!
(Rembember PV=nRT.)
So the temperature of the air in the ball right after it is inflated is not room temperature!
Laser physicist calculated the temperature of a just inflated football to be temporarily 130 degrees F.
Now I am not sure if it really goes to 130 degrees, but it seems obvious the temperature in the football goes up as the pressure goes up.
Fairly quickly the temperature of the air inside the football would cool down to air temperature.
And guess what!
As the temperature INSIDE the football goes down fairly quickly over time, the pressure inside will fall - even if the game was played at room temperature!
Why haven't others commented on this?
Good thought - thanks Charlie for drawing our attention that.
Laser physicist in post 25 points out that as you inflate the football, the temperature inside goes up as well.
This is just a simple application of PV=nRT.
Let me repeat it, because no one else has commented on this.
As the pressure in the football is increased during its inflation, the temperature of the air in the football also goes up!
Laser physicist calculated the temperature should go up to 130 inside the football temporarily.
I don't know if this is how warm it really got, but certainly the temperature inside the ball does go up as it is inflated.
Then, as the ball sits, it will radiate heat - and the pressure of the air inside will go down.
So my presumption is that the Patriots started with an under inflated balls, pumped them up to the league minimum, and gave them to the officials.
I doubt anyone filling up the balls knows anything about PV=nRT, or that it could be expected that the pressures will be going down as the ball radiates the heat caused by inflating it.
Would anyone care to comment on this?
You also have to account for the slight (but non-zero) change in volume, since the ball is not a rigid vessel.
And a football that becomes wet during the game becomes an even LESS rigid vessel as the leather becomes more elastic. Anyone out there who can calculate what the % increase in ball diameter would be required to drop one PSI?
Charlie (Post #70)
Good point Charlie and you are correct. The actual numbers for increased Temp can vary thou. If the Balls were just topped off with Air, a smaller Delta-T. If the Balls were completely filled it would be more.
Not knowing actually what happened, my guess would be the Balls were close specified Temp and minor changes would be minimal.
Physics behind this is sound.
(e.g. When a SCUBA Tank is filled from say 500 Psig to 3000 Psig , it is placed in a tank of water to increase heat transfer rate )
I wonder if any of the NFL teams totally deflate the balls and then fill them back up just prior to giving them to the refs?
On Laser Physicist equation
//"T2 = T1 x (P2/P1)^(k-1)/k"
Sorry for the silly, question, but what assumptions in this problem would forbid us from using T2=T1x(P2/P1), i.e., if we take PV=nRT and work the problem at constant n and V?
Work the math for a steam room at 110 F. With water vapor and temperature change it seems to match the 2.5 psi drop at 45F.
The Specific Heat ratio of Air is not constant either. It does vary with pressure too. I know it's super tiny difference....
http://www.engineeringtoolbox.com/air-specific-heat-various-pressures-d…
n is not constant (maybe based on measurement method)
V is not constant either, the wetness of the ball and effect on the leather.
lots of this stuff getting talked about become 3rd and 4th order effects. Thusly neglected.
If we really want to go into other low order effects on Ball Pressure, you have to add the fact that the internal air molecules will pass through the football. Before I get jumped on... Think about if the ball was filled to 13 psi and kept in a controlled environment for say 50 years. The pressure will be less.
For this problem, easy to call it a non effect, but it still is a factor being ever so small.
This is where you go when you peel the onion back too far.
Thanks Nerd Engineer for replying.
I'm not sure either if the Pats just "topped off" the ball to reach 12.5 psi, or if they started with fairly deflated balls.
Still, all of the following seem to easily add up to why the ball could register lower than 12.5 psi at halftime:
1. Increase temp in ball when inflated, then having the ball lose that increased temp as heat was lost to the environment, thereby leading to a decrease in measured pressure.
2. Outdoor temp of about 50 F at halftime leading to a further fall in internal pressure in the ball.
3. Falling barometric pressure as the storm intensified.
4. Wet leather allowing the ball to stretch more, leading to a lower internal pressure.
While all the calculations done by posters was vital to understand why there likely would be a fall in pressure, science always involves doing the experiment to prove if the theory is correct.
(And all would agree that "air" is not an "ideal gas".)
The testing in the above posted video from Headsmart Labs
shows how easy it would have been for the NFL to scientifically verify that there is a very likely reason why the ball pressure was less than 12.5 psi.
Now, where do the Pats get back their reputation?
CharlieinNeedham says "Now, where do the Pats get back their reputation?"
Answer: They Don't , that's the point of all this.
1st order factor : ( the battles between Jets and Pats )
Still can't find any info on what the Colts balls were measured at..... no data so "drive-by media" says there was no changes at all.
They sure did find that Comment about Brady like a ball lower in pressure from Gronk spiking it thou.
Duke lacrosse Team. What happened there. still guilty.
Darren Wilson, same deal.
Factor are interesting and can be used as needed to make your point. Facts that don't, not facts at all.
Falling barometric pressure increases the gauge pressure.
NB@68:
The rules in the link cited above are quite clear about not using a ball that does not conform to specifications.
It wouldn't surprise me to see some additional regulations added in the future. That is what usually happens when someone is suspected of finding a loophole in the rules (which in this case are vague about what the referees are supposed to do if they suspect a ball has been tampered with) for most sports.
CCPhysicist -
Please explain further. The rules I have read have made clear that no one is to alter the balls after ref inspection.
Additional regulations will be added - but they will be unnecessary and only done to justify the NFL's investment in this investigation. I can assure you football coaches & players could care less about PSI, other than the three organizations involved in questioning the Patriots here. The mood at the Senior Bowl this week was bemusement over the whole thing.
A couple of points:
1) Interesting idea that the temp of the air at inflation is high, but probably not so relevant since they were likely inflated long before so they could be properly worked in during the prior week.
2) Everybody talks about the game time temp at 51F, but I haven't heard anybody say the half time temp (an hour later) when the supposed measurements occurred. A 25 degree F drop from 72 to 47 is a 4.7% decrease in temperature on an absolute scale. A 4.7% decrease in 27.2 psia (12.5 psig) gets us an anticipated 1.3psi drop according to the ideal gas law.
3) Game time humidity was reported as 71%. At 100% relative humidity at sea level air is approximately 4% H2O molecules. [.7 * 4% approx equal .03] So, we could get up to a 3% reduction in pressure as the H2O condenses as the temperature drops below the dew point. My calculator shows game time temp at about 7 degrees C below the dew point. Since relative humidity increases by about 5% per degree C, the air in the ball would be expected to be approx 135% saturated. In other words about half of that 3% could condense out, leaving 1.5% reduction in P. PV=nRT. n decreases by 1.5%, so P (27.2 psia) decreases by 1.5% = .4psi.
1.3psi + .4psi = 1.7psi reduction anticipated.
Any experiment that deviates from this number has some esplainen to do, baby.
re: humidity
Thought about this a few seconds more and realized that I'm probably understating the impact of humidity and condensation. As the air pressure is almost doubled from 14.7 to 27.2, the partial pressure of the water vapor is going to double. Pressurized air is generally likely to be fully saturated unless the pump has a dryer.
The referenced video on officials filling the kicking balls showed them using a small cheap pump that certainly did not include such.
Bottom line: humidity is consequential, too.
If ball was measured in a 70 degree room both times would the temperature on the field matter?
As the ball becomes fully inflated, the increase in pressure becomes larger with smaller volumes of air. Just like with a bike tire, the force required for the last pump of air makes it difficult as the pressure rises exponentially.
Has anybody calculated what the volume change is from 13.5 to 12.5 to 11.5? I suspect it is tiny if most people and officials can't tell the difference by feel.
Halftime is very short, I doubt the ball inside the football could come up to temp with the locker room it was tested in. The air inside the football would've been outdoor temps. Someone correct me if I'm wrong.
NB,
I think you are absolutely correct that since halftime is so short, there is no way that the temperature in the ball would have come up to room temperature, even if they did bring it inside to do the pressure testing.
"more physics" Nice work.... The humidity is a bigger factor than most would think. I dump a 1/2 cup of water out of my chiller every other day or so, and got a pulsed water purge on the tank as well.
The boys out there that don't think it's an issue, go drain your compressor tank. If you live on southern border of Arizona, probably not an issue.
The Refs had to have done halftime checking/ filling on field or just inside to get out of rain. No time for Balls to get to Equilibrium inside. They would have got it done ASAP as well, so right when halftime started. Balls would still be cold and wet.
They went inside to get out of rain, no clue about effects on ball pressure. But we still don't know what they did.
"Lots of Assuming going on out there".
I still get a Kick out of Rule wording for ball to be at 12 1/2 to 13 1/2 pound ...... Sounds like weight with poor wording.
Going by Rules, you could fill the balls with Helium and still be fine....
http://static.nfl.com/static/content/public/image/rulebook/pdfs/5_2013_…
The reason the rule is vague and inadequate is because no one has ever cared about this stuff to this level in the history of football before. Aaron Rodgers brags about over-inflating balls and doesn't get fined. The league sees ballboys warming up balls to keep them from going flat during a Vikings-Panthers game and issues no punishment, merely a reminder of the rules.
Ironically, it now appears very reasonable that the Patriots did no wrongdoing, yet they have already faced a punishment - a beating in the court of public opinion which undermines their accomplishments.
more physics,
I wanted to comment on your statement:
"Interesting idea that the temp of the air at inflation is high, but probably not so relevant since they were likely inflated long before so they could be properly worked in during the prior week."
However, since the Patriots seem to have wanted the balls at 12.5 psi (the minimum allowed), they probably waited until just before giving the balls to the refs to check/inflate the balls.
Since they like relatively low pressure balls, the likelihood is that the balls just before game time were low, since the last time they inflated them the pressure would have fallen as the temperature fell from the initial inflation.
Thus it is very possible, that they "topped off" the balls by inflating them up to 12.5 just before sending them over to the refs.
It is also possible that since these were to be new game balls that they came fairly "flat".
(That is how every football that I have ever bought comes.)
So they may have inflated them to 12.5, then "roughed them up" like every team does so the quarterback can get a better grip , then sent them over to the refs.
Mike Florio is reporting on NBCSports.com that the only ball that was about 2 psi under inflated was the intercepted ball.
The other 10 balls were only 1 psi under inflated.
This would be consistent that the initially tested ball was the coldest ball, and was immediately tested for air pressure.
The other balls were inside for longer, and so may have started to warm up slightly, so they would only be 1 psi under inflated.
(Interesting that after the initial impression that all the balls were under inflated by 2 psi, all but one was under inflated by only 1 psi.)
Charlie - I have also heard that report, but after reading it closely and considering the source is Mike Florio (throws a lot out there, very little sticks), I would take it with a grain of salt. Much like those quick to convict the Patriots based on information from the nebulous "league sources," we, too should be skeptical of any similarly unsubstantiated information.
I think I have read different stories on that Intercepted ball. The player claimed it was soft, then other times he didn't.
Once that ball hit the Colt sidelines, it was in control of who?
Maybe they measured it 1/2 dozen times before sending to ref... who knows... was it tampered with before going to Ref? If so , is that Cheating? hummm.
Big question is why did the Colt balls not have a Delta-P to match the Delta T that has been gone over here so many times?
Did the Colts take there balls to the Field before the game for a lower temp prior to testing?
Then we have all this at half time, no accident.
If the Colts did have their balls at lower Temp before Ref's Q/A, would this be tampering? Playing a game to changing the pressure in the Pat's balls from half to half. Trying to get an advantage? Didn't workout for them, but the intent?
Fines and Loss of draft choices might need to be placed a little differently....
Then again, there might not be a rule saying you can't change Air Pressure in other Teams Game balls...
I know lots of assuming going on. Still don't see any details on those 12 Colt balls......
The player never claimed he felt it was soft. That proved to be misinformation. The difference between a 10.5 & 12.5 PSI ball is virtually imperceptible. Try it out yourself if you have a ball & pump!
@nerd - no doubt you COULD fill the ball with He, but would it make any difference? He in a football is only going to be 5 or 6g lighter which would be pretty much imperceptible from a throwing/kicking perspective.
OTOH, Costco makes a big deal out of filling their tires with N2. From a weight perspective it makes no consequential difference from air, but the benefit is that you aren't pumping in any H2O vapor which becomes fully saturated under pressure leaving you with wet rims and greater pressure fluctuations between cold and warmed up temperatures.
@More Physics - Agree Water vapor the issue. and the nitrogen filling. The balls should be filled with dry nitrogen as a standard. at set temp for filling.
Tires and the pressure much more interesting than Footballs.
As for the slight changes in mass, but you got to understand every tiny moose hair to get any advantage is critical as winning becomes everything.
Look at the level of "Got to WIN" at all cost. The fines and suspensions in NASCAR. Those guys try anything that would give them any little bit of speed. Rules changing all the time, and in detail.
Large Money in winning, large Engineering teams, Drivers that will do anything to win.
Look at how mad they get when they lose. If they had Guns they would shoot each other. Watch Jeff Gordon's fight last year for an example.
Don't think Brady or Sherman or Luck are any different. These guys are wired differently than most.
After all of this shakes out, NFL is going to realize just how expensive this is going to be. They messed this whole thing up big time.
CBravo, you question about the one unaffected ball is easily explained. The kicker cannot have an under-inflated ball. I don't think we need physics to explain particular event.
PDX2008. The rules say the 8 kick balls are different that the 24 game balls.
FROM RULES:
" For all games, eight new footballs, sealed in a special box and shipped by the manufacturer to the Referee, will be opened in the officials’ locker room two hours and 15 minutes prior to the starting time of the game. These balls are to be specially marked by the Referee and used exclusively for the kicking game. "
Here is rule link for your review.
http://static.nfl.com/static/content/public/image/rulebook/pdfs/5_2013_…
Easily the most detailed calculations yet:
https://www.facebook.com/Philtill/posts/10205933079910166
Chad, thoughts?
Its not rocket surgery !
1. Inflate the football using air to the "Brady" (desired) pressure,
2. Inflate the football from the desired "Brady" (desired) pressure to the NFL specified pressure using compressed helium gas.
3. In a short period of time and reduced by high pressure events during the game, the helium will leak past the air valve and thru pores in the leather and stitching of the seams of the ball, until the original "desired pressure" is reached and all of the helium has dissipated into the atmosphere.
4. No trace evidence to incriminate.
5. Now we know why that Ref talks with such a high pitched voice.
The rule should be changed
1. Each team provide deflated footballs
2. NFL official inflate with nitrogen at a known temperature to the specified pressure
Since nitrogen (N2) is 3x larger than helium (H) and does not contain water vapor, the problem is resolved .
When the Pat's coach said that they followed the rules "to the letter", it got me wondering if they may have initially filled the balls in a sauna. Inflating the balls to regulation pressure (letter of the law) in a 150 degree hot box (letter of the law, but not necessarily the spirit of the law) would cause the balls to soften up in cold weather.
As far as kicking an under-inflated ball: Aren't there a half-dozen (different) footballs prepared by each team for kickers / punters?
You guys are overthinking this - the difference in 10.5 v 12.5 psi is imperceptible. SportsScience broke it down, and many people have tried it experimentally, and nearly everyone (Mark Brunell being the exception I have trouble believing) have been unable to distinguish.
Why would the Patriots go through such an effort to bring the PSI level down an imperceptible amount? Football is a very complex game with 53 players a roster, coaching staffs into the dozen, teams have huge play books on both sides of the ball - why would a team devote time and resources to something incredibly trivial and what even Patriots detractors would have to admit would be a higher order term in the outcome of the game (if its a factor at all. I would say it would be 0 factor, realistically).
The most recent report (unsubstantiated of course) is that only one ball showed a drop of 2 PSI. Ten of the 12 balls had dropped closer to 1 PSI than 2 PSI. So the temperature drop from room temperature to 50 degrees would easily account for that change. Unfortunately the NFL "investigators" are looking for a human perp and ignoring science.
NB #101. That was pretty good link to Facebook. Thank you. I asked them a couple questions, be interesting to see what they say. We have beat this horse to death on this blog.
Tim #102 you got my vote to be on rules committee to re-do them. inflate balls on the field 1 hour before game at 50 yard line. Then mix up the 24 balls and use at random.
Molecule Size of Nitrogen (N) vs Helium (He) doesn't matter about containing water. Unless maybe you have a bad supplier of compressed gases.
Im not sure if this has been answered or not but they sat that 10/11 balls or 11/12 balls, whatever the number was that the 1 that was the right pressure, may have been accidentally mixed up with a colts ball. This is a good thread I have been wondering if anybody would think of the science behind it. Of course we want to blame someone because that creates even more viewers of Americas biggest television event.
FWIW Legarette Blount threw a ball into the stands during the 1st half. It has not been reported if that ball was retrieved or not.
The "football rubbing" explanation by Belichick seems NOT to make sense, since when you rub the football it will heat up, and the pressure will go up, not down. But consider this, suppose you inflate the ball to say 12 psi (0.5 psi below the minimum by rule) and then rub it and work it to warm it up and increase the pressure to say, 12.6 psi (maybe even use a hair dryer, naturally present in a locker room) just before you present it to the NFL official for pressure check. After the check, the ball will naturally drop in pressure in the locker room and even more when taken to a cold field. I think maybe the Patriots did this routinely and only got caught this time because the more extreme conditions for this game increased the pressure drop. I'm just sayin'.
There is also the possibility of inaccurate gauges. Were the ones they used calibrated by the National Institute of Standards and Technology (NIST), as is required for pressure vessels? I doubt it.
Ronald - I think that was Belichick's point exactly. They rubbed the balls and filled them. They were filling warm balls, so the temperature drop was heightened.
I don't think he did a great job explaining it, and I think they are probably attributing too much to the rubbing. However, I think they are reporting experimental evidence which can and should be replicated by the league. As anyone who has tried it so far, the ball does drop more than a simple ideal gas calculation, so there is more going on, and it does suggest the Patriots are in the clear.
Unfortunately, the league - which under Goodell hasn't yet shown any signs of competency and is having its worst year in a long, long time - has made up its mind, and I doubt they will even consider science. They will sooner run an experiment to see if someone can deflate 12 balls in 90 seconds in a bathroom before they subject footballs to the weather conditions of the AFCCG and record their PSI.
This problem is actually pretty complicated when one digs down into every little detail. This is why so many technical folks have found it interesting. To make it reasonable you look at just the major factors, The only major factor here is the Delta T (Internal air temperature of the footballs from being in locker room to on the field at half time).
All the other issues and 2nd, 3rd, 4th order factors. To grind out numbers on those, you have to think a little bit more.
The warming by rubbing was explained really well on the FACEBOOK link above imho.
All of the technical folks are making assumptions on various conditions for there is really not much Data to go from.
The Weather reports and barometric pressure numbers are the best, But this is a 3rd or 4th level effect.
If you really want good results, You need to do testing on multiple balls for a good data set and then do some Statistics work on it. You guys should remember the old Gaussian distribution curves, or bell curves from grades in school. same kinda deal...
Now you got the actual numbers, then you can take all of these different concepts and see which one's are most important. This will mean more testing and work.
All of this is ridiculous, Just a stupid football. but kinda fun to review the different laws on nature and effects, and seeing how others look at them.
Heard a story on radio earlier that the Cameras in the stadium had the Ball boy carry the 12 balls from Refs to playing field. He stopped at bathroom and was inside for 90 seconds. Did he tamper with them in the 90 sec period.
(Same 90 seconds NB mentioned I think)
Now we got to go thru the time trials to do all of that in 90 seconds. Say for 1 guy, or maybe there were 11 other guys inside waiting to lower them... Just watch where this goes... If ball boys dropped them 2 psi, the laws of nature drop them another ~1.5 psi, then we got a serious problem of why did the balls have so much Air in them ???
Maybe the Colt Ball boy, stopped by a different bathroom and over pumped the Colt balls, so they could have them at 13.5 psi after the cooling.
Why the Colt balls did not drop in pressure is the real question in all of this? Did they start the game with Over-inflated balls at beginning of game?
Lets see some folks sharpen your pencils and answer that one?
"Why the Colt balls did not drop in pressure is the real question in all of this?"
Seems the only reasonable explanations are either that the Colts overfilled them, or they filled them with air at a lower temperature.
I just want to point out that the balls were depressurized, not deflated, so this should really be called DepressurizationGate...
Dan K. Cool, finally someone sees the real INFLATE-GATE.
Physics: Well that has been rung out here.
Intent: Loser whining -- Ravens, Colts, and Jets (Revis issues).
Planned event: What if Colts would have smoked the Pats in 1st half vs getting their back porches spanked, would they have brought this up?
Trying to win at all cost --- Getting the pressure changed in all of the Brady balls and hoping for the best.
So that being said, Who's playing games here. How about COLT-GATE.
NFL specification is +/- 0 .5 psi, just 1 psi. We all see that it can vary 1.5 - 2 psi. If we went to a colder game, like the Green-bay game be a larger value, all of the balls had to be out of spec there, unless filled at game temperature.
If the Refs inspected the Colt balls and they were cold. Then they didn't break the rules, but shows they planned this. If the Colts gave them 74 F balls for inspections, Then who filled them to get them back up to 13.5 PSI ? Not seen published actual info on Colt balls, but everyone is saying that didn't change in pressure.
2006 - Look at those Boys working those footballs over for Brett Farve.
Not sure I believe any of them on this "nobody know nuffin".
I guess Brett liked his Balls Extra Crispy. ( you see that at end of video )
http://espn.go.com/video/clip?id=12221498
I love it when people use majorly skewed numbers to get the values they want. When you see numbers like 80F and 35F, just through out the comments. Game day conditions were 51F, and room temperature is 68F (although I'd use 74F since that is the usually the highest indoor temp you'll find buildings controlled to). Accounting for humidity results in a drop slightly smaller than 0.1 psi too (although not a 0.4 drop like some have suggested). If we assume the conditions above, then:
Pb (Ball psig) = 14.56 psi (atmosphere at start of game)
Pi = Pb+12.5 (minimum ball pressure allowed at weigh in)= 27.06 psi
To (Temp outdoors) = 51F = 10.56C=283.71K
Ti (temp indoors) = 74F = 23.33C=296.48
Plw (pressure loss from partial pressure of humidity) = 0.1 psi
PV=nRT reduces down to
Pi/Ti = Po/To
27.06/296.48 = Po/283.71
Po=25.89
dP=1.17
P=12.5-1.17-Plw=11.23
It's significant, but doesn't explain the whole story. Also, we have to ask ourselves if they measured the balls outside or brought them back inside for a time before they measured allowing some rise in temp. This is all assuming that the 2 psi drop is accurate though, and that they used the same measuring equipment before the game and during halftime.
The initial leaked information was that 11 of the 12 balls were about 2 PSI lower. The most recent reports have been that 10 of the 12 balls were were much closer to a 1.0 PSI difference. The was one ball that had a 2 PSI difference but that ball had been intercepted by a Colts player and taken to the Colts sideline. We do not know ho that ball was handled but perhaps it was measured multiple times by Colts personnel and lost an additional PSI.
The focus is likely on: is it plausible for science to explain a 1.0 PSI change due to the environmental change? I would say the overall opinion on this forum is yes. Yet it will be interesting to see if the media/public/NFL will allow science to be acknowledged.
There was a very recent NY Times article that quoted a Columbia physicist as saying there was "little chance" that the atmospheric condition could explain the PSI change. I have actually had some pleasant and informative correspondence with the Columbia professor. It was very enlightening to find that the NYT author posed his question as a 2.0 PSI difference (even though the more appropriate question would have been 1.0 PSI) but did NOT acknowledge that value in the actual article. So the Columbia physicist answered the 2.0 PSI question correctly that there is "little chance" you can account for all 2.0 by atmospheric change. However that NYT writer omits the details and manages to infer that the physicist has completely dismissed the environmental conditions as an explanation. Any media bias? Or just media science phobia?
Unfortunately - the latest is that Chris Mortensen confirmed it was 2 psi from his original source. Now, certainly his original source could be wrong. A lot of these guys have been wrong about a lot of things thus far.
I think, without knowing the details, we're better off - for the moment - doing calculations with 2 PSI. If the NFL did all this over 1 PSI, then they are idiots - 1 PSI is completely, absolutely, without a doubt indistinguishable and no team would risk breaking the rules for it. Frankly, I would say the same applies to 2 PSI and everyone I have tested a football with cannot tell the difference. But I digress - I think the 1 PSI under rumor was from Florio and it was more speculation than anything else.
I hope the Columbia folks do a legitimate job with this. No disrespect to Orzel who was the first to approach this thing from a scientific angle, (but did so admittedly under conditions that did not apply): every scientist I've seen who has put real time into this thing has come down on the Pats side thus far. I would assume Columbia would follow suit.
The League has finally revealed that all balls were marked "13 psi" at the 2 hour check inside because they were judged acceptable. It does not even explicitly say that they were MEASURED. (Given all the sleazy talk about calling a bathroom "a different area", and 90 seconds as "some period of time", I am very skeptical what they are saying when the words are "were gauged to be acceptable" without saying "were measured to be acceptable".
There is no data in the history of the league as to what changes occur when balls go outside under various conditions, nor is there any record of what specific pressures were really measured, if they were, until halftime. Furthermore, no rule addresses the question of what pressure they should be when they are being played with, only that they be acceptable 2 hours before the game.
Many so called "facts" were "leaked" by media frenzied reporters, starting with the close friend of the other team's owner. This basically is a farce, and a very poor reflection on the management of the league, who it now seems have been covering their rear end since the Colts presented them with an unprecedented request at half-time that allows no legitimate before/after comparisons with reality.
It will be good for scientists to educate the high-powered lawyers about ideal gas laws for oxygen and nitrogen, condensation effects for water vapor in high-humidity air, changes of pigskin tightness when wet, etc. But the National Football League is paying the lawyers, and they need someone to wipe the mud off their face.
As a Patriot fan I object to this whole unnecessary episode, but as a scientist I can be unbiased and try to educate some uninformed Americans about natural explanations for what happened that are consistent with all the known facts, of which there are not very many.
I found the comments about 13 psi confusing. The officials first say they test to make sure its in 12.5-13.5, then went onto say they put 13 in every ball. I do not believe they put 13 in every ball, nowhere has that ever been stated that the officials add air to as 12.5 or take away from a 13.5 - I am not sure what Vinovich was talking about there.
Also worth nothing the officials never recorded the PSI in either case, just checked for compliance.
"Whatever it is, if it’s in that acceptable range, we leave it where it is. It’s only when it’s either above or below that we have to get it in that acceptable range. We’re confident proper protocols were followed.”
- Right, they did not put them at 13
Bill Skocpol , This whole story is about misinformation and hatred for Pat's and Brady. This is a modern day Lynch Mob.
Out of control "Drive By Media" and the Colts planning this is at the root, IMHO.
Do you really think, the Ref's checking the balls was done with care. They just get past them so they can do something else like have a beer.
This will change in the future and the cost for NFL to deal with it will go up.
Watch this video of the Refs check game balls for Chicago Bears. Note the comments on accuracy, and the high skill at measuring with a low cost gauge. If they could read it to 1/2 PSI, I would be impressed.
http://mmqb.si.com/2015/01/22/deflategate-video-how-nfl-officials-check…
The Tech folks, (with sharpened pencils) working out details of 4th and 5th order effects, and ignoring the 2nd order effect ( the Refs )
Temp before and after is the only 1st order factor.
When you see no one looking at why the Colt balls didn't drop in pressure. Pretty easy to see what this about.
Lets see, the intercepted Ball on Colt sideline, and see if it was tampered with before going with it to Ref. Oh no they didn't do nothing and only checked pressure on the ball some X number of times. Was this still an offical Gameball? Did they tamper with it post Ref inspection. Measuring it once, I would say counts. They had more than 90 secs to mess with one ball... hummmm.
Lots of evidence that is all crap.
NB Post #108 -- I couldn't anything that a game ball got tossed into the stands. If that is true, then their claim that 11 of 12 balls were low is crap statement. That one could have been low as well, but didn't measure it. word choices to make their point.
Nerd Engineer of CA, I'm glad that we have at least bi-coastal agreement on the essence of what happened. And your video URL of how crudely ball pressures are measured and set by the refs before the game sure makes the point that the pressures are lucky to be within the proper range before the game. Even if measured more carefully with two (different kinds of?) gauges at halftime nothing is really known about changes. Remember that the Colts planned to set up the half-time ambush. Their balls very likely were acceptably on the high end before going into the cold and thus still acceptably on the low end given +or- 1/2 psi accuracy at best. Nerd and I agree that the media poured out "evidence" allegedly from the league, that was contradictory, unsubstantiated, and now totally undercut.
If you were a member of the Colts and wanted to lay a trap for the Patriots the easy thing to do is keep your footballs in a cold environment and pump them up to the max 13.5 PSI. Pehaps let the outside leather warm up for 15 minutes before you turn them over to the refs with the air inside remaining quite cold. This way there is a small internal temperature change during the game and a corresponding small Ideal Gas change.
As a material scientist I am curious to have someone quantify the additional PSI effect of wetting the leather. Hydrophylic polymers become more elastic as they absorb moisture. From what I can find leather exhibits the same phenomenon which serves to also lower the PSI as the wet ball swells slightly.
I wonder if the NFL will ever release the scientific proof or will they just say the rules will change in the future with no finding in the current case.
Hi,
Now the media say Bellichick said that the team staff rubs/massages the footballs before a game to break in the new leather of the new footballs.
SO, THEN...what if the team "football massager" rubs the footballs and in the process raises the temp inside them to, say 120 degrees F, due to the friction heating effect. Then, at that temp, checks and inflates the balls to "regulation pressure." IN THAT EVENT, the temp change from "inside to outside" isn't regulation pressure at 75 degrees F to 51 degrees and raining; RATHER, it's from regulation pressure at 120 degrees F to 51 degrees and raining!
I haven't done the calculations--it's been a LONG time since physics class--but would that sequence of events, with the higher starting temp when inflated, result in the witnessed pressure drop by the end of the game???
Thanks,
--Carson
Go to the Headstartlabs.com site and scroll down to the "in the News" section. Click on the "download full report". Detailed experimentation to duplicate the actual conditions was done. They determined a 1.07 PSI drop due to temperature change alone and an additional 0.75 for moisture. Total drop averaged 1.82 PSI.
As a polymer scientist ,I expected to see the moisture play some role in decreasing the PSI as the leather would become more elastic when wet, increasing the volume enough to have an effect on PSI. That plus the Ideal Gas effect yields the answer. We now have hard proof though the less intelligent people will continue to believe what they want and ignore the truth.
P1 = P2 therfore… P2 = T2 x P1
T1 T2 T1
Gay-Lussac's law (from Wikipedia)
Main article: Gay-Lussac's law
Gay-Lussac's law, or the pressure law, was found by Joseph Louis Gay-Lussac in 1809. It states that, for a given mass and constant volume of an ideal gas, the pressure exerted on the sides of its container is proportional to its temperature.
As a mathematical equation, Gay-Lussac's law is written as either:
P ~ T or P1/T1 = P2/ T2
where P is the pressure (Pa), T is the temperature (measured in Kelvin), [and k3 (is the constant from this equation—it is not the same as the constants from the other gas law equations.]
So, if T1 was 75o F and T2 was 50oF, then
75 F = 297.04 K
50 F = 283.2 K
And then P2 = 283.2 x P1 = .953 x P1
297.04
If pre-game pressure was 12.5 PSI, then post-game would be 11.9 PSI
BUT… if the ball were friction-heated (by rubbing) to 120oF before being inflated to “regulation,” then
120F = 322.04K
So… P2 = 283.2 x P1 = .879 x P1
322.04
If pre-game pressure was 12.5PSI, then post-game would be 11.0 PSI
BUT…if the absolute PSI measurements were as listed PLUS 14.7 PSI, standard air pressure (at sea level)
THEN…
P 1 12.5 + 14.7, or 27.2 PSI
75-50 F means: .953 x 27.2 = 25.9; if you subtract 14.7 (gauges neglect absolute factor) = 11.2PSI on dial
120-50 F means: .879 x 27.2 = 23.9; subtract 14.7 = 9.2 WELL WITHIN ALLEGED “CHEAT” RANGE!!!
ARE MY FIGURES RIGHT, OR DO YOU HAVE TO SUBTRACT A PERCENT OF 14.7???
HOWEVER—AND HERE’S THE BIG OH-OH—THAT DOES NOT MEAN NO CHEATING HAPPENED!!!
IF THE BALL TECH WAS TOLD TO PURPOSEFULLY RUB THE BALL UP TO 120o F , THEN INFLATE TO 12.5 PSI AND ONLY THEN HAVE REF CHECK IT RIGHT AWAY…
IT WOULD ACCOMPLISH EXACTLY THE SAME CHEAT AND LOOK LIKE AN ACCIDENT OF CLIMATE!!!!!!
--Carson
DEFLATEGATE CALCS--2
So…if P1 = T1 ; T1 = T2 x P1
P2 T2 P2
And, therefore…
T1 = 12.5 x 283.2 = 1.19 x 283.2 = 337.01K=
10.5
147 F
BUT…taking into account absolute pressures… 12.5 + 14.7 = 27.2; 10.5 + 14.7 = 25.2
T1 = 283.2 x 27.2 = 283.2 x 1.079=305.57K=
25.2
90.4 F
SO…90.4o F should be easily achievable by friction, ahead of ref testing, and not be hot enough to touch to arouse any suspicions!!!
--Carson
This was posted earlier. Some good effort to understand the rub/buffing aspect of this was done,
https://www.facebook.com/Philtill/posts/10205933079910166
The type compressor used to fill the balls is also interesting. If New England was really wanted to have under-inflated balls, they would have sent them in to inspection as warm as possible, AND also under pressured. The Ref's assumed to be using an electric type pump. Get internal Temperature a bit higher.
On the Other side of the coin. If the Colts had say, had their balls at like 15 psi and cold as possible to be above notice. Then the refs lowered them to 13.5 psi Reducing the air pressure would lower internal air temperature. This would help reduce effect of lower temp on Playing field.
Would that be considered cheating? Or is it only the Pat's that can be called out on this.
(e,g, A can of compressed dry air, used to blow off a computer keyboards etc. when you use it, What happens to the temperature of the can? )
How did the Colt balls NOT drop more than 1 PSI from 1st testing with Refs before game till half time?
All I read is that Colt Balls didn't change and Pat's cheated.
The volume of the football is defined by its leather shell. Leather
stretches when wet or rubbed. Shrinks and hardens when dried.
The volume goes as the cube of the linear dimension change.
A 2% change in the linear dimension of the leather would lead to a 6% change in the volume. Abrade and wet a football. Let it dry.
Fill to 11.5 pig at 75F. Rehydrate the leather and measure at 50F.
Actually, it's Charles's Law, not the Ideal Gas Law.
Lots of more leaks and not talking Air pressure. Who knows what real data is....
I heard that most of the balls were just a little under the 12.5 psi spec, and 1 football was down 2 psi.
Wonder if the 2 psi low football was the Ball on Colt side-lines post interception. There should be some video footage of that.
From the assumptions and calculations done, I'm thinking the temperature in the Ref locker room was much lower than estimated.
Lets work problem backwards. Say Temperature change and all the other factors dropped pressure in all 24 balls, 1/2 psi.
Colt balls go down to 13 from 13.5 and Pat balls go down to 12 from 12.5 .
Sounds like the only deflating was done on intercepted ball, but who knows, we need more information and the video of then Colt staff measuring it.
Ravens running for high grass, Don't want their name in this mix..
Brady and crew still getting hammered. I do see some cracks in the attack thou. Cris Carter's veins were pulsing on his head, he sure has an axe to grind with New England. He just knows they cheated.
The "Destroy New England Group" needs to do a change, this one not going their way.
New England cheated by watching too much Seahawk game film. They knew the pattern of goal line offense that they like to Pass/Run/Run in that order. This gave them an unfair advantage on the Seahawks and should be called cheaters for taking an unfair advantage. They might have even known the exact play.
We need some Saul Goodman types to get into that rule book and find a case against them. Maybe they traded for inside information on Seattle playbook. We just know they can't win without cheating. They had to do something. All those wins over the years and all of the cheating in all those games.
Lets switch the title to GOAL-LINE GATE. Maybe Seattle with get the official Win as the Patriots are cheaters.
ROFL