Posted by On Monday, I posed a question to you as to why, when you photograph the Sun at the same exact time every day for a year, you get something that’s shaped like a figure 8, like so:
Image credit: Tunc and Cenk Tezel.
We got a good number of thoughtful comments, many of which are on the right track, and many of which have some misconceptions. Let’s clear them up, and then let’s give you the explanation of what gives us our figure 8, and why other planets make other shapes.
What does the analemma look like at other places on Earth? You can see, above, that (from the ruins) the above analemma is from the Northern Hemisphere. Well, in the Southern Hemisphere (G’day to my Aussie readers!), it looks like this:
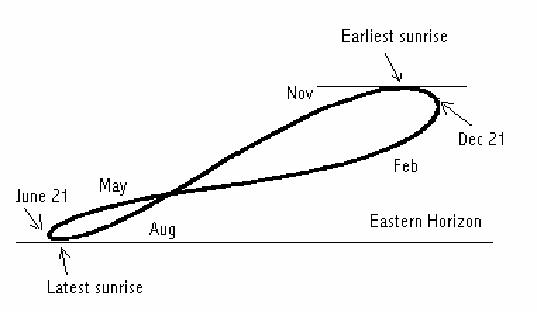
So, at the North Pole, the analemma would be completely upright (an 8 with the small loop at the top), and you’d only be able to see the top half of it. If you headed south, once you drop below the Arctic Circle, you’d be able to see the entire analemma, and it would start to tilt to one side the closer to the horizon you photographed it. By time you got down to the equator, the analemma would be completely horizontal. Then, as you continued to go south, it would continue rotating so that the small loop was beneath the large loop in the sky. Once you crossed the Antarctic Circle, the analemma, now nearly completely inverted, would start to disappear, until only the lower 50% was visible from the South Pole.
So when you do an image search and you find one that looks like this:
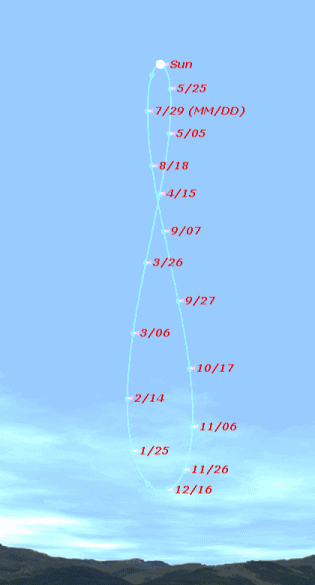
you know that it’s photoshopped or faked, because complete, upright analemmas with other stuff on the horizon aren’t completely visible from Earth! The only exception? If you photographed the Sun at exactly noon every day and never did daylight savings time. But in that case, you should get a picture of the sky, not of the horizon. (So beware of fakes!)
So, now that you know what it looks like everywhere on Earth, you’re probably thinking that this analemma has something to do with the Earth’s axial tilt. In fact, many of you guessed that that plays a role. You’re right! You see, the Sun always traces out a nice arc through the sky, like this series of pictures taken during winter solstice from the UK:
Well, as winter transitions into summer, that arc gets higher and higher in the sky, peaking at its highest point during the summer solstice, and then declining back down to its low point as summer transitions back into the winter. The Earth’s axial tilt — responsible for this phenomenon — explains why the Sun moves along this direction (drawn in white) of the analemma:
So on a planet like Mercury, where the axial tilt is less than one degree, the Sun’s position in the sky doesn’t change from day-to-day, and so an analemma on Mercury is just a single point! But something else must be going on; Mars, which has almost the same axial tilt as Earth, has an analemma that looks like this:
So something must be going on that allows for variations in shape. Some planets see ellipses, some see teardrops, and some see figure 8s. Some see points, too, but they’re not as interesting. (There’s a list here.)
If the Earth’s orbit were a perfect circle, and the Earth always moved at the same speed around the Sun, our analemma would simply be a line**, and the Sun would simply move along that line, reaching one end on the Summer Solstice and the other end on the Winter Solstice. But, no planet’s orbit is a perfect circle.
Remember, if you can, Kepler’s second law for planetary motion.
A line joining a planet and the sun sweeps out equal areas during equal intervals of time.
In other words, when a planet (with an elliptical orbit) is closest to the Sun (perihelion), it moves fastest. When a planet is farthest from the Sun (aphelion), it moves more slowly.
What this means is that the Earth moves different amounts through the sky as it rotates, which is important. You see, the amount of time it takes the Earth to rotate once is not 24 hours. It actually takes 23 hours, 56 minutes, and 4 seconds. Why are our days 24 hours, then? Because, on average, the Earth revolving around the Sun adds an extra 3 minutes and 56 seconds to each day. But during some days (like in March), it appears that the Sun is moving more slowly, so that 24 hours later — what we record as a day — the Sun has shifted its position in the sky.
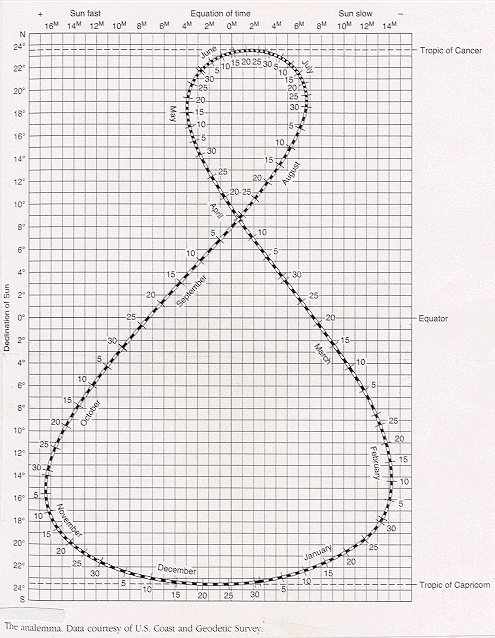
This difference between the Mean Solar Time, which is our 24 hour day, and the Apparent Solar Time, which is how long it takes for the Sun to return to its same position in the sky, governs this “side-to-side” motion in the analemma. The math is given by the equation of time. But, intuitively, how does this work?
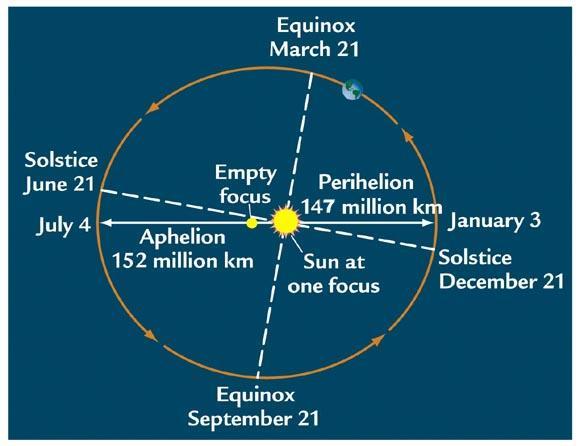
It turns out that aphelion and perihelion are close to the solstices on Earth. During these times, a day is actually very close to 24 hours. When the Earth moves from aphelion toward perihelion (when we’re experiencing the autumnal equinox in the Northern hemisphere), the Sun appears to move quickly, and so it reaches its apex in the sky at times slightly earlier than during the solstices. Conversely, when the Earth moves from perihelion to aphelion (during the months of February and March, for example), the Sun appears to move more slowly, and so reaches its apex at slightly later times than normal.
We call these two situations a “fast Sun” and a “slow Sun”. If the y-axis of the analemma was due to the Earth’s axial tilt, then the x-axis comes from the Sun appearing fast or slow:
So why is Earth a figure 8 and Mars a teardrop? Because Mars’ perihelion and aphelion line up close to Mars’ equinoxes, rather than the solstices like it does on Earth. Know what this means? As the Earth’s equinoxes precess (which they do over a time period of 26,000 years), the shape of our analemma will change. So enjoy the figure 8 now, while we have it!
Update: An astute commenter has pointed out that the Earth’s axial tilt also contributes to the Sun’s apparent motion in not just the up-down direction, but also in the “side-to-side” motion. I’ve managed to find an animated image that shows:
- the effect of eccentricity (what I talked about above),
- the effect of axial tilt (something that most planets have),
- the combined effects of both of these (which gives us our equation of time), and
- the overall path of the analemma, which aligns neatly with the equation of time.
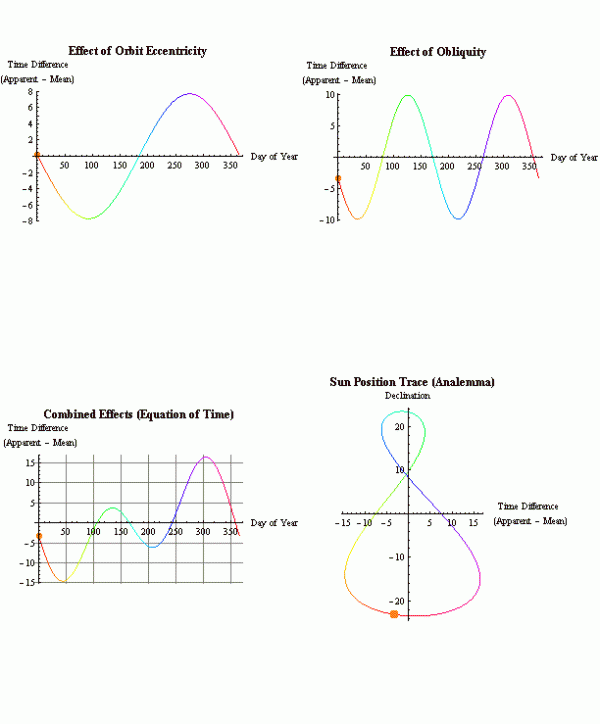
So, if one of these (like eccentricity) always dominates the other (as is the case on Mars), we get a teardrop. If one of them (like eccentricity) is significant and the other is practically zero (as is the case on Jupiter, with a 3 degree tilt only), you get something much closer to an ellipse. And if both are important enough that sometimes eccentricity dominates and sometimes axial tilt dominates (as is the case for Earth, with a tiny eccentricity, and Uranus, with a huge 88 degree axial tilt), you get a figure 8!
** — Also, note that what I wrote up top about the analemma simply moving up and down in a straight line is also incorrect. The Earth’s axial tilt (also called obliquity) would still be present, and would still contribute to the side-to-side motion of the Sun in the sky, even if the orbit were a perfect circle.
So you see, this deceptively simple question is actually incredibly complex, and I make mistakes sometimes!
August 26, 2009
August 26, 2009
August 26, 2009
August 26, 2009
August 26, 2009
August 26, 2009
August 26, 2009
August 26, 2009
August 27, 2009
August 28, 2009
August 28, 2009
August 28, 2009
September 8, 2009
November 1, 2009
January 20, 2010
June 10, 2010
April 28, 2011
March 29, 2012
June 14, 2013
