Striving for the Speed of Light

Posted by Ethan on June 1, 2011
(53)
More »

“The very closest stars would require many years to visit, even traveling at the speed of light, which is impossible according to Einstein’s theory of relativity. Today’s fastest spaceships would require 200,000 years to travel to Alpha Centauri, our closest bright star. The energy required to send a hundred colonists to another star, as Frank Drake has pointed out, would be enough to meet the energy needs of the entire United States over a human lifetime. And these estimates are regarding nearby stars. When we consider the distances across the entire galaxy, and between galaxies, interstellar travel seems absolutely untenable.” -David E. Fisher

It’s always easy to point out the difficulties with a dream. The stars, after all, are so incredibly far away, that the distances are, well, astronomical.

Image credit: Roger Groom.

Alpha Centauri, the closest bright star (the bright, yellow one, above) to us, is about 270,000 times farther away than the Sun is. And the farthest a human has ever traveled, of course, is to the far side of the Moon, just 0.4% of the distance to the Sun.

That, of course, was something that we did back during the Apollo missions. And there was a very impressive thing that happened. Back during the 1960s and 1970s, we launched human beings into space, for the first time, with sustained accelerations for record-breaking periods of time.

Image credit: Ctein.

The Saturn V rocket — shown here during the 1972 launch of Apollo 17 — was capable of accelerating humans from rest to a speed of 25,000 miles-per-hour (about 11 km/s), over the timespan of only about 10-15 minutes.

We’ve done it hundreds of times in the United States alone, as the space shuttle now does almost exactly the same thing.

The key, of course, isn’t to get as large of an acceleration as possible. Here on Earth’s surface, we are accelerated towards the Earth’s center at a constant rate of 9.8 m/s2. That’s the force of gravity that pulls us (and everything else) down.

But if we built a device — theoretically — that could accelerate us at that rate for an arbitrarily long amount of time, could we ever reach the speed of light?

Look, Your Worshipfulness, let’s get one thing straight. I take orders from just one person: me Einstein.

You might think that all you have to do is take that acceleration and sustain it, and you’ll eventually reach the speed of light. Let’s take a look at what happens if you could do it!

At first, you’d notice that you’d just be going faster and faster, just like you wanted. You’d need to apply a constant force to your ship, and as long as you did, you’d keep on increasing your speed. The graph above looks like a nice straight line, and as the seconds turned into minutes, and the minutes turned into hours, you’d find yourself speeding up, faster and faster, gaining an extra 9.8 m/s of speed for every second you continued to accelerate. The human speed record, at 11 km/s, would be passed in under 20 minutes.

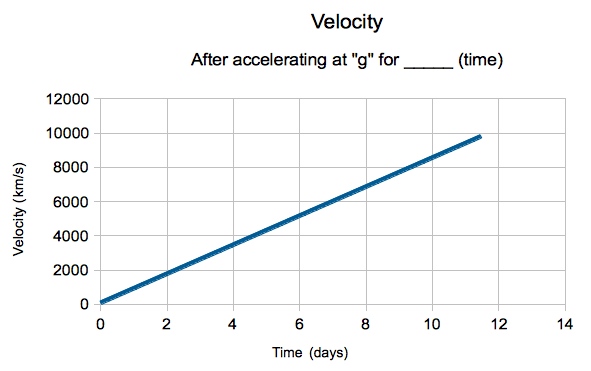
And as the hours turned into days and eventually weeks, you’d think you were headed on your way to the speed of light. At exactly 299,792.458 km/s, you might look back sometime after a little under three-and-a-half days, and mark the milestone that you were 1% of the way there. And perhaps you’d get giddy, after almost a full week, when you realized you were 2% of the way to the speed of light. After all, at 4.37 light years away, Alpha Centauri doesn’t seem so distant if you can make the trip at the speed of light!

But as the weeks passed by and turned into months, you would notice something very interesting, if not troubling.

Even with the same force and the same thrust, you wouldn’t be accelerating quite as quickly as you were at the beginning. This is very bizarre and counterintuitive, and is a consequence of special relativity. It gets harder and harder to change your speed as you start to get close to the speed of light. But if the curve in the above graph isn’t enough to tip you off to the trouble you’ll encounter trying to get up to the speed of light, perhaps you’ll really be able to see what’s going on if we start looking at this sped-up spacecraft after a few years of traveling.

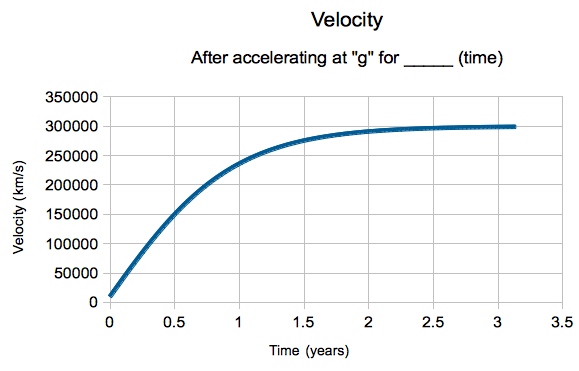
There’s a limit to how fast you can go! And while you can’t quite tell from the graph, you don’t reach the speed of light, you just approach it.

Even in the graph above, you continue to accelerate the whole time, and approach the speed of light, incrementally. After about 15 months, you’ll have attained 90% the speed of light, which is truly amazing, but not what you would have naïvely expected if you had simply continued your original “straight line” graph of velocity vs. time.

And after about two-and-a-half years, you would reach 99% the speed of light. But will you ever get there? Let’s extend the journey for a whole decade and see.

From this graph, it’s impossible to tell. But if I look at the difference of the speed of light (c) and your speed (v), what I’ll call c – v, perhaps we can tell.

After all, it took about a year-and-a-quarter to reach 90% of c, and about 2.5 years to reach 99% of c. Will this pattern continue? A graph of c – v won’t show that, but a graph of the log of c – v will!

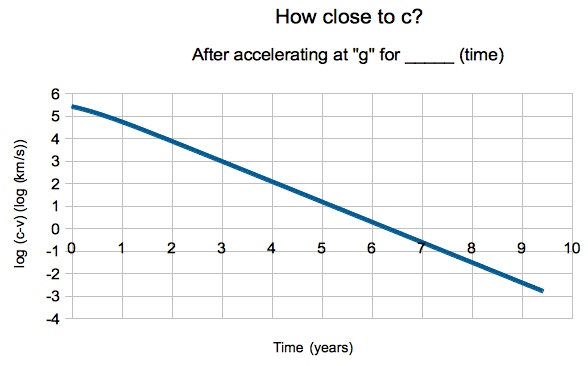
(For those of you aspiring to become scientists, teaching computers to do your calculations/graphs/dirty work is a must!)

A difference of 1 in the log means a factor of 10. So after about 4.5 years, we’re up to 99.99% the speed of light. By time about 6 years and 4 months have passed, you’re moving at 299,791 km/s, just one km/s below the speed of light. But — while the first km/s took only 102 seconds to attain — this last one never comes. After another year, you’ve made it another 0.9 km/s, and after another 3 years, another 0.999 km/s.

So you can continue to approach the speed of light, spending an incredible amount on fuel and thrust, but you’ll never get there.

And, of course, there’s the one thing we haven’t talked about, which is the true cost of this.

All of this was calculated assuming a constant thrust, or force-per-unit-time. Which is a fine assumption. After all, that’s about what the three-stage rocket that launched the Apollo astronauts achieved.

But the big cost comes in terms of energy. The first ten minutes of acceleration takes a certain amount of energy, and by the end of it, you’re moving at about 6 km/s. The second ten minutes, however, will get you up to double the speed at 12 km/s, but takes three times as much energy. The next ten minutes will get you up to 18 km/s, but uses up five times as much energy as the first ten minutes.

And this pattern continues. By time a year has gone by, you’re using over 100,000 times the amount of energy you started out using, and you’re still using it every ten minutes! Not only that, but you’re not even increasing your velocity by the same amount; your attempts to change your speed get progressively less and less effective.

Image credit: Steve Bowers.

Which isn’t to say that we should give up on interstellar travel! It simply helps us be aware of what the obstacles are that we’re trying to overcome, so that we can figure out how we might do it.

And remember, this is space, where there’s no air, so once you reach your desired speed, you can simply coast at that high velocity until you need to slow yourself down. (And that, of course, takes the same amount of energy it took to speed yourself up!)

The most fun part about this, for me, is that if you work out how time dilation and length contraction work, you can literally — given as much energy as you want — reach any star or galaxy within about 13 billion light years of us in just one human lifetime. That’s the cost and reward of reaching for the stars, and it’s the limit of the speed of light that allows us to understand exactly what it takes to make it happen!

(53)
More »

Comments

  1. #1 Lou Jost
    June 1, 2011

    Do you remember Freeman Dyson’s ORION project? He worked out a system for maintaining the acceleration without using up all the rocket fuel on the planet. His plan was to dump atomic bombs out the back of the rocket and detonate them, pushing the rocket forward. This would eventually accelerate the rocket to near c using “reasonable” amounts of material. These rockets would have to be huge, but your observation about our exploration radius would apply to them—perhaps we really could explore the universe, if we wanted to! This also means that non-earthly species could do the same…

  2. #2 D. C. Sessions
    June 1, 2011

    And remember, this is space, where there’s no air, so once you reach your desired speed, you can simply coast at that high velocity until you need to slow yourself down. (And that, of course, takes the same amount of energy it took to speed yourself up!)

    Well, there isn’t much out there. Then again, at useful speeds you don’t need much. At one hydrogen atom per cubic meter (which is more like intergalactic than interstellar density) you’re still running into a turning an awful lot of kinetic energy into hard radiation by the time you crack 100 km/s.

    Which not only slows you down but, over the course of a few thousand years of travel, fries damn near every bit aboard.

  4. #4 Electronics Recycling
    June 1, 2011

    it’s both good to see that we have such a solid grasp on the difficulties of interstellar travel, and saddening to realize that it will probably not occur within my or my children’s lifetimes.

  5. #5 Pete
    June 1, 2011

    Great post Ethan! I simply never get tired of hearing about space travel. If I don’t get to ride on a spaceship in my lifetime, I’ll consider my life a failure (I’ve been convinced of this since the age of about 5).

    Will you be following this up with a focus on the relativistic effects? Even though Alpha Centauri is over 4 light years away, say you traveled at over 90% the speed of light for over half the trip (big assumptions I know), that would cut down the travel time quite a bit (90% c = 1/2 time flow approx I think). So that would take the travel time down to maybe 3 years… Hmm… did you already do a post on relativistic effects? I think you maybe have…

    I really do believe we will see spaceships capable of interstellar travel within our lifetimes. Although to believe in that you also have to believe our lifetimes are going to be extended quite a bit, but a belief upon a belief is fine by me if it means I can hope to be Kirk. Which is really the main reason anybody is involved in science aren’t they? Spaceships and green alien girls?

    Kirk in action:
    http://www.youtube.com/watch?v=IZU9u2cTiS8&feature=player_embedded

    (sorry for the rambling post, early in the morning here and excited about spaceships)

  6. #6 Mark M
    June 1, 2011

    100-yr round trips won’t bother us if we conquer the aging process.

    Technological immortality is just as good as warp drive. And more feasible.

  7. #7 Schenck
    June 1, 2011

    Great post, love these explanations you’ve been putting out, keep it up!

    You say at hypothetical best we could blast 13 billion light years away over the course of our lifetimes. In an earlier post you noted that the visible Universe is around 46 billion light years in diameter. So if you blasted off in your rocketship at full speed, your grandson would (more or less) would be the captain by the time the ship was outside of that diameter no? The Vis. Uni. would be expanding alongwith it, but eventually you’d surpass it no, and slowly be redshifting out of the visible spectrum?

  8. #8 D. C. Sessions
    June 1, 2011

    100-yr round trips won’t bother us if we conquer the aging process.

    That depends on how much hard radiation damage that anti-aging treatment cures. One hopes it’s enough to let you keep repairing all of the electronics on board, because they’ll be toast.

  9. #9 Phil
    June 1, 2011

    I love your blog ethan, it’s been smack in the middle of my opera speeddial for ages. It makes me regret I studied a language and not physics ;-)

    Anyway. I have a little question, I’m pretty sure what the answer will be, but nonetheless, here it goes.

    In mathematics, 0.9999999… = 1

    So if you would spend eternity accelerating your spaceship, you’d reach 99,9999999999999….% of the speed of light, right? Wouldn’t your speed at some point basically become the speed of light? I mean, you’ll be so close that there’s pretty much no difference anymore. Or would physics really behave so much different between 100% and 9,9999~%?

  10. #10 Keith Harwood
    June 1, 2011

    If you can accelerate at one g for a year or so it’s easy to go faster than light. How? You cheat. You measure the distance travelled on a map you picked up at your starting point and you measure the time taken on the clock you carry with you. Just don’t go outside and actually mesure your speed.

  11. #11 Randy Owens
    June 1, 2011

    Well, time for me to pick at a couple of nits again. Firstly, the more clear-cut one:

    At exactly 299,792.458 km/s, you might look back sometime after a little under three-and-a-half days, and mark the milestone that you were 1% of the way there.

    Unless I’m misinterpreting the “looking back”, you mean when you’re actually going .01c? If so, then 2,997.92458 km/s; what you have there is 1c itself.

    Secondly, aren’t you mixing up reference frames here? You keep referring to time as it passes for you on the ship, but as far as I can tell without fully working out the calculations, it looks like those graphs are for time measured from a stationary observer. Which is fine, as long as it’s made clear that that’s whose time is on the X-axis.
    But I was always more interested in what happens for the time of the person on the ship, anyway.

  12. #12 Roland
    June 2, 2011

    But once you build up some speed, impact with any old BB of a rock can take you out in a blaze of something-or-other. And any incoming radiation (from head-on) will be boosted way above gamma ray frequencies, penetrate the ship, and fry you. Nice try, though.

  13. #13 Richard Meyerson
    June 2, 2011

    Unless my meager understanding of G.R. is lamer than my understanding of women, I believe that, should one actually approach the speed of light and able to traverse the visible universe in roughly 13 billion years while aging only several years oneself, taking photos of the various alien species he encounters, then returning home, aging only a few more years only to find that the earth was swallowed up by an exploding sun many billions of earth years ago. Such is the nasty effect of time dilation.

  14. #14 Waydude
    June 2, 2011

    I thought Proxima Centauri was our closest neighbor star?

  15. #15 Randy Owens
    June 2, 2011

    @Waydude: He does consistently say “closest bright star” about Alpha Centauri. Despite being slightly closer than the rest of the system (assuming Alpha is a system), Proxima isn’t too bright–apparent magnitude about 11, and so dim it wasn’t even noticed until 1915.

  16. #16 Alan L
    June 2, 2011

    It’s a shame that science has decided that a fourth spatial dimension cannot possibly exist.

    If it did exist then whatever velocity a space ship attained in three space should square the moment it entered four space, assuming integration of the formula: v = s/t is valid in this hypothetical situation.

  17. #17 Alan
    June 2, 2011

    An often overlooked limit on intersteller travel is the fact that even on Earth we don’t know how to build a biodome that can last more than about a year. This includes not only food and water but also a breathable atmosphere.

  18. #18 Chris
    June 2, 2011

    Great post and great blog.

    I’d love to see an article here giving an example of the time dilation equations in action. I’m sure you (the writer of this blog) could have some fun with that and make it pretty interesting.

  19. #19 Peter
    June 2, 2011

    sigfpe had a nice article about this topic as well, you can read it here: http://blog.sigfpe.com/2009_04_01_archive.html

  20. #20 dean
    June 2, 2011

    Neat article. I must be a bit odd, however, because the thing that jumped out at me as a “holy s**t” point was this:

    The energy required to send a hundred colonists to another star, as Frank Drake has pointed out, would be enough to meet the energy needs of the entire United States over a human lifetime.

    I’m still boggled by this.

  21. #21 Tappancs
    June 2, 2011

    I’ve always thought you could look at relativistic effects in the following way: all objects in the universe are moving at the speed of light in 4-dimensional space-time. When we are at rest (spatially), we are moving at the maximum speed through time. The faster we move through space, the slower we travel through time.

    I know it’s probably a bit of a silly way to look at it, and of course it doesn’t cover the time dilation effect you get from gravitation, but I thought it was an interesting way to picture it.

  22. #22 grey eminence
    June 2, 2011

    superluminal propulsion [faster than light speed]

    anti-matter near light propulsion

    light speed propulsion

    anti-gravity

    These are things that already have a physics solution.

    http://colossalstorage.net

  23. #23 Neil
    June 2, 2011

    What’s really boggling is the number of “serious” proposals I’ve seen that ignore the energy cost. Drake was making some pretty optimistic assumptions to come up with an energy requirement that low. Firstly it requires a top speed of 0.1C, so the trip takes 50 years. Then the mass of propellant and fuel must be low compared with the payload. And of course we need an extremely efficient method of converting energy to thrust. Using existing technology, or even plausible extensions to it, would require vastly more than a lifetimes worth of the world’s energy consumption.

  24. #24 Vicki
    June 2, 2011

    The thing about “you could do it in a lifetime” is that, at minimum, it’s permanent exile from everyone you know who isn’t on the ship with you. Ursula Le Guin wrote a story (“Vaster than Empires and More Slow”) about an exploration ship all of whose crew members were mentally ill, because no sane people volunteer for a trip that would take them away from their homes for 300 years.

    This is also going to make it hard to get funding: who is going to pay for an expedition that won’t be sending results back until all the funders are long dead?

  25. #25 OKThen
    June 2, 2011

    And that is how it is!!
    (except for the nit which Randy Owen pointed out)

    Yes, to all of the dangers and challenges about interstellar space travel at near light speed. But problems can be solved. e.g. consider energy requirement.

    In 2008, the world consumed 474 x 10^18 joules of energy.
    ____!!! Since, E = Mc^2;
    One 5 lb. bowling ball contains 4.5 x 10^17 joules of energy; 1000 powers the world.

    Of course, there will be inefficiencies converting mass to energy even with best future technology; so let’s assume we need the mass of 1 million bowling balls.

    But we just need a spaceship to carry enough mass to get started; we can collect the rest as interstellar dust along the way. And as we approach the speed of light, the mass of a typical speck of dust will relativisticaly contain much more mass; and thus mass to energy conversion will supply our spaceship with an increasing amount of energy as the velocity of our spaceship increases.

    So we just need to learn to harness the interstellar dust to give us energy; rather than let those massive specks of dust destroy our spaceship.

    Thus amount of energy is not a problem; enough energy is everywhere. Learning to safely harness energy is the challenge. The easy step is learning to unsafely harness energy(e.g. a bomb); the hard step is learning to safely harness energy (e.g. a power plant).

    First we learn to safely harness nuclear fusion; then we learn to harness dust.

  26. #26 Roger
    June 2, 2011

    Subluminal Warp Drive powered by aneutronic fusion can be possible soon.
    http://www.youtube.com/watch?v=sgAwyr5Udzw

  27. #27 Ben P
    June 2, 2011

    The thing about “you could do it in a lifetime” is that, at minimum, it’s permanent exile from everyone you know who isn’t on the ship with you. Ursula Le Guin wrote a story (“Vaster than Empires and More Slow”) about an exploration ship all of whose crew members were mentally ill, because no sane people volunteer for a trip that would take them away from their homes for 300 years.

    If we’re getting into relativistic time dilation I’d also recommend The Forever War by Joe Haldemann and the Ender Series by Orson Scott Card.

    Both envision a future universe where humans have mastered space travel at high %c speeds, but time dilation basically ensures that spaceflight is a one way trip for everyone you knew back on earth, because by the time you reach your destination, you’ll have aged a month or two, and the people who left behind will be old or long dead.

  28. #28 Glen Martin
    June 2, 2011

    Another thing to consider: Halfway to one’s destination, it would be necessary to turn the ship around and begin a 1g deceleration. After all, it wouldn’t do much good to arrive at the destination system travelling at a substantial portion of c.

  29. #29 intercostal
    June 2, 2011

    I don’t think the “permanent exile” bit is all that problematic; going to the New World, for most people, was pretty close in the 17th and 18th centuries (unless you were a governor or really, really rich).

    Anyway, given the world population, only a tiny percentage of people need to be willing to go.

    —

    Biodomes: I’m not convinced it’s quite as hard a problem as all that. “Biosphere II” was not well designed, IMO: it was too complex a system, and too built to imitate Earth. It’ll take a lot of experimentation, but it’s going to be a much easier problem than the energy levels/propulsion needed — by the time we have that, I think biodomes will be a thoroughly solved problem.

  30. #30 James Fuller
    June 2, 2011

    All such heavy breathing about mass and acceleration and velocity will be obviated when the solution appears, namely the way to get from here to there without slogging across the intervening distance.

  31. #31 Darren Garrison
    June 2, 2011

    There are on-line applets that allow you to calculate the parameters of fast interstellar flight and determine things like travel time and relativistic mass. Here’s one of them:

    http://orimath.com/oritutorial/RelCalc01.html

  32. #32 tjaracas
    June 2, 2011

    I believe that everything can be build as long as it is economically feasible. It just takes time, knowledge and interest. Last factor an important item that not should be overlooked. Why build interstellar travelling capable spaceships if we gain nothing out of it? Maybe the Webb telescope, whenever launched, could pinpoint to really useful destinations.With the Alpha Centauri system we just know that at this moment Proxima Centauri is the closest Star to our Earth. We still don’t know if the system has planets and we don’t know what we should do when we are close to the system. With the Kepler data we already have a bunch of interesting objects and after the current data will be confirmed we have a lot of habitable multi planet solar systems to discover that we at least can colonise. For humans the biggest danger outside our atmosphere to overcome is harmful radiation. I am a firm believer that interstellar space travel will be made possible, maybe on a nano scale, in my lifetime-.

  33. #33 JK Finn
    June 2, 2011

    @Alan L #16:

    It’s a shame that science has decided that a fourth spatial dimension cannot possibly exist.

    Funny, I’m personally more worried about the three other ones…

    To be a bit more serious, is there actually any physical or theoretical reason to assume that the emergent macroscopical 4-D structure of spacetime is a manifold at all?
    Another approach would probably support @James Fuller #30.
    NB: This may come through as a double comment, I keep getting a “too many connections’ error here even in preview.

  34. #34 Jesse
    June 2, 2011

    I remember one proposal for the “warp bubble” – the Alcubierre idea. I was curious as to whatever happened to that? As I understood it the issue there was warping local space took more energy than there was in the universe.

  35. #35 ToSeek
    June 2, 2011

    I suppose the Saturn V was capable of accelerating the Apollo spacecraft to escape velocity inside of 15 minutes, but that’s not actually what happened. It was first launched into Earth orbit and then only after an orbit or so to make sure all systems were go was the third stage reignited to send the astronauts to the Moon.

  36. #36 Vicki
    June 2, 2011

    I love the arguments that basically say “It will be solved once it’s solved.” Tjaracas is saying “anything can be built if it’s economically feasible,” which ignores that physics strongly affects what is economically feasible. In particular, if something isn’t physically possible, you can throw money at it forever without it happening. And James Fuller is handwaving away the entire problem by assuming that we can travel not merely faster than light, but at infinite speed (large distance divided by zero elapsed time = infinite velocity). Why not just handwave up a few more habitable planets right here in our Solar System? (The physics pf that is probably less problematic.)

    By contrast, OKThen is being modest, by only assuming safe controlled fusion power that can be transported in a small space. (A star 150 million km away may be safe fusion power, but it’s not controlled or transportable.)

  37. #37 James Fuller
    June 2, 2011

    > Why not just handwave up a few more habitable planets
    > right here in our Solar System? (The physics pf that
    > is probably less problematic.)

    Hey, that’s the implementers’ problem. I’m just the concept guy.

  38. #38 Frank Lipsky Scottsdale,AZ
    June 2, 2011

    In simple english;given current scientific knowledge;humans can never leave our solar system even if we had the money!
    The limiting speed of light and energy costs
    are fundamental limits;unless new physical laws are discovered .The ‘mental masturbation” of men/women in deep space is promoted by NASA and the Space industry.worse it diverts attention to the fact that our lives will be on this planet and nowhere else;i.e. conserve resources that can’t be replaced

  39. #39 Sarah Scoles
    June 2, 2011

    I think it’s a really scientifically responsible thing to do to first point out the logical, technological difficulties with a ‘dream’ and then address the benefits of overcoming those difficulties, rather than throwing up our hands and saying, “No way! Impossible!”

    Also, here’s a response to all those people in tenth grade who said that asymptotes had no real-world applications.

  40. #40 Matthew Bright
    June 2, 2011

    No matter how much you put into it, not matter how cheap gas is, you’ll never have enough money to reach the speed of light.

  41. #41 Alan L
    June 2, 2011

    @JK Finn 33.

    I tend to lean towards Lisa Randall’s concepts. regarding higher spatial dimensions.

    Who knows, perhaps Invisble DM might be the source of universal gravitation itself. IDM sure as hell is a major player in the whole gravitational problem.

    This would have no effect on GR in any way; Einstein’s own comments on space time were that:

    “Space-time does not claim existence in its own right, but only as a structural quality of the [gravitational] field.”

    and

    “Space and time are modes in which we think, not conditions in which we exist.”

    So he never claimed to have explained gravity any more than Newton did.

  42. #42 Christine
    June 2, 2011

    I love to read about science and technology because there is still so much that is unknown, leaving room to dream of all the possibilities. Reading this article which strives to create a way to travel through space at what we know of as the current maximum speed of travel, light. All of the articles I have read (which really isn’t too many) that explore different possible therories on space travel the methods all use a model with the vehicle being propelled forward at an extreme rate by force, just as vehicles on earth are created to travel. Which brings my thoughts to dream of other possibilities and creates a few questions that challenge the currently known. It is assumed that in space a black hole is a gravitational pull so strong that it even consumes light. Going on this theory I wonder if the laws of physics could be altered or changed in Space when it comes to travel due to the difference of the enviornment and how it may change as travel threw space itself. The solar systems are held together in a balance of gravitational pulls, but I would think not all are balanced with the exact amount of force or there would be no existence of the possibility of a black hole. Am I wrong in my theory? I also am under the impression that temperature can impact the the rate of how fast matter (or spaceships) are able to travel. So I am left to wonder with all the unknowns that science is finding answers for if there is any possible way to create a vehicle that travels through space in a manner that is pulled (like a vacucum) instead of pushed using the natural gravitational pulls through space could find a special “Space Law of Physics” that would allow the speed travel to exceed the speed of light by traveling in a manner that would mimic the pull of a Black Hole?

  43. #43 greame
    June 3, 2011

    @24 “no sane people volunteer for a trip that would take them away from their homes for 300 years”

    Call me mentally ill, then.

  44. #44 Gammaburst
    June 3, 2011

    If we spent the first half of the trip accelerating at g and the second half of the journey decelerating at negative g then wouldn’t the time dilation effects cancel out?

  45. #45 Vicki
    June 3, 2011

    Gammaburst–

    The time dilation effects don’t cancel out because time dilation comes from velocity, not acceleration, and we’d be spending significant parts of the trip traveling at relativistic velocities.

  46. #46 Samantha Vimes
    June 3, 2011

    Why would no sane people go? If you don’t have family, your family is your friends. If you’re in an intense career like being an astronaut, most of your friends are your co-workers. For a long journey in a spaceship big enough to have a hydrogen scoop sort of propulsion system, you’d be sending a big crew.
    It would be one fuckin’ rad road trip with your besties. You don’t have to be antisocial or imbalanced to want to do that– you just have to not be in a position to worry about missing the birth of your grandkids. In fact, some of the older astronauts might even be able to make a family thing of it– 51 & 54 year old astronaut and physicist parents with doing-a-PhD-project-in-space-colonization kid who’s dating radio-specialist-amazing-intern. I’d envy them.

  47. #47 David H. Eisenberg
    June 5, 2011

    What a hysterical article. When we discovered time travel and faster than speed of light travel at the same time in 2062 (I can’t take any credit – I was 3 at the time), it revolutionized everything, of course. But, it took another world war (you thought II was bad – just wait kids), and then two different one world governments (which people thought they wanted, until they realized it just meant an all powerful tyranny) before time travel was given to the masses and governing became not only impossible, but unnecessary. Not surprising, it turned out that there were no aliens even remotely like us in the universe and that any we met either tried to eat us or were oblivious to our attempts to communicate. The most intelligent life form we discovered up until I came back here, was shaped like Broccoli and have all the mental capacity of kangaroos (aka, in my time – “Australian road kill). But, some of us who stayed on earth and just t-traveled found that even time machines can be defective, and given enough travel, inevitably malfunction. If you went back in time, and your power pack dies (for reasons you wouldn’t understand, you can’t take an extra one with you or kaboom), it is impossible to replace it until t-travel is invented (or re-invented, depending on your perspective). Go back too far, and you won’t live long enough to get “home” again, even though we live quite a bit longer than we used to thanks to fetal dna manipulation. The first irony is, if you do live long enough and you get “home,” you just have to go through it all over again, and get stuck in the past again, because the whole “the future isn’t fixed” idea turns out to just be an incorrect movie plotline and time loops turn out to be exactly what happens. That’s an immutable law of nature as far as we can tell. So, this is my third time around going back to 1959. The second irony is that no matter how often you prove you are from the future, no one really believes you, at least not for long. Depending what time period you are in, they think you are a witch, or a charlatan or even just lucky. That’s just human nature. So, after your second go round, you stop trying or just enjoy yourself with it like I’m doing now. The third irony is that so much of what scientists are sure of these days, is not only wrong, but humorously so. In my time, Einstein is known as “the unkempt idiot,” and we know there is really no such things as dark matter, dark energy or “eating right” (we all laugh about that one).

    And, just in case you are wondering, yes, I do know who is going to win the Super Bowl next year. But, if I told you, you wouldn’t believe me. You certainly didn’t the last two times and I’m done trying.

  48. #48 John Weck
    June 6, 2011

    Traveling to the stars and biology are not very compatible. There is no reason to think about human limitations at all when discussing interstellar exploration and culture. Homo sapians are not going to make colony ships, throttle their way to the stars, or hoe alien loam to grow crops. Limited biologicals are staying behind back at sol, and only hardened computers are going to make it to the stars, and survive. Star travel doesn’t require collosal amounts of mass to cart around biological forms, and human lifetimes are irrelevant.

    Our minds are really computational in nature, and that’s what needs to go to the stars. The nice thing about computers is that they can hold a virtual world and a set of minds to inhabit them. That means that you can explore galaxy with minimum energy usage, and even teleport anywhere in a interstellar communications network instantly (subjectively) if you like. Of course the data-link still travels at the speed of light, but you won’t notice that, just the cultural differences when you arrive.

  49. #49 idealist707
    June 6, 2011

    I seem to remember a link from some years ago, leading to a presentation of a theory which made light speed possible. It won the award for some USD 200.000 from the DOD. The idea simply was the reduction, temporarily, of mass.
    Anybody got that link?
    BTW, getting older means everything in the past gets further and further away.

  50. #50 James Ph. Kotsybar
    August 23, 2011

    OFF THE SCALE
    — James Ph. Kotsybar

    The young lady known simply as Bright,
    who could travel at speeds fast as light,
    said. “While I’m never late,
    I’m concerned that my weight
    goes to infinite mass, though I’m sleight.”

  51. #51 Bob Bryan
    New Jersey
    July 29, 2012

    You are forgetting about Einsteen’s Theory of Relatively.

    Joe Einsteen of Hoboken, NJ came up with a theory that science fiction that worries about Relativity is Relatively boring.

    Actually this is from the Robotman comic strip from several years ago but it seems relevant.

  52. #52 Lighthouse Dev LLC
    Maryland USA
    December 14, 2012

    Great Post.

    If one could build self replicating H bomb factory on the moon. Then a multi-stage Orion the approaches speed of light might be possible. Which would also be a time ship. If the very rich is willing to pay a billion dollars for a trip to the moon, then how much could one get for a trip to 100 years to the future.

    Cheers,
    Bert
    –LINKS REMOVED–

  53. #53 Lighthouse Dev LLC
    Maryland USA
    December 16, 2012

    Instead of using a billion nuclear bombs, a small black hole could power a star ship to near the speed of light. Of course building the first micro black hole is the trick/

    http://io9.com/5391989/a-black-hole-engine-that-could-power-spaceships