Dark Energy, Accelerated Expansion, and Energy Conservation: Does it all make sense?

Posted by Ethan on December 2, 2011
(48)
More »

“I have long held an opinion… that the various forms under which the forces of matter are made manifest have one common origin; or, in other words, are so directly related and mutually dependent, that they are convertible, as it were, one into another, and possess equivalents of power in their action.” -Michael Faraday

For centuries, the idea that you can’t get something for nothing was floating around long before we knew about the most important conservation law in all of the Universe: the Conservation of Energy.

Image credit: Mr. Torgerson's 6th grade class.

For example, the ball rolling down this hill, picking up speed and gaining kinetic energy isn’t getting that energy from nothing! It’s actually turning a different form of energy — gravitational potential energy — into that kinetic energy. And, at any point along its journey, the total amount of energy — its kinetic + potential energies — is the same.

As long as you consider a closed system, or a system that cannot gain/lose energy from/to someplace outside itself, the law of conservation of energy is perfect.

Image credit: the University of Idaho.

The Earth, for example, is not a closed system on its own. It receives light and energy from all across the Universe, most notably from the Sun, and also radiates energy off into space. The Sun, too, is not closed, as it constantly radiates energy away into space, but its energy isn’t coming from nowhere; it’s being created by converting some of its rest mass energy into light and heat (and neutrinos) via nuclear fusion and E = mc2. When all the input sources and output sources of energy are included, for any system in the Universe, the conservation law holds.

Image credit: Max Camenzind at the University of Heidelberg.

While there are some spooky quantum effects that may seem to violate our intuitions concerning this law, from the smallest subatomic scales to the largest cosmic ones, once all the sources and sinks of energy are accounted for, it still appears to hold.

How, then, do we answer the following question, posed by another astrophysicist:

What is the source of the energy for the accelerating universe?

This is an amazingly deep question, so let’s begin by talking about what it means to live in an accelerating Universe.

Image credit: Adam Reiss, Hubblesite.org, retrieved from jdem.lbl.gov.

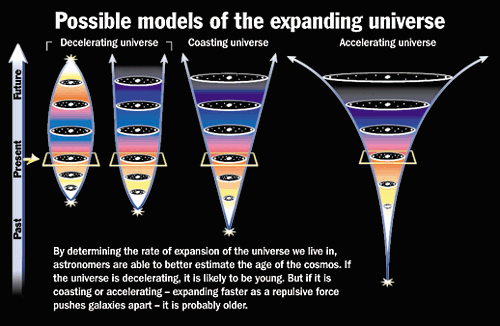
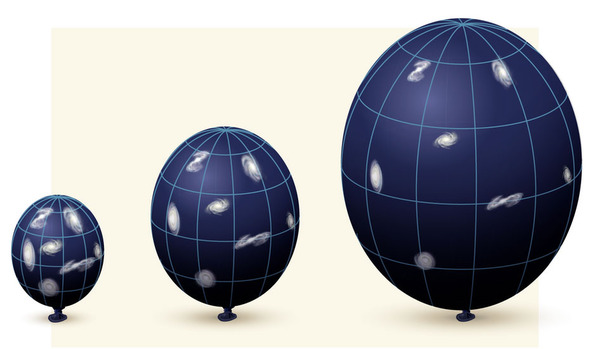
You can imagine the Early Universe — at least the portion of it observable to us — as a hot, dense, rapidly expanding sphere of matter and energy. But you also know that if your Universe is full of matter and energy, the force of gravity is going to do everything it can to try and pull this expanding Universe back together again. So — in the simplest terms you can imagine — that’s what you’ve got: an initially, rapidly expanding Universe, where gravity tries to slow, reverse, and recollapse it.

Looking at the image above, the leftmost diagram represents an expanding Universe where gravity eventually wins: the initial expansion is not enough for the amount of matter-and-energy present, and the Universe eventually reverses its expansion, recollapsing in a Big Crunch. The second image is one with a large initial expansion, but the amount of matter and energy is just one subatomic particle short of being able to recollapse the Universe! In this critical case, the Universe’s expansion rate continues to slow, asymptoting towards zero, but never reverses. And the third case — a low density Universe — continues to expand forever, as the gravitational attraction between all the Universe’s matter and radiation finds itself unable to counteract the initial expansion.

Image credit: Physorg.com / Lawrence Berkeley National Laboratory / BigBOSS.

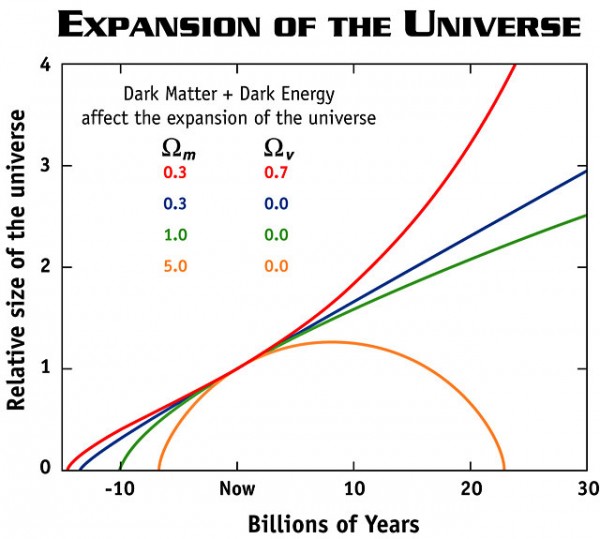
And then there’s the fourth case — the actual case — of an accelerating Universe. This is a Universe filled with dark energy, or a finite, positive amount of vacuum energy intrinsic to space itself. And in this case, the expansion of the Universe doesn’t just “fail to slow down enough” to give us recollapse, but rather distant galaxies moving away from us move away from us faster and faster as time goes on! This means that, if we take a finite sphere of matter and energy to start with, and let it expand over time, the radius of that sphere will increase like so:

Image credit: NASA / Goddard Space Flight Center.

Unlike the recollapsing (orange) case, our Universe will never recollapse. Unlike even the critical (green) or low-density (blue) curves, the “size” of our Universe is increasing at an exponential rate as shown by the red curve. What our best measurements tell us is that the energy density of space itself (i.e., the dark energy density) is neither increasing nor decreasing, but remaining the same.

But this might bother you: if the energy density is staying the same, but space is expanding, doesn’t that violate the conservation of energy? In other words, aren’t we making more and more energy in our Universe over time, and didn’t we learn that energy needs to be conserved?

Image credit: Mark Garlick/SPL, retrieved from BBC Universe.

Technically, we can weasel our way out of this by noting that the big picture I gave you, above, isn’t entirely how it works. Our large-scale Universe is ruled by General Relativity as our theory of gravity. And strictly speaking, energy is not defined in General Relativity, so why worry about conserving it? But there is a very smart way of looking at “energy” that allows us to show, in fact, that energy is conserved even in this seemingly paradoxical situation.

I want you to remember that, in addition to chemical, electrical, thermal, kinetic, and potential energies, among others, there’s also work.

Image credit: Vasily Alexeyev, 1978, retrieved from strengthtech.com.

Work, in physics, is when you apply a force to an object in the same direction as the distance it moves. What this means is that if you apply a force upwards to this upwards moving weight, you do positive work. (I.e., you add energy to the system.) But if you apply a force upwards to a downwards moving object, you do negative work. (I.e., you remove energy from the system.)

This is perhaps clearer if you think about putting your hand underneath a book, and raising and then lowering it.

Images credit: Eric Harpell, retrieved from lpc1.clpccd.cc.ca.us.

When you push in the same direction the book is moving, you do positive work, adding energy to the system, and when you push in the opposite direction, you do negative work.

So now, let’s think of the Universe. You’ve got this sphere-like object expanding, and there you are, this constant energy density (i.e., dark energy) filling the sphere. You’re positive energy. You’re gravitationally pulling this sphere in on itself. But what’s the sphere doing?

Image credit: Eugenio Bianchi, Carlo Rovelli & Rocky Kolb.

It’s expanding. In other words, you’re pulling in the opposite direction as the expansion, and so you’re doing negative work! (Update: So why, then, does the expansion speed up? Sure, dark energy’s positive energy density means that it’s gravitationally attractive to any matter in the Universe, but the magnitude of its negative pressure is what determines the overall rate of expansion!) And so if you’re asking where the energy for this “dark energy” comes from, it comes from the negative work done on the expansion of the Universe!

A little more technically, as Carroll, Press, and Turner stated in 1992,

…the patch does negative work on its surroundings, because it has negative pressure. Assuming the patch expands adiabatically, one may equate this negative work to the increase of mass/energy of the patch. One thereby recovers the correct equation of state for dark energy: P = – ρ c2. So the mathematics is consistent.

Or a little less technically,

“Suck it, monkeys!” -Liz Lemon

And that’s why energy can be conserved, even in a Universe with dark energy!

(48)
More »

Comments

  1. #1 david
    December 2, 2011

    So, dark energy gravitationally pulls this sphere in on itself, but also beacause of GR it accelerates its expansion?

  2. #2 Dark Jaguar
    December 2, 2011

    I’m afraid you’ve lost me there at the last part. At first I’m dark energy but then it seems like you’re saying I’m gravity. I’m not quite sure what to make of it.

  3. #3 Ethan Siegel
    December 2, 2011

    Dark Jaguar @2,

    Dark energy has energy density, just like matter does, but it also has a negative pressure, which is what’s responsible for the accelerated expansion bit of it. GR is pretty profound for allowing this, but the point is that you can deal with it in such a way to contrive a “conserved quantity” with the expansion.

    And if you do that, the thing that gets conserved looks an awful lot like energy.

  4. #4 NewEnglandBob
    December 2, 2011

    This one is over my head. I don’t like the sphere analogy because the universe is not a sphere.

    So what if the DE has negative pressure. That would counteract the expansion for a time, but there is more and more DE. I just don’t understand where it comes from. I love free lunches but this one is 7 courses.

  5. #5 Otto Krog
    December 3, 2011

    My take on dark matter is, that it is a miscalculating, stemming from our presumption that the speed of light is constant.

    What if the speed of light varies through time and space?

    That creates some interesting theory, at least I think so.

    Antimatter is the mind and consciousness of all living entities.

    You are your own universe.

    Reality is where the minds (antimatter) meets the physical universe.

    Interested? Then read my philosophical multiverse theory.

    Google crestroyer theory and find it instantly

    http://crestroyertheory.com/the-theory/

  6. #6 derek
    December 3, 2011

    What, then, is causing the universe to expand? I get that a positive pressure would cause a volume to expand, doing positive work, while a negative pressure (like the “hydrostatic tension” in a drop of water in a capillary tube) would cause a volume to contract, again doing positive work.

    But if dark energy is causing the universe to increase in volume, how is it that it is applying a negative pressure? If something else is causing the universe to expand, what is that something?

  7. #7 Dark Jaguar
    December 3, 2011

    I’m really struggling to wrap my brain around this, but I think I’m missing something fundamental here.

    Why does dark energy make negative pressure that expands the universe when it’s also pulling it in? How does that end up with an expanding universe instead of a deadlocked one? Why doesn’t any other thing that “pulls in” also push out like that?

  8. #8 SCHWAR_A
    December 3, 2011

    What if you think of DE as “lack of gravity”, so, as if gravity in larger distances d does not act with G_0, but with, let’s say G_0*e^(-a*d) and a _very_ small a?

  9. #9 Patrick Dennis
    December 3, 2011

    Ethan, your essays are generally so thorough, but this one sounds as if you received an important phone call just as you were getting warmed up and had to “wrap it” in a couple of sentences.

  10. #10 Peter Fred
    December 3, 2011

    Ethan says:
    “…energy is conserved even in this seemingly paradoxical situation.”

    and Sean says:
    “energy is not conserved in general relativity…”
    Then am I to infer that energy is conserved in Newtonian gravitational theory? Where does the energy come from that supplies the force that attracts the planets? Does it come from the gravitational potential energy?

  11. #11 Ethan Siegel
    December 3, 2011

    Patrick @9,

    What, you mean everyone doesn’t intuitively understand how pressure works on cosmic scales?

    (Just kidding.)

    Thanks for bringing up an excellent point, and I will look forward to taking that topic on next week. Hopefully, this will make a lot more sense in that context.

  12. #12 Chris
    December 3, 2011

    I’ve really tried to understand this, as I’ve always wondered about the ever increasing dark energy in a energy conserved universe, but I lost it in the last couple of paragraphs. I think I’ll read it a few more times to see if it clicks.

  13. #13 Torbjörn Larsson, OM
    December 3, 2011

    I had forgotten about that work balance. In a similar discussion the other week I brought up the adiabatic case. Yay me! =D

    I will certainly refer to this next time the subject comes up. And it will, the social energy to discuss and question cosmology is constant.

    @ Otto Krog:

    The problem is that it is much simpler to assume what we observe (constant vacuum light speed) and have the standard cosmology outcome.

    @ derek:

    If there were no DE and everything else in standard cosmology applied you would have the coasting universe by now (see the figures), or so I understand.

  14. #14 ScentOfViolets
    December 3, 2011

    If negative pressure seems like a hard thing to rap your mind around, consider the ultimate in space opera space propulsion, the reactionless Dirac Drive: take two chunks of mass, one negative, one positive. By Newton’s law of gravitation, they will experience a mutual repulsive force. But while the positive matter chunk will move away from the negative matter chunk by Newton’s first law, the same law says that the negative matter will be repelled towards the positive matter![1] Presto! A reactionless space drive, and one which has no upper bound on it’s velocity parameter.

    Doesn’t this violate the conservation of energy? Similar to the case accelerating cosmic expansion (which is why I brought it up), the answer is no, for here E=1/2mv^2 contributed by the positive mass is balanced by E=1/2(-m)v^2, the kinetic energy of the negative mass. As in the case with negative energy (unsurprisingly), the result sums to zero and there’s nothing to worry about.

    [1]I’ll make a plug for Gamow’s “Thirty Years that Shook Physicists” by saying this is where I first heard this one. A very entertainingly told history of QM and well worth picking up if you haven’t read it already.

  15. #15 Torbjörn Larsson, OM
    December 3, 2011

    Duh! I meant “the social energy to discuss and question cosmology is conserved”, obviously.

  16. #16 Ewan S Fallon
    December 3, 2011

    If I push against a brick wall I have expended work even thought he wall did not move.

    Maybe matter is losing mass and speeds up, or maybe the speed of light speeds up. Anyway why is all this happening so far away in all directions,— are we the center of the universe? Methinks I smell a rat.

    An apparent wind is real to the sail boater, but is different to those on a different tack and doesn’t exist at all for the landlubber.

    If the land lubber is on the “far side” of the universe do we rush away exponentially from him?

    Is a vanishing point in art real only to the person and where they are standing?

    Finally where and what is the source of energy which creates new galaxies all the time and does the exponationallity thingy? What is feeding the singularity being blamed for it and us, and how does it get into all of the multiple imagined universes?

    How about trying “The universe is a disturbed field of pure energy seeking equilibrium” as a reality? A forthcoming book on this is entitled The Dynamic Ether.

    Yeah I know — ether — ha ha ha etc, but just look at the mental gymnastics required by such as the foregoing and still be unable to explain gravity. That is except by bending space around time, or by using gravity to explain gravity; such as the dimple caused by the “weight” of a large body on a rubber sheet somehow stretched and fastened at its ends to god knows what. All this mind you without explaining how this could be in effect on all possible incoming planes of an approaching body or light itself! A dynamic ether does a better job.

  17. #17 Johnfruh
    December 3, 2011

    Would someone, anyone, please, please, define/explain this negative pressure thing to me?
    Just putting a minus sign in front of it does not do it for me. In Physics, pressure is defined as force per unit area/volume. So, in what sense can there be negative pressure? Can the force be negative? If not, then the area or volume must be negative. Neither of which makes any intuitive sense to me. And, please, don’t just tell me that the equations say that pressure can be negative. I know that. I just can’t imagine it. Also, please don’t compare it tension (i.e. pulling rather than pushing). They are not inverses of each other. So, please help this feeble minded enthusiast out if you can.

    Thanks,
    John

  18. #18 spright
    December 3, 2011

    you may not believe this, (i don’t care)
    i looked at electricity as the elusive dark matter, and then things start making sense.
    no dark, black, hidden energy, or massive equations. if they leave out electricity (plasma, electromagnetism) as obvious visible active forces, then the math gets convoluted and imaginary. (singularity anyone?)
    try it. electricity rules
    peace

  19. #19 derek
    December 4, 2011

    There are a few people who are puzzled by negative pressure. I’m not one of those. Negative pressure, or hydrostatic tension, is well known in ordinary physics, it’s just a bit unusual to see in everyday life, because when we pull on things they usually deform in one of the two directions we’re not pulling (Poisson’s ratio), just as when we push, they bulge.

    Pressure is easy to notice, because it’s easier to constrain things so they’ve got nowhere to bulge. But you can hear negative pressure every time you crack your knuckles: your synovial fluid gets trapped in spaces where it’s being pulled in three dimensions, until it snaps. So negative pressure’s not a problem.

    What I don’t get is is an expansion-causing phenomenon that exerts a contracting force.

  20. #20 SCHWAR_A
    December 4, 2011

    @Johnfruh (17):

    Pressure is N/m², which is the same as Nm/m³, energy-density.

    The energy-density is calculated from all masses in our universe based on the usual gravitational law.

    We observe a difference, a “lack” of energy-density.

    Instead of thinking about gravity-law not reaching infinitely far, we conclude that a negative energy-density must exist: DE. It shall diminish the usual gravitational effect.

    Since this _diminishing_ energy-density also is pressure, we say negative pressure…

  21. #21 Duncan Ivry
    December 4, 2011

    “As long as you consider a closed system …”

    There are physical laws starting with the precondition of having a closed system. Is the universe a closed system? Is this an assumption made just because we don’t know better? You know, Occam’s razor and all this. Or can someone give some reasons?

  22. #22 BenHead
    December 4, 2011

    I couldn’t grok this either, even after reading other sources and trying to think about it half a dozen different ways. I think it’s because this is only half the story. This seems like a pretty good post on the topic, although it glosses over many of the details: http://blogs.discovermagazine.com/cosmicvariance/2010/02/22/energy-is-not-conserved/
    Personally, I’d love those details, to the extent they can be explained to someone without a PhD. From Ethan’s post, I can’t see where energy is conserved; it still looks like dark energy, gravitational potential energy, and even kinetic energy all go up and no energy level goes down. That dark energy (really its gravity) is doing negative work and so can extract energy from the system doesn’t do it for me – does that “system” contain infinite untapped energy? (Maybe so, but if such exists, it would seem to make conservation of energy moot anyhow.)

  23. #23 BenHead
    December 4, 2011

    Oh, you linked that blog post yourself. DERP! Still, your alternate explanation raises these questions in my mind. I almost got there with, “If I go up a flight of stairs, then I wouldn’t say that the Earth gained energy by doing negative work, but I could say that the Earth-me gravitational system gained energy that way, and the measured mass-energy of the system would have increased accordingly,” except then I realized that the source of that energy was the chemical energy in my body, and any couldn’t think of a case where energy within the system could continue to do this ad infinitum.

  24. #24 Johnfruh
    December 4, 2011

    @ Derek,
    Thanks for your Hydrostatic tension example. However, I understand that as a pressure difference and I can imagine molecules pulling on each other. In your synovial fluid example, I again see a pressure difference/reduction being caused by the cracking of knuckles. But, a pressure difference is NOT the same as negative pressure. So, sorry, but I still don’t get it. Add to that the concept of negative pressure out in the vacuum of “empty” space. Just what is doing the “pulling”? The example, often given, of a piston being pulled out of an already evacuated cylinder also doesn’t do it for me. Again, what is it that is pulling on the piston? Maybe I’m being too pedantic or maybe I’m just too dense or maybe it is just the terminology. Whatever, the case, I still don’t get it.

    @SCHWAR_A,
    I’m sorry, but I can’t follow your logic. I’m not saying that it is wrong. I see what you are trying to say but, for me, there are too many intermediary steps missing from your argument for me to follow. For example, how do you get from a “lack” energy density to “we conclude that a negative energy-density must exist: DE.”

    I’m lost.

    …John

  25. #25 Charles Scurlock
    December 4, 2011

    Ethan deserves full credit for pointing out that the second law is conserved in any “closed system”. What is missing in this entire discussion is the question “What is the universe expanding into?” If the universe is finite, and I believe it is, as do many other cosmology thinkers, then it has, out there, somewhere, a boundary, an edge. I also agree that the common depiction, of an expanding sphere, is misleading. The Universe is not on the surface of a balloon, it’s what is inside the balloon! And the energy that is fueling the expansion is coming from the field it is expanding into, just as much of our energy is supplied from outside our little planet’s boundary. The tangle of using classical Newtonian mechanics is nice but the only thing it really proves is that (+1) + (-1) = 0, not that (+1)+(-1) = (some positive force, pushing us out away from each other).

  26. #26 Sascha Vongehr
    December 4, 2011

    Ethan, sit down some quiet evening and ask why you feel that “energy” should be conserved even in systems without such time-symmetry that demands conservation of such a mathematical quantity (or even have “energy” well defined). Energy is not holy cow urine:
    http://www.science20.com/alpha_meme/energy_not_golden_holy_cow_urine-72881
    E is useful if it makes calculations easier. At the point where we have to make headstands in order to rescue it into a realm where it is not applicable, it stopped having the use that made it classically important.

  27. #27 SCHWAR_A
    December 5, 2011

    @Johnfruh (24):
    …you really ask for the transition from “observed lack of energy-density” to “negative energy-density named DE”?

    Sorry, now I’m lost… I can’t find intermediate steps because “negative” is just a mathematical way explaining something, which is “missing”…

    Or do I misunderstand, what you are hunting for?

    Cheers

  28. #28 Chris
    December 5, 2011

    I think I understand DE exerting positive energy, and gravitation essentially performing the role as negative energy to balance the equation but I don’t understand how the universe continues to expand in a conserved system.

    I think my lack of understanding is how Dark Energy applies a negative pressure if the sphere is expanding

  29. #29 SCHWAR_A
    December 5, 2011

    Ethan,
    like Chris (26) I also see this problem:

    …I don’t understand how the universe continues to expand in a conserved system.

    Could you explain a bit the origin of the energy needed to continually expand, if there would be no DE?

    Thanks al lot in advance,
    Cheers.

  30. #30 David L
    December 5, 2011

    @25 Charles Scurlock

    “The Universe is not on the surface of a balloon, it’s what is inside the balloon!”

    From my understanding of the balloon analogy you have taken it too literally and completely missed the point of it with this statement. From the perspective of the two dimensional universe depicted on the surface of the balloon, there is no such thing as an “inside”.

  31. #31 Johnfruh
    December 5, 2011

    @SCHWAR_A (27)
    Thanks, You understand me perfectly. And there in lies my dilemma. You see, to me, “missing” means/equals zero while you say that “missing” means/equals negative! So, I’m still lost. What is doing the inverse of pressing?
    …John

  32. #32 Michael J. Burns
    December 5, 2011

    The Friedmann coordinates used in cosmology are noninertial and nonhomogeneous. The spacial coordinates are not geodesics. Observations mapped on to this system manifest fictitious acceleration, and thereby fictitious gravity and sources of gravity. If supernovae and accumulating intergalactic dust are not understood as evolving, in order to cover for a mere 10% variation in brightness, then a simple kinetic calculation shows a 10% cumulative slowing. This is contrary to the ballyhooed acceleration; which actually seems to be relative to an expectation of slowing that is even faster than what is measured.

  33. #33 The Peak Oil Poet
    December 5, 2011

    Wouldn’t it be a laugh if all of our attempts to explain an expanding universe where akin to the Ptolemy system of epicycles to explain the movement of planets – ie a basic assumption is wrong

    that would really shake things up

    what sort of assumption?

    well, how could i know – because i have the assumptions too

    but let’s make one up

    imagine that the speed of light is only constant relative to the gravity density at the point (or line) it is measured – ie imagine that in interstellar space it goes faster than it does in areas of higher gravity – and in intergalactic space it goes even faster

    and, if there was no gravity at all it would be infinitely fast

    so now we might posit that the red shift is the effect of light slowing down as it approaches areas of higher gravity

    and many other funny things in astrophysics might be explained

    suddenly we’d need no dark matter

    and no big bang

    that’s what i mean when i suggest that somewhere in all of our physics there might lie an assumption that we are blind to

    just as Ptolemy was blind to heliocentricity

    pop

    http://thepeakoilpoet.blogspot.com/2011/11/model.html

  34. #34 Hannes
    December 5, 2011

    The article seems to be referring in a strange way to Boyle’s law.

    http://upload.wikimedia.org/wikipedia/commons/thumb/1/15/Boyles_Law_animated.gif/220px-Boyles_Law_animated.gif

    In Boyle’s law when the total temperature of the universe is kept the same (would be like conservation of energy) then pressure[Gravity] and volume[Dark Energy] are inversely proportional. While the universe doubles its volume the pressure halves.

    Mass [gravity] and energy are like E=mc^2 . Thus one can read this as P = – ρ c^2 for Dark Energy.

    The problem that this analogy fails here imo is that the relative speed of the gas molecules in the contracted state are higher than in the expanded state. The gas molecules, if expanded to infinity would have almost no speed left.
    Pressure would drop to almost zero.

    This would mean there is hardly any energy left to move an object. Inertia would rule the universe. Energy production would be very difficult also. Coldness everywhere. Nobody would need a fridge!

    Since we see that in reality it is still much easier to start a fire by lighting a match than making ice in a fridge, we need real Dark Energy and no conservation of energy if we want to believe in this model of expansion.

  35. #35 SCHWAR_A
    December 6, 2011

    @Johnfruh (31):

    OK, now I got it (I hope…):

    Imagine the gravitational law as it is usually used and look at its non-zero-effect at very large distance.
    Sum up all these little non-zero-effects you expect, due to this usual law.
    Now you observe the actual behaviour and try to explain: you calculate from the observations that the “expected” non-zero-effects-sum is too big – you need to _subtract_ some effect, or, to add a _negative_ effect.

    With this _negative_ effect added to the system your calculation is OK and explains your observations.

    And now project this to DE…

    Cheers.

  36. #36 Johnfruh
    December 6, 2011

    @SCHWAR_A(35).

    Sorry, man. What you are describing is, it seems to me, a mathematical correction/manipulation. Be that as it may. What I am looking for is a conceptual understanding/meaning of negative pressure.

    What is it that can not on not be pressing but un-pressing?
    …John

  37. #37 SCHWAR_A
    December 7, 2011

    @Johnfruh (36):

    You think about an “un-pressing” or “sucking” DE as a physical something, which “creates” this effect independently from other things, quasi standalone or coming from external – correct?

    To my opinion this is not a good way to approach the phenomenon. If you go this way, you automatically will ask for the energy source of this “sucking”. But there is no such external energy source independent from other things in the universe! We have to explain the observed effects related to DE with all things we already have.

    So I would suggest to unbind from the literally interpreted “pressure” and “un-pressure” and concentrate to processes, which produce the same observational results within the universe system, but without adding doubtful external concepts. An one possibility is to replace “pressure” by “energy density”…

    Cheers.

  38. #38 Sinisa Lazarek
    December 7, 2011

    I agree that using the term “negative pressure” might not be the best description. I understand negative pressure when talked about it in day-to-day life. But when looked in that context, there is always another pressure to compare it to. i.e I can say that my room has negative pressure if it’s lower than atmospheric pressure outside. In the case of universe, this way of thinking about it is just wrong. After all, we don’t call magnetism negative electricity.

    Also, comparing DE as opposite of gravity, in my humble view, is also wrong. We don’t mesure the unit of rocket thrust as negative gravity. I understand that physicists mostly think through formulas and math. Math is the language of nature. However, great care should be taken in “translating” that language into our own talk. Lee Smolin said that math is only approximation of reality and as such should be carefully used because formula is one thing, reality is something else.

    I guess my point is that physicists should take care in choosing words to describe the math. If a “metaphor” or “symbol” is used, than it should be noted.

    Even here at Ethan’s great blog we all love and read daily, I see some “bad” comparisons. The one which prevails is comparing Universe to the sphere. And then physicists wonder how ordinary people can’t comprehend that the universe has no center. Well… if you tell people to imagine it as a sphere, then don’t be surprised about other things that go with it.

    I have no clue about what DE might be or even if there is DE. The pitfall is in the fact that all we measure and see is basically the past and not the present. We deduce that it must be accelerating today because of what we observe 3 billion years ago. If those distant supernovae stopped in their tracts this instant, we wouldn’t be aware of it for another 3 billion years. So any talk about the current state of the universe in my view only makes real sence if we talk about or solar system or our galaxy. Everything beyond that is speculation at best.

  39. #39 SCHWAR_A
    December 8, 2011

    @Sinisa Lazarek (38):

    I agree, except the last part:

    So any talk about the current state of the universe in my view only makes real sence if we talk about or solar system or our galaxy. Everything beyond that is speculation at best.

    To my opinion this is two-parted:
    yes, current state makes no sense, we cannot look into future.
    no, not everything is necessarily speculation. If you have a model describing the timeline based on lots of observed objects in distances (=pasts) like a chain, then you actually may interpolate without a big error.
    Thus gravitational effects observed far away from the past are about the same as those nearby, now. If we now observe a difference in behaviour of far away objects to those nearby, we have good reason to conclude that either the model is not complete, or there is something completely unknown.
    To my opinion related to DE the model of gravitational behaviour is not complete. We need some kind of Quantum Gravity to explain gravity itself – then finally we can upgrade our model…

    Cheers.

  40. #40 Lasse Holmström
    December 13, 2011

    Priset utdelas för upptäckten utav att universums expansionshastighet ökar och har nu bekräftas med ett nobelpris i fysik 2011. Genom att studera vita dvärgsolar med en massa som vår egen sol och storlek som vår jord samt med en tvillingsol i ett omlopp kring varandra, så har man upptäckt att en vita dvärgsolen tar materia ifrån tvillingsolen vilket inte är så konstigt då gravitationen på ytan av dvärgsolen är enorm och tvillingsolen har betydligt mindre grepp på sitt egna gasmoln. Jämför jorden med månen som inte har kvar sin atmosfär. När den vita dvärg solen har tagit åt sig en massa och når 1.4 solmassor så exploderar dvärgsolen och blir till en supernova typ Ia. Detta är något som händer väldigt sällan i en galax, en eller två gånger på tusen år.

    Men med hjälp att avsöka avlägsna supernovor med hjälp av en CCD laddningskopplad ljuskänslig halvledare detektor. Då man har nått en ljuskänslighet som fångar ca 70 procents av det infallande ljuset, som i jämförelse med fotografisk film som endast fångar 2 procent av det infallande ljuset så har det varit möjligt att redovisa nya resultat.

    Genom att kyla ned CCD så sänker man det termiska bruset i halvledarematerialet. Man kan också genom att öppna och stänga slutaren mappar man bort bruset ifrån den verkliga bilden. Genom att använda en bildförstärkare kan man utöka känsligheten så att en enda foton kan registreras.

    Genom att scanna stora områden på himlavalvet med hjälp av CCD teknik upptäckte de två teamen ungefär 50 olika supernovor av typ Ia samt att ljusemotionen var lika i alla de olika fallen så kunde man räkna ut distansen till supernovorna och bestämma den accelererande expansionen. Detta hade till följd att den förväntade avstannandet av expansionen på grund av gravitation inte stämde utan att resultatet av accelererande expansionen endast kan förklaras med en 75 % mörk energi och en 20 % mörk materia som finns närvarande någonstans i universum.

    En möjlig förklaring kan vara att om man tänder ett ljus och det är det enda som finns i universum i det ögonblicket, så kommer ljuset eller riktigare, den elektromagnetiska vågen som består av fotoner som partiklar eller våg rörelse, att expandera åt alla håll som i en “ballong” som man blåser upp med ljusets hastighet från källan i centrum av ballongen. För en iakttagare som befinner sig i rörelse någonstans mellan centrum och ballongens med ljushastighetens expanderande kant, så är allt som existerar åt andra hållet, ej någonsin är möjligt att upptäcka, på grund av att ljuset inte hinner ikapp sig själv. När våg och foton-ballongen utvidgar sig skapas höjd, bredd, längd och tid i ett icke innan rumsbaserat tomrum, man kan därefter mäta tid och rymd. Detta alternativet står inte i samklang med etablerad fysik, för det finns inte någon fysisk mekanism som tillåter att den elektromagnetiska vågen skapar rumtid på det sättet. Men ändå så påstår jag att det är på det viset. På den plats iakttagaren befinner sig, skapas således ett universum som är en del av den totala “ ballongen”.

    Man kan grovt likna vårat universum som en klyfta i en apelsin med 5 % massa.

    Lite mindre grovt blir det om man undersöker den bästa kartan hittills av den kosmiska bakgrundsstrålningen, CMB det så kallade ekot av Big Bang. Med hjälp av kartan så visar universum att det inte kan vara samma strålning i alla riktningar. Man hade förväntat sig att bakgrundsstrålningen skulle vara isotrop, utan någon särskild riktning i rymden, men så var det inte.

    Om man tittar på symmetri i CMB strålningen så kallas den för octopole ellerr quadrupol och det var ett märklig mönster.Man hade inte förväntat sig något mönster över huvud taget. Men det man såg var allt annat än slumpmässigt det såg ut som en fotboll. Den var octopole och quadrupol komponenter som var placerade i en rak linje över himlen, längs ett slags kosmisk ekvator. Det är ovanligt.

    Totalt så finns den stora eftersökta massan i de övriga klyftorna eller fotbollarna.

    20 fotbollar formar ett multiuniversum klot där den saknade mörka energin och massan finns. Så kan dessa 19 fotbollar eller 19 klyftor ses som parallella värdar till våran värld i “ballongen”. Vi kan observera effekterna av den mörka energin överallt i universum genom att studera hur stjärnorna rör sig i ytterkanten av en galax eller hur galaxerna rör sig i en galax hop. I båda fallen märker vi att stjärnorna och galaxerna rör sig för fort, det vill säga vi ser att de rör sig snabbare än om de bara påverkas av gravitationen från den synliga materien. Det måste alltså finnas mörk materia som bidrar till det gravitationsfält som påverkar stjärnorna och galaxerna och det finns i samtliga “klyftor eller fotbollar”.
    Nu kommer det riktigt paradoxala i den här upptäckten. Gravitationens påverkan på expansionen förändras inte så mycket med tiden, utan det är gravitationens i stort sett konstanta påverkan som leder till att universums expansion accelererar. Hur går detta till? Jo, enligt Einsteins allmänna relativitetsteori är det energidensiteten, rho, och trycket, p som tillsammans utgör källan till gravitationen genom sambandet rho + 3p. I de flesta sammanhang som vi är vana vid är trycket försumbart litet jämfört med energidensiteten, men för mörk energi är p = – rho i det enklaste fallet, så trycket är inte bara negativt (däremot kan energidensiteten aldrig vara negativ) utan så negativt att rho + 3p blir negativt, och då blir gravitationen repellerande och vi får en accelererande expansion. Dessutom är det så att i det enklaste fallet, som jag visar ovan, så fylls det på med ny mörk energi i det nya rummet som bildas allt eftersom universum expanderar, så den blir aldrig ens förtunnad!

    Saknar Ariel Goobar och Carl Pennypacke vid nobelprisutnämningen i fysik 2011

    Bra länk: http://news.bbc.co.uk/2/hi/science/nature/2814947.stm

    Universum skapas när den elektromagnetiska vågen expanderar med ljushastigheten. Då kan man lägga i den bubblan en tumstock och mäta höjd längd och bredd samt tid.Vågen skapar rummet och tiden i ett icke rum eller i ett ingenting. Stick hål på bubblan och dra ut universum ur punkten. Man vränger universum ut och in så att bakgrundsstrålningen blir en mittpunkt i stället för våran vintergata. För åt vilket håll vi nu än tittar så är det start punkten som vi ser i ett krökt universum. Då är vi 13 milj. ljusår ifrån startpunkten. Den strålningen som har gått åt andra håll skapar sina egna universum skilda från oss därför att dess ljus aldrig når oss någonsin. Men massa finns ju i dessa universum och påverkar vårat universum. Kan man kalla den massan för den saknade svarta massan? Universum är det vi ser och iakttager, men så mycket mera finns utanför denna iakttagna horisont.

  41. #41 nouman
    January 17, 2012

    the most and best possible to explain what it is! i hope all will be happy with this explanation
    all the best

  42. #42 Brad
    February 2, 2012

    i believe very strongly that we are microcosm of everything think about how all gasses will expand forever until they have spread so far you can no longer see any trace of the gas due to diffusion but the gas still remains in very small quantities.all im trying to say is that just like a puff of smoke will always expand so will our universe

  43. #43 Johnleprekan
    USA
    September 24, 2012

    How does the negative pressure become greater than the gravitational attraction?

  44. #44 Johnleprekan
    USA
    September 24, 2012

    What is the dark energy pulling on if it is spread out? Should the expansion cause the pull to get weaker?

  45. #45 Wow
    September 24, 2012

    The first question is nonsensical. The second one can be answered.

    Yes, but it doesn’t seem to be getting weaker. There’s no rule it must, except by default you may expect it. But the energy may be coming from the drop in gravitational potential energy as the universe loses its edges over the edge of where information can come from.

    Some questions are nonsense, some just not (yet?) answered, in the latter we may have observations and a tentative theory, but no genuine answer.

  46. #46 Ben
    Melbourne, Australia
    December 16, 2012

    Here’s how I understand the effect of negative pressure:

    In GR, Einstein showed that gravitational force depends not simply on mass, but also heat and on pressures exerted (pretty obvious why this is true).

    Outward directed pressure (positive pressure) contributes positively to the gravitational force, whereas negative pressure (inwardly directed pressure) contributes negatively.
    Dark energy is one source of negative pressure.

    Given that gravitational force btw bodies is directly proportional to the product of their masses, and inversely proportional to the square of the distance between them, at a certain point the negative pressure contributed by dark energy is enough to overcome the positive gravitational force of matter. ( This is then coupled with the exponential decrease of the universal attractive gravitational force due to the linear expansion of the universe (i.e given expansion, the square of the distance between the ‘centre’ and the circumferece (or outermost perimeter, if you prefer), that which is the denominator of the eqaution, is increasing exponentially. Hence attractive gravity and it’s ability to overcome the negative gravity of dark energy.
    Once attractive gravity is equal to repulsive gravity (negative pressure of dark energy), a qualitative tranformation in the expansion of the universe happens and the expansion accelerates.

    At least, that how I understand it.
    Please correct me if I’m wrong.

  47. #47 Mike
    January 21, 2013

    When mass warps space between objects locally it effectively reduces the distance between them. That’s what gravity does. It draws masses toward one another. Now let’s assume that the “distance” between all the objects in the universe has to remain constant. Space has to expand to maintain the constant distance. Gravity continues to act so space continues to expand.

  48. #48 Wow
    January 21, 2013

    “Here’s how I understand the effect of negative pressure:”

    Negative pressure is almost exactly like negative temperature.

    Because of the definition of where it is used, it makes sense.

    But only because it is meant to be used in that context.