"The greatest enemy of knowledge is not ignorance, it is the illusion of knowledge." -Stephen Hawking
The Universe is a vast, seemingly unending marvel of existence. Over the past century, we've learned that the Universe stretches out beyond the billions of stars in our Milky Way, out across billions of light years, containing close to a trillion galaxies all told.
And yet, that's just the observable Universe! There are good reasons to believe that the Universe continues on and on beyond the limits of what we can see; the question is, how far does it go on? Forever? Or does it close back upon itself at some point?
To help us better understand this question, let's turn to something more familiar (and smaller) that we know how to measure the size of: the Earth.
 Image credit: Tom of http://apacificview.blogspot.com/.
Image credit: Tom of http://apacificview.blogspot.com/.
From the top of a tall mountain, like Mauna Kea, shown here, you might hope to measure the Earth's curvature, but your efforts would be in vain. From even 14,000 feet up, the curvature of the Earth is totally indistinguishable from flat.
There are images out there where the Earth appears curved when you look out at the water, and indeed, they're not hard to find. But is that because of the Earth's curvature?
Not at all; it's because of atmospheric distortion. If you were to try and calculate the circumference of the Earth from a photo like this, you'd get a world that was smaller than even the Moon is; you cannot measure the curvature of the Earth from any known location on the surface of the planet.
What's more than that is that, over land, the Universe isn't perfectly smooth. Some places are curved upwards, others downwards, and any small region visible to you is unlikely to be a fair representation of the entire planet.
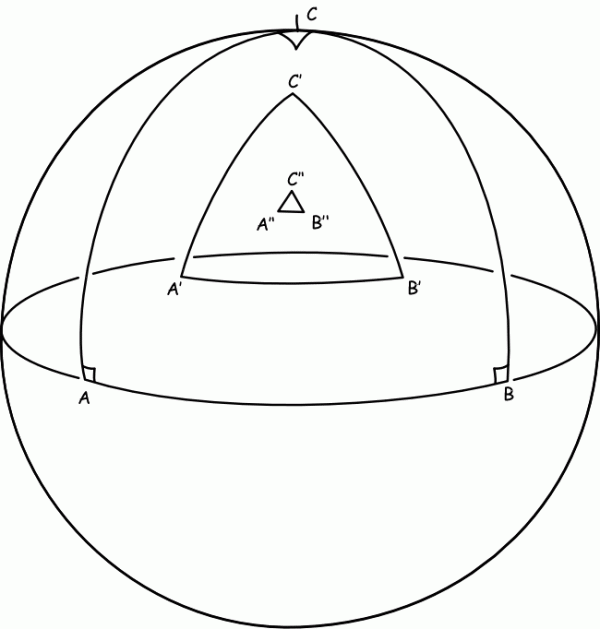
There is a way that you'd be able to tell, though, what the shape and size of the planet actually is. All you'd have to do is take the appropriate measurements and use geometry.
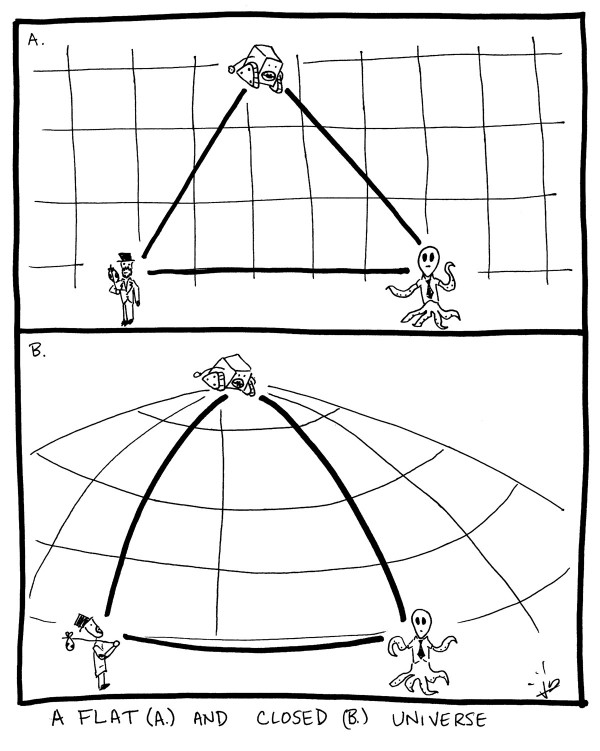
It's as simple as going to three separate locations on Earth and drawing a triangle to connect those three points.
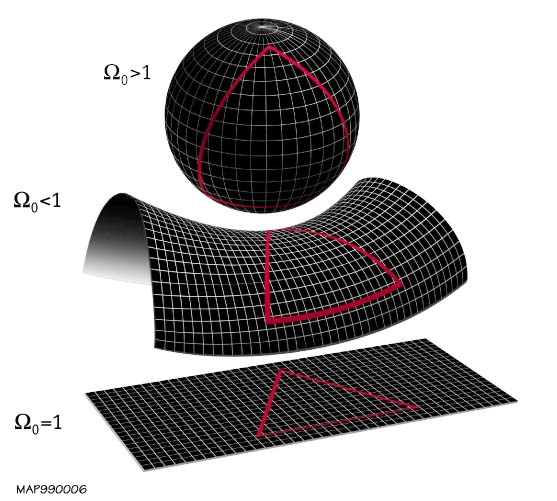
On a flat sheet of paper, the three angles of any triangle will always add up to 180°, as you well know. But if you're on the surface of a sphere (or, mathematically, any surface of positive curvature), those angles will add up to more than 180°. Knowing the distance between each of those three points and the measure of all three angles allows you to calculate what the circumference of the Earth is.
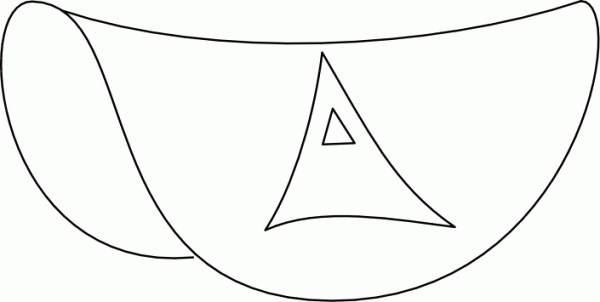
And, of course, the farther away your three points are from one another, the less important the mountains, valleys and oceans are, and the more important the overall shape of the Earth is to your measurement. The converse would have been true if the Earth were shaped with negative curvature, like a saddle, as shown below.
A surface of negative curvature has any three points form a triangle whose three angles sum to less than 180°, and again, knowing the distances and measurements of all three angles allows you to calculate the radius of curvature.
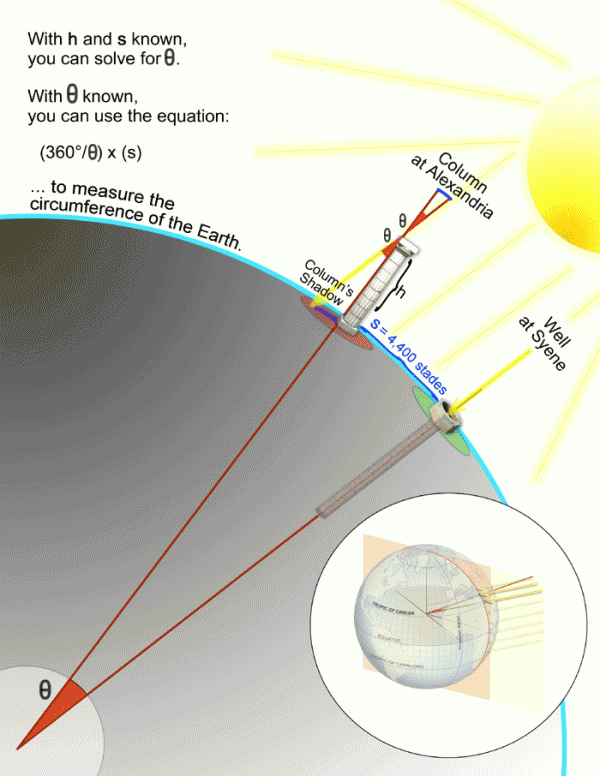
In practice, the very first calculation of the circumference of the Earth -- dating to the 3rd Century B.C. -- used a very similar method, again reliant on simple geometry.
It would not be until the 20th Century that we were actually able to achieve altitudes capable of measuring the curvature of the Earth from space, something we are only able to do because we can step off of the two-dimensional surface of the Earth and look at it from afar.
By 1948, we were creating mosaics of the Earth by stitching together multiple images of the Earth from space, and there could no longer be any doubt as to its circumference.
But space itself is a little trickier. Yes, it is just a geometric construct (albeit a slightly more complicated one), but it also has an inherent curvature to it. The amount that the space of our Universe is curved is directly related to the amount of matter and energy that we have in it.
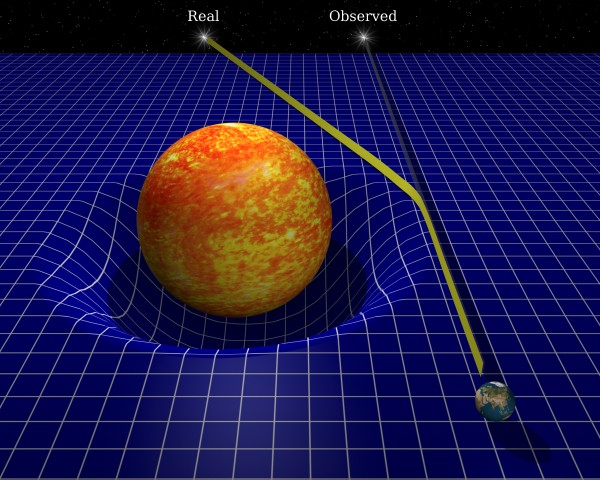 Image credit: Dave Jarvis of http://davidjarvis.ca/dave/gallery/.
Image credit: Dave Jarvis of http://davidjarvis.ca/dave/gallery/.
(Link to David Jarvis' gallery.) Dense, heavy masses like the Sun cause very large amounts of curvature in very small spaces, significant enough to bend starlight by amounts significant enough you could notice it with 1919's technology. But that's local curvature, the same way mountains, valleys and oceans are local curvature here on Earth; what we're interested in is whether the entire Universe ever closes back in on itself, and if so, how big it is. In other words, these local sources of curvature are things we need to not be fooled by.
The Earth, too, curves the spacetime around it. Remember that we use two dimensions as an illustration, but unlike measuring the curvature of Earth, where we can fly "up" and observe the planet below, there is no extra dimension to move through to step back from the curvature of space.
All of the spatial dimensions are curved. Since stepping back from the Universe and observing it from afar isn't an option, the only way to get a good handle on its curvature is to examine it on its largest scales, and try to infer its geometry.
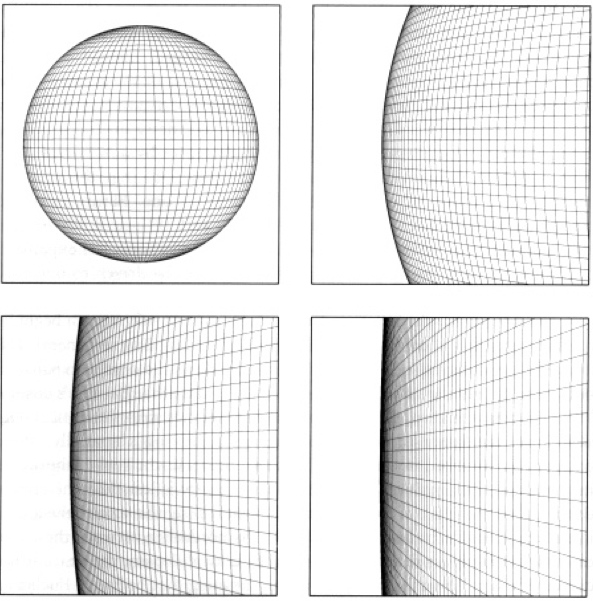
In principle, this is pretty straightforward. Just as any three points on a surface can help you calculate that surface's curvature, you can do the exact same thing with the Universe! Take any three points that are far enough apart, measure the distances between those points and the relative angles between them as well, and you'll be able to figure out not only how your spacetime is curved, but also what the radius of curvature is!
You can imagine three possible cases, of course. One is where the Universe is positively curved, like a higher-dimensional sphere, one is where the Universe is totally flat, like a higher-dimensional grid, and one where the Universe is negatively curved, like a higher-dimensional saddle. In the context of general relativity, it's the energy density -- the amount of matter and all other forms of energy -- that determine this curvature.
In real life, we don't have man-made objects far enough away to communicate with us across the necessary distances to measure curvature. Even if we did, it would take billions of years to do it, which is a disheartening way to attempt to do science. But we have light signals from when the Universe was just 380,000 years old, that tell us what the Universe is like 46 billion light years away.
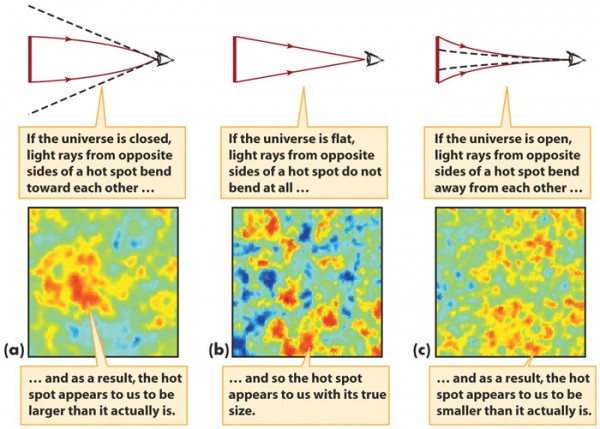
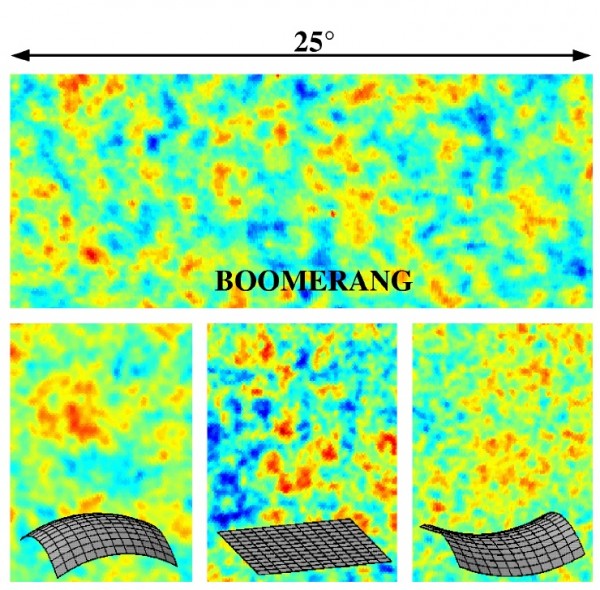
The fluctuations in the cosmic microwave background -- the leftover glow from the big bang -- provide a window allowing us to see how our Universe is curved.
The first robust measurements of this came from the BOOMERanG experiment in the late 1990s (hearing Paolo de Bernardis talk about this in 2004 was a highlight for me during the early stages of my scientific career), where they first determined that rather than having significant positive or negative curvature, the Universe was indistinguishable from flat.
That doesn't mean that it is flat, of course. If you walked outside and tried to measure the curvature of the Earth right now, but only within 5 km (or 3 miles) of your current location, you would find that the Earth is consistent with being flat, but it could also be positively or negatively curved on a larger scale than you're currently measuring.
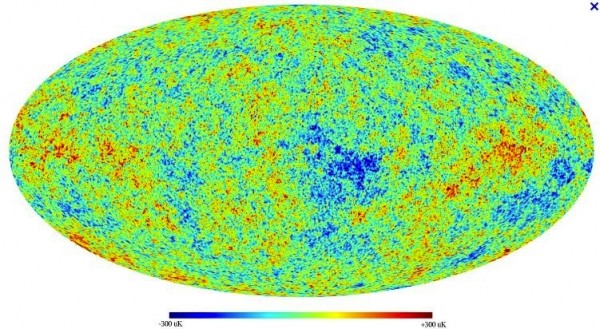
So it goes with the Universe as well. We were able to measure that the Universe, if it is curved, has a much larger radius of curvature than that of our observable Universe, which is about 46 billion light years. But if we could make that measurement more precise, we could conceivably measure a much smaller curvature than even that. Thanks to the WMAP satellite, we now have the temperature fluctuations over the entire sky measured at a very narrow, less-than-half-a-degree resolution.
And what they teach us is that not only is the Universe consistent with being flat, it's really, really, REALLY flat! If the Universe does curve back and close on itself, its radius of curvature is at least 150 times as large as the part that's observable to us! Meaning that -- even without speculative physics like cosmic inflation -- we know that the entire Universe extends for at least 14 trillion light years in diameter, including the part that's unobservable to us today.
Just because the part of it we can see is indistinguishable from flat doesn't mean it's intrinsically flat in its entirety. But it does mean that the Universe is far larger than we'll ever see. Even taking the minimum allowable estimate for the size of the Universe means that, at most, less than 0.0001% of the volume of the Universe is presently or will ever be observable to us. Once you put our knowledge about dark matter and dark energy in there, you'll realize that we'll never see more of the Universe than we can right now.
So all that we see -- the billions of stars in our galaxy, the hundreds of billions of galaxies lighting up the observable Universe -- is just a teeny-tiny fraction of what's actually out there, beyond what we can see. And yet, we can know that it's there. Isn't science wonderful?
- Log in to post comments











Do we know if there are any stars, planets, and other objects in the unobservable part of the universe?
Or will we never know?
I've gone through parts of this argument myself, explaining cosmology/CMB stuff to my non-physicist friends and family. Reading it now, it occurs to me that there's a little piece I don't quite get :-(
Your figure on the CMB fluctuations (from the Smoot group at LBNL) talks about comparing the "observed size" of hot-spots (for example) to their "actual size." For a flat universe, we see the hot-spots at their actual size.
But _how do we know_ their "actual size"? Is the intrinsic size of the fluctuations something that is determined a priori? If so, how, and what is the uncertainty on that calculation? Or is it model dependent?
@Michael Kelsey: As a layman, over the years I've found that Mr Siegel's posts occasionally have a key blind spot (or two, or three...) for me, but maybe I didn't get lost this time, I'll give it a stab.
We know that the light from the CMB is around 13.7 billion years old. We also know that the CMB "flash" occurred around 100,000 years after the Big Bang, so this gives us a pretty good estimate on the size of what we're looking at, as well as the features within.
Then considering that in the WMAP image, blue is 2.721 Kelvin and red is 2.729 Kelvin, the CMB is ridiculously smooth. We may not be able to infer a maximum size from this, but a minimum is at least implied in the parameters and data.
Is that more or less the idea?
Nice post but could you explane how atmospheric distortion produces curved like horizon?
It could be very very big and flat, but mostly empty. The bit we can see may not be representative.
First I would like to tell you that you blog is definitely the best science blog ever. I consult it on a daily basis.
Second; A small question.It is my understanding that closed and flat topologies are possible. (like a higher dimension torus) Is this type of topology still considered a candidate? If yes, am I wrong saying that finally it can be much smaller after all?
A very interesing post indeed.
I assume bubble or pocket universes in inflation can be intrinsically flat as well?
@ Eric:
Inflation would make our universe expand to that size. This would make our observable universe a small sample out of a larger region. Bar an unlikely conspiracy, it would be a representative sample.
It is beyond that things may conspire to be different I guess. But theoretically there are reasons to believe it would be homogeneous, as some theories are as I understand them.
On top of that, if bubble universes exist, they may be intruding at light speed and not be seen before they hit us. Again, unlikely compared to the vastness and age of a universe. It hasn't happened in 13 billion years.
@ Michael Kelsey:
Primordial fluctuations follow a power law for the Fourier components and yes, somewhat model dependent though the exponent is measured (roughly "the scalar spectral index" - fluctuations are scale invariant). [Wikipedia.]
Presumably the curvature effect makes a linear systematic effect, which would be a triangular window on spatial scales and so convolution would give a 1/n product with the components unless I am mistaken.
TL;DR: It would look like the wrong power law?
@ The Bad Wolf:
The density gradient with height would make a difference in principle, but I would guess the temperature gradients overwhelms, see mirages.
Trivia: In actuality outside measurements, our brains are wired to perceive the sky as a fish bowl, flatter than a spherical envelope. It makes the best prediction of why we see a Moon near the horizon as larger. (HT Bad Astronomy.)
@ Michael Kelsey: Oops. Nitpicking myself: More precisely, fluctuations are *nearly* scale invariant. The difference is still physically important as I understand it. (Inflation vs something else.)
Which is why we could suspect "wrong power law" at the very least, if there are no other means.
@Michael Kelsey: We can, as Torbjörn points out, measure the spectrum of the fluctuations as a function of l, which is inversely proportional to angular size. (It's the same l used to index spherical harmonics.) We can also measure it separately for points above and below the average. The latter two spectra should be, within statistical error, identical to each other if the universe is flat. If the hot spots show a statistically significant tendency toward lower (higher) l than the cold spots, that would be evidence of a closed (open) universe, as there is no reason this difference should be present in the actual size distribution. The statistical error in the measurement is what gives us a lower bound for the scale of any curvature which might be present.
"The bit we can see may not be representative."
The bits we can't see, don't exist.
As in there's no way for them to influence us, nor for our observations to be influenced by them.
To all intents and purposes, they don't exist.
@Torbjörn Larsson, OM: Thanks. Why didn't I figure it out myself, if that's the case? I've read Phil Plait's BA explanation of the big moon ilusion
There seem to be estimates of the size of the universe when it is less than a second old, but no size figures later on, say when the CMB was made. Is this because of inflation? If not, what? I'd like to see a timeline of the universe that includes size.
Doesn't space have to have a positive curvature as it expands uniformly in all directions? If not, why? If we could measure the curvature, would this tell us how big the universe was at the moment of the CMB?
What does it mean to say that space would curve back on itself? It doesn't make sense that there would be a spherical surface at the edge of the universe and you could travel through that space in a straight line with your space ship, ending up where you started, whereas if you were back a bit from the edge you'd have to steer in a big circle to do the same thing. Being at the edge of the creation of space would be different than that. Wouldn't the leading edge of the universe have to be creating space faster than the speed of light?
"What does it mean to say that space would curve back on itself?"
Go West, young man.
If you have a suitable method of walking on water, you will end up back where you started, the path taken having curved back on itself.
Re: the discussion about how we know what's "actual size" vs. the observed size of the fluctuations.
We know what the amplitude of the large-scale fluctuations is (and have since COBE) and also just how scale-invariant the initial fluctuations are.
But 380,000 years is a long time for gravity on small scales, and so that famous pattern of fluctuations -- with peaks and troughs -- tells us a lot about the energy composition of the Universe. How much is dark matter, how much is dark energy, how much is baryonic matter, how much is photons, and how much is spatial curvature.
The CMB can't give us all of that info on its own (there are degeneracies), but as of 2011 here is what the CMB alone tells us: http://astrobites.com/2011/05/04/can-the-cmb-alone-provide-evidence-for…
The dotted line is a flat, 100% curvature-free Universe. When you combine large-scale structure data, the known value for the hubble constant and supernova data, that allows you to get the constraint that the Universe's curvature is such that the total size of it all is at least 150x the observable size.
Eric Lund pretty well summed up how you can predict the maximums and minimums of variance using spherical resonane equations, but I wanted clarify one thing. The reason this suggests inflationary cosmology is because the resonance matches the patterns you would expect if cooling occured at a quantum scale with uncertainty and quantum fluctuations taken into account. In a non-quantum world, you would expect a perfectly uniform temperature density because the temperature would have been homogenous across all space, but little quantum fluctuations early on would cause temperature variance in a predictable way. cosmologists suggest that matching the resonance in temp variance of the whole universe with the resonance in temp variance predicted by quantum mechanics along with other aspects dealing with the age/observable size of the universe are proof of their inflationary model.
Terrific article! So you are saying the entire universe is at least some 1 million times larger than the observable universe. Correct?
"The Universe is really really really flat" ..."the entire Universe extends for at least 14 trillion light years in diameter". Uhm, I'm confused. How can it be so flat, AND have a (huge) diameter?
Mark V2:
Simple, really -- a very huge diameter means the surface is very close to being flat. Not *perfectly* flat, but really really really flat.
So flat that it's exceedingly hard to tell for certain if it is actually curved at all or really, perfectly flat. As Ethan said, this is an upper bound on curvature -- our measurements say the universe has to be *at least* this big in diameter. It may actually have infinite diameter, and be perfectly flat.
But it's nearly impossible to tell. And that means, at least, that the universe is really, really, really flat.
Hope that helps. :)
Thanks for answering a question that always intrigued me.
Now you mentioned cosmic inflation.
Is there a theoretical lower bound to the size of the (whole) universe according to inflation ?
Ethan good summary.
For me the question is: what is the shape of the large scale spacetime topology of the universe?
So the spatial analogies of a spatially curved earth and spatial curvature of the visible universe are not enough; spacetime curvature must be considered (not just spatial curvature) and spacetime orientability or nonorientability must be considered.
A Moebius strip or Klien bottle are examples of nonoreintable topologies that are locally Euclidean.
http://arxiv.org/pdf/gr-qc/0202031v4.pdf "Contrary to established beliefs, spacetime may not be time-orientable. By considering an experimental test of time orientability it is shown that a failure of time-orientability of a spacetime region would be indistinguishable from a particle antiparticle annihilation event."
http://arxiv.org/abs/gr-qc/9901016 "the main motivation for the study of nonorientable spacetime tunnelings is related to the notion of the so called quantum time machine which, together with virtual black holes and Euclidean wormholes, appears as a necessary ingredient for a consistent description of the quantum spacetime foam"
I'm not arguing that these papers on nonorientable spacetime are correct. I'm agreeing with these papers that restricting the discussion of the topology of the universe to orientable spaces or oreintable spacetimes models may be too restrictive.
"The Universe, if it is curved, has a much larger radius of curvature than that of our observable Universe, which is about 46 billion light years." You used that figure twice in the post, Ethan, and that's the first time I've seen it. I thought briefly you meant 13.75 billion x π, but that doesn't work. Are you factoring in a period of faster-than-light spatial expansion? So when we look as deep as we can into space, we see what happened close to 13.75 billion years ago, but any actual objects we see are now 46 billion light-years distant? To my mind, that only works if the faster-than-light expansion also affected the photons that were in that space, pulling them along "faster than light." And I still don't see how the unobservable-to-us part of the universe got so big so fast. You've thrown my entire worldview into disarray, Ethan. Thanks a lot.
@Chuckinmontreal, Ethan wrote a post about that once, can't find it now. In my understanding, light always moves at the speed of light in local space. But in the cosmic scale, the space itself expands, so the "new" space appears between us an photons traveling in our direction. This is why the distance between us and the photon decreases at slower rate than c. And the farther away the photon is, the slower distance decreases.
@Ethan, please forgive potentially naïve question, but...
You make an assumption, that if the Universe has positive curvature it must be closed. Isn't it an analogy to the Earth, which doesn't have to work for the Univers? Earth is closed, because it has positive curvature AND is embedded in three-dimentional flat space. But as far as we know there is no four-dimentional flat space that contains our Universe, so Universe does not obey geometry of that space. Can't it be the case that Universe has positive curvature, but still is open?
Question: We assume the universe is 13.7 billion light years old. And according to Wolfram Alpha the diameter of the observable universe is 93+ billion light years. I am not catching on. If I was the center of the universe and the universe went out 13.7 bill light years to my left and to my right, wouldn't the diameter be 27.4 bill light years? please help.
Thank you.
@Chuckinmontreal and @Bob - You can read Ethan's old post about how even though the Universe is only 13.7 billion years old, we can see things that are 46.5 billion light years away.
http://scienceblogs.com/startswithabang/2009/07/31/the-size-of-the-univ…
Hi there! This was an excellent blog post. Very informative and thouhgt-provoking. However there is one part in your argument where, to my eyes, you take on a presupposition without properly explaining why:
For the entire last section of your post, you explain that IF we assume a universe that curves back on itself, we can use our measured lower bound for the curvature of spacetime to calculate the smallest possible radius for the universe. I got that part. However that's a pretty big 'if', which I felt you grossed a bit over. Is't it just as likely that the universe is flat, finite, and ends just beyond the horizon of visibility? Couldn't it be curved (negatively or positively) but just end before it completely curves back on itself? Are these ideas that astronomy doesn't favor because a physical "end" to the universe is not an appealing idea?
Or are there other observational reasons that favor a closed universe?
Thank you!
From the big bang 13b years ago , the size of a proton to over a trillion light years in diameter ! At what speed would the universe be expanding and can we measure that ?
If the expansion is getting faster it must have been very slow in the beginning.
Why do cosmologists use so many mundane terms without precisely defining them? It arouses great skepticism.
I am gradually convincing myself that the confusion over flatness is driven by an attempt to apply classical reasoning to a non-classical situation. We have now confirmed that the masses of particles are generated by local phenomenon and reflect the interaction strength of a particle with the background Higgs field. In QFT we can interpret composite entities (such as hydrogen) as independent particles. Since a bound state of particles has less rest mass than its components, this means that the interaction of the composite state with the background Higgs field is less.
In larger charge and color neutral composite particles, like solar system, or the earth and moon, we obviously have gravity, and again the composite interaction strength with the Higgs field is fractional smaller than the interaction strength of all the independent components. Once again, all the interaction events are localized, and the local space is flat. That we mentally interpret that as curvature is just a reflection of our ability to measure the differences between local interaction strength of large composite particles versus there independent components. A priori there is no real reason not to see the local space as flat, since the Higgs field must be uniform since it is scalar.
It should be clear then that gravity is a relative measure of covariance, and our objective is to clarify what the definition of independence of particles is.
So let me get this straight. All the observations show that the universe is flat. But we don't want that to be true. We want the universe to be round. But in order for that to be true, we must postulate that the universe is much larger than our observations show. Therefore, the universe is much larger than our observations show.
And if anyone says, "Uh, how's that?" then just throw in a platitudinous non sequitor about how it's not so unusual, because after all, we can't observe dark matter either.
This is why cosmologists are viewed by other scientists as unscientific flakes.
Re: Wirlwind; yes, we only 'know' the Big Bang was the beginning of "substance" (matter, energy, dark matter, dark energy) because we have measured the expansion of 'stuff' not the expansion of the universe. It seems entirely reasonable to me that the "universe" didn't start with the Big Bang, the 'stuff' we find in the univers started then.
Who said anything about "want", apart from you, that is, WM.
Is it that you want to make believe that science is all make believe?
Many years ago I read that if you took a paper plate and put a dot in the center of the bottom of it and took your grandkid into the front lawn and laid the paper plate on the ground upside down and then explained "The dot is our solar system which includes the earth and the edge of the paper plate is the edge of the observable universe and the earth that it sits upon is the Universe". Sounds as good to me as anything else I've heard and a simple and beautiful way to give a child something to think about. Of course this implies a round universe, still it also implies immensity beyond on a grand scale regardless of flat or round. I like the round Idea, but then I also prefer blue over green and yes over no, so go figure.
Then again it could all be BS and the TRUTH will one day win out. Good Luck.
He stated that the universe's diameter is at least 14 trillion light years, which means its radius is 7 trillion. The age of the universe (according to the best estimates) is about 14 billion years. So if I'm thinking right that would mean that either space traveled faster then the speed of light (and significantly faster), or the math in one of these two estimates is wrong.
Or am I just looking at this wrong?
Photographs of Earth from space in 1948? Wasn't the first artificial satellite launched in 1957?
maybe the universe are a colision of branes on S form and acelerates and finaly retracts. OR lS a colision of a super gigaNtesc massive galaxy THAT IS OUR UNIVERSE.
THE PERSPECTIV IS DIFERENT.
you cannot measure the curvature of the Earth from any known location on the surface of the planet.
That is actually wrong. Not only was there Eratosthenes (and various others over the centuries) who measured the curvature of Earth within a precision limited by the technology available to them, but today if one has access to a body of water that is dammed off and knows how to use the right equipment (affordable as second hand gear in our modern society), one can make this kind of measurement oneself.
When measuring the dynamic kinematic SZ-effect [Sunyaev and Zel'dovich] it reveals that the average temperature difference between any number of galaxies in the CMB radiation shows that clusters are slightly more likely to be moving towards each other than away from each other [Ostriker–Vishniac effect]. See http://arxiv.org/abs/1203.4219 .
How is this possible in an expanding universe with 'Dark energy'?
Maybe it ins't possible, Hannes, and that paper is wrong.
Hannes,
I don't think it's wrong, it has been in the news for some time now and the article is soon to be published by the Physical Review Letters. (http://www.nature.com/news/galaxy-clusters-caught-in-motion-1.10920)
Its an interesting paper, but nobody says that it is in contradiction with the Big Bang (expanding universe). I have always found such a concept strange for many reasons, one of them is because locally our Milky Way and the Andromeda galaxy are moving towards each other.
Indeed it would be interesting if someone could give an explanation why these findings would be in-line with Big Bang theory.
The paper doesn't say what you say it does, hannes:
"The conventional scenario of structure formation, driven by gravitational attraction, predicts that any pair of clusters should have a slight tendency to be moving towards each other rather than away from each other [17, 18], and we see the expected signal in our data at a statistical significance of 3.8σ."
Hence your assertion that this isn't possible in an expanding universe is not bourne out by the paper.
For those who still question the finitenes of our universe I once heard this explanation. A universe infinite in space must also be infinite in time (A head exploder warning!). Therefore light would have been travelling from everywhere forever and instead of seeing individual stars in a black sky we would have a pure light sky since light has been coming from everywhere, forever. Therefore we must have a limited Universe.
Is it necessarily true that the radius of the universe is equal to its radius of curvature? I think the article confuses them near the end.
If the universe if 14 billion years old, why wouldn't its radius be 14 billion light-years?
@Paul: That would be true, except for the fact that objects accelerating away from us have their light redshifted to lower energies, until they're undetectable (wavelengths longer than the observable universe's diameter). Add that to the fact that the furthest objects are actually accelerating away faster than the speed of light due to the metric expansion of space, and those objects become doubly invisible.
@BentFranklin: though the BB happened 13.7 billion years ago, inflation followed immediately after, so that explains why our observable universe is 46 bly across, and the big U Universe is at least a trillion (and perhaps infinitely large).
I think I missed something. The last part about the universe being at least 14 trillion light years in diameter. Is that only if the universe curves back on itself, or do we know it's curved?
I don't think the curved appearance of the horizon in photos is due to atmospheric effects.
It's due to the fact that a straight line in 3space perspective projected onto a 2d plane creates a curved line. This is more pronounced when the 3line is long, and extends either side of the point of closest approach to the viewer. Hence it is especially noticeable when a wide angle lens compresses a wide field of view into a small photo. This would occur without any atmosphere.
I challenge your notion that "From even 14,000 feet up, the curvature of the Earth is totally indistinguishable from flat"
Just got back from vacation. In the 3rd-floor beachfront condo I was staying at, you could EASILY observe the curvature of the earth over the ocean (where there are no obstructions). We aligned our line of sight with a fixed level line (the balcony rail) to match the horizon perfectly. Looking left and right to the extremes of the balcony, you could see the round curvature of the Earth.
I believe what you were inferring was that because the mountain did not tower above its surroundings enough, it was not visible...
The Iacopino picture is more confusing than helpful, especially lacking a concrete definition for "curvature" in three dimensions. I *think* it's trying to use the third dimension both as the actual third dimension (giving the earth and sun volume), and also showing the curvature of space. But I'm not sure. I don't think there is an actual "bottom" that has a pit, like a cupholder in my car, in which the sun sits.
"we’ll never see more of the Universe than we can right now"
I'm not sure what this means.
* http://davidjarvis.ca/dave/gallery/
* http://davidjarvis.ca/dave/gallery/lg/gravitational-lens-01.jpg
I am the original author of one of the images you used, not Francesco.
Please:
1. Change the image credit attribution from Francesco Iacopino to Dave Jarvis.
2. Provide a link back to the gallery: http://davidjarvis.ca/dave/gallery/
3. Remove the high resolution version from your server.
Dave,
Thank you for correcting the image caption and for providing the links to yourself and your image.
My apologies for getting it wrong initially; I normally try to do my due diligence to get the attribution correct, and I'm sorry I was unable to do so in this instance.
The image credit has been changed, and I have included the URL back to your gallery.
With the recent scienceblogs migration -- and this is embarrassing -- I do not know how to delete a file from the server. As soon as I can figure that out I will make it happen, but I assure you I am trying to address it.
Update for you: What I can do is make it so that a click on this file links to your site rather than the file here. Hope this is satisfactory to you, and thanks again for creating such a great image!
Alan, the phrase is the consequence of an accelerating universe expansion.
Stars at the edge are retreating beyond the edge of the galaxy that light can get to us from.
In effect, they're retreating faster than the speed of light from us. And because that expansion is accelerating, stars closer and closer to us now are reaching that same limit, disappearing from view at some millions of years in the future.
Jeff, a quick back-of-the-envelope calculation has the deviationfrom a flat line for the curvature from the earth at 0.05°
This isn't visible to the human eye over a meter of flat rule.
Imo, you were not looking horizontally at the bar and, rather than measuring the curvature of the earth, you were measuring a fraction of the flst circle the horizon makes over that perspective view.
Paul, you're talking about Olber's Paradox.
Let us not forget: Eratosthenes wasn't just the first human to measure the circumference of the Earth, he first INVENTED GEOMETRY, then he measured.
In my book he is amongst the most brilliant, smartest, highest IQ'd peeps that ever walked the planet.
@Alan (“we’ll never see more of the Universe than we can right now”
I’m not sure what this means.)
The universe is expanding, the Space is expanding. Things are moving out of sight.
Intelligent life in the earlier universe likely saw more of the universe. So when/if we find any of them, we can look at data they collected. =D
Not to be imposing, but does anybody have an answer to my above question?
@Philip
you're questions about curvature are fine. Noone has the answer. If you put it just as "could it be".. then the anwer is yes, it could. Bu we don't know. As far as observations go... it seems that it's a flat universe. Meaning euclidian geometry.
There's probably some crazy (fibonacciesque) ratio consistency in all the stars in the universe to the atoms on earth (given that that specific comparison may even be outside the scope of the massive size suggested). What is it?
Philipp: "Is’t it just as likely that the universe is flat, finite, and ends just beyond the horizon of visibility?"
No.
There are an infinity of numbers but only one zero.
Likewise, the curvature of the universe can be an infinite number of values within a certain bound, but *flat* is an infinitesimally existent one of them, the chances of that are, practically and mathematically, zero.
(Sinza, the difference between our two answers are that I looked at Phillipe's statement of "is it just as likely", the answer to which is an absolute "no".
Our scientists say that Big Bang occured 13.6 billion years ago. Space created is directly related to the lapsed. Our Space may be equal to 13600000000 x 365.225 days x 24 x 60 x60 x 299996.4 KM.
@ Wow
agree, just as likely and end just beyond the horizon... definitely no.
This is an interesting and through provoking blog post, but for me the logic breaks down at the reference to the surface and shape of the universe. It sounds more like the example of observing the ocean curved by atmospheric distortion, than determining a surface triangulation.
Nice information about measuring the globe. Thanks for sharing.
But I was wondering how we can bound the size of universe ?, IMHO we can't figure out the size and shape of the universe.
Note that that "if the universe was infinite, the night would be white" argument assumes that light can propagate an infinite distance. Consider [for example] building a model where light cannot propagate much longer than a dozen billion years.
Well, you could make up any unphysical physical laws to avoid the problem.
But why is light getting too tires to go on after about a dozen light years? What happens to the energy it had? Etc.
The argument for infinite universe originally had also the argument for infinite time. And it was back in the day when the static model universe was a mainstream idea. If you have expansion of space (metric) greater than the speed of light (allowed by GR) you can have infinite universe without Olber's paradox.
The problem is that an infinite universe really requires an infinite time to have existed.
There isn't much of a way around that.
I was thinking of it more in terms that if it's expanding faster than "c", for everything inside it, it's infinite since you can never reach the end. You are limited to below "c", but spacetime isn't.
But Olber's paradox was dealing with the picture of Universe which we now know is not correct.
If the expansion was very very slow in the beginning then the Universe must be much younger than 13b , maybe just 5b years old.
And if the moon were made of cheese, cows would have to be much bigger.
Varde Ljus en enkel förklaring.
Priset utdelas för upptäckten utav att universums expansionshastighet ökar och har nu bekräftas med ett nobelpris i fysik 2011. Genom att studera vita dvärgsolar med en massa som vår egen sol och storlek som vår jord samt med en tvillingsol i ett omlopp kring varandra, så har man upptäckt att en vita dvärgsolen tar materia ifrån tvillingsolen vilket inte är så konstigt då gravitationen på ytan av dvärgsolen är enorm och tvillingsolen har betydligt mindre grepp på sitt egna gasmoln. Jämför jorden med månen som inte har kvar sin atmosfär. När den vita dvärg solen har tagit åt sig en massa och når 1.4 solmassor så exploderar dvärgsolen och blir till en supernova typ Ia. Detta är något som händer väldigt sällan i en galax, en eller två gånger på tusen år.
Men med hjälp att avsöka avlägsna supernovor med hjälp av en CCD laddningskopplad ljuskänslig halvledare detektor. Då man har nått en ljuskänslighet som fångar ca 70 procents av det infallande ljuset, som i jämförelse med fotografisk film som endast fångar 2 procent av det infallande ljuset så har det varit möjligt att redovisa nya resultat.
Genom att kyla ned CCD så sänker man det termiska bruset i halvledarematerialet. Man kan också genom att öppna och stänga slutaren mappar man bort bruset ifrån den verkliga bilden. Genom att använda en bildförstärkare kan man utöka känsligheten så att en enda foton kan registreras.
Genom att scanna stora områden på himlavalvet med hjälp av CCD teknik upptäckte de två teamen ungefär 50 olika supernovor av typ Ia samt att ljusemotionen var lika i alla de olika fallen så kunde man räkna ut distansen till supernovorna och bestämma den accelererande expansionen. Detta hade till följd att den förväntade avstannandet av expansionen på grund av gravitation inte stämde utan att resultatet av accelererande expansionen endast kan förklaras med en 75 % mörk energi och en 20 % mörk materia som finns närvarande någonstans i universum.
En möjlig förklaring kan vara att om man tänder ett ljus och det är det enda som finns i universum i det ögonblicket, så kommer ljuset eller riktigare, den elektromagnetiska vågen som består av fotoner som partiklar eller våg rörelse, att expandera åt alla håll som i en “ballong” som man blåser upp med ljusets hastighet från källan i centrum av ballongen. För en iakttagare som befinner sig i rörelse någonstans mellan centrum och ballongens med ljushastighetens expanderande kant, så är allt som existerar åt andra hållet, ej någonsin är möjligt att upptäcka, på grund av att ljuset inte hinner ikapp sig själv. När våg och foton-ballongen utvidgar sig skapas höjd, bredd, längd och tid i ett icke innan rumsbaserat tomrum, man kan därefter mäta tid och rymd. Detta alternativet står inte i samklang med etablerad fysik, för det finns inte någon fysisk mekanism som tillåter att den elektromagnetiska vågen skapar rumtid på det sättet. Men ändå så påstår jag att det är på det viset. På den plats iakttagaren befinner sig, skapas således ett universum som är en del av den totala “ ballongen”.
Man kan grovt likna vårat universum som en klyfta i en apelsin med 5 % massa.
Lite mindre grovt blir det om man undersöker den bästa kartan hittills av den kosmiska bakgrundsstrålningen, CMB det så kallade ekot av Big Bang. Med hjälp av kartan så visar universum att det inte kan vara samma strålning i alla riktningar. Man hade förväntat sig att bakgrundsstrålningen skulle vara isotrop, utan någon särskild riktning i rymden, men så var det inte.
Om man tittar på symmetri i CMB strålningen så kallas den för octopole ellerr quadrupol och det var ett märklig mönster.Man hade inte förväntat sig något mönster över huvud taget. Men det man såg var allt annat än slumpmässigt det såg ut som en fotboll. Den var octopole och quadrupol komponenter som var placerade i en rak linje över himlen, längs ett slags kosmisk ekvator. Det är ovanligt.
Totalt så finns den stora eftersökta massan i de övriga klyftorna eller fotbollarna.
20 fotbollar formar ett multiuniversum klot där den saknade mörka energin och massan finns. Så kan dessa 19 fotbollar eller 19 klyftor ses som parallella värdar till våran värld i “ballongen”. Vi kan observera effekterna av den mörka energin överallt i universum genom att studera hur stjärnorna rör sig i ytterkanten av en galax eller hur galaxerna rör sig i en galax hop. I båda fallen märker vi att stjärnorna och galaxerna rör sig för fort, det vill säga vi ser att de rör sig snabbare än om de bara påverkas av gravitationen från den synliga materien. Det måste alltså finnas mörk materia som bidrar till det gravitationsfält som påverkar stjärnorna och galaxerna och det finns i samtliga “klyftor eller fotbollar”.
Nu kommer det riktigt paradoxala i den här upptäckten. Gravitationens påverkan på expansionen förändras inte så mycket med tiden, utan det är gravitationens i stort sett konstanta påverkan som leder till att universums expansion accelererar. Hur går detta till? Jo, enligt Einsteins allmänna relativitetsteori är det energidensiteten, rho, och trycket, p som tillsammans utgör källan till gravitationen genom sambandet rho + 3p. I de flesta sammanhang som vi är vana vid är trycket försumbart litet jämfört med energidensiteten, men för mörk energi är p = – rho i det enklaste fallet, så trycket är inte bara negativt (däremot kan energidensiteten aldrig vara negativ) utan så negativt att rho + 3p blir negativt, och då blir gravitationen repellerande och vi får en accelererande expansion. Dessutom är det så att i det enklaste fallet, som jag visar ovan, så fylls det på med ny mörk energi i det nya rummet som bildas allt eftersom universum expanderar, så den blir aldrig ens förtunnad!
Saknar Ariel Goobar och Carl Pennypacke vid nobelprisutnämningen i fysik 2011
Bra länk: http://news.bbc.co.uk/2/hi/science/nature/2814947.stm
http://www.youtube.com/watch?v=p7T5i7CS1CY&feature=youtu.be
Universum skapas när den elektromagnetiska vågen expanderar med ljushastigheten. Då kan man lägga i den bubblan en tumstock och mäta höjd längd och bredd samt tid.Vågen skapar rummet och tiden i ett icke rum eller i ett ingenting. Stick hål på bubblan och dra ut universum ur punkten. Man vränger universum ut och in så att bakgrundsstrålningen blir en mittpunkt i stället för våran vintergata. För åt vilket håll vi nu än tittar så är det start punkten som vi ser i ett krökt universum. Då är vi 13 milj. ljusår ifrån startpunkten. Den strålningen som har gått åt andra håll skapar sina egna universum skilda från oss därför att dess ljus aldrig når oss någonsin. Men massa finns ju i dessa universum och påverkar vårat universum. Kan man kalla den massan för den saknade svarta massan? Universum är det vi ser och iakttager, men så mycket mera finns utanför denna iakttagna horisont.
Space as in the space between planets and stars, empty space that is, is nothing. If it is nothing, how can it end? It is obvious to me. it can't, end of. Just like there was no begining to time. "Everything started with a big bang", So what happened before that? There are some things in life you just have to accept. I live in a world almost full of morons, who believe in gods, I just have to accept it, I can't change it, there is no hope for these people,
well we can calculate the radius of universe, where the furthest particle of light is by calculating the age of universe and speed of light
"“Everything started with a big bang”, So what happened before that?"
Nothing.
And since you already alluded to the idea that nothing has a start or an end, the end of nothing is where the universe begins.
No No No, I said how can nothing have an end? And you are assuming nothing happened or existed before the big bang. Assuming I say again! What caused the big bang just appeared by magic, did it?
When something turns up then there is no longer nothing there.
Really, you aren't even getting this?
"What caused the big bang just appeared by magic, did it?"
That's what christians think happened.
very interesting article.
I have two questions, if you have any free time.
why should the apparent size of the hot spot be 1 degree in order for the universe to be flat?
second ,why the light rays emitted from the opposite sides of the hot spot are not parallel? isn' it true that light rays from distant objects are parallel?
in the case of flatness is it true that each of the other 2 angles shouldbe 89,5 degrees which means that rays are almost parallel?
let me correct you and say you can leasure earth curvature from a mountain.
Al Biruni did it
http://en.wikipedia.org/wiki/File:Abu_Reyhan_Biruni-Earth_Circumference…
that the problem of todays history of science
it always jumps from greeks to renaissance europe
science droped heliocentrism
and now ethnocentrism yet it didn't drop eurocentrism
or maybe the universe is as small as a pen dot and everything is in it. ? and the things we see around us are trillions times smaller than a pen dot. ?
excuse my English
Gagan, that is impossible and meaningless. Think about it: What are you saying the universe is small relative to? An actual pen dot you make on the paper? Well that pen dot is clearly vastly smaller than the universe.
So rather you're supposing that the whole universe is actually much smaller than we think it is, but we are also proportionally smaller? Well then the universe is exactly as big as we think it is, in the units we are using, which are "smaller" than we think they are, relative to... something?
It's all relative. Sure there's some scale at which our universe, or at least the observable universe, can be considered tiny. Our planet is tiny on the scale of the galaxy, much more so the universe, but large to us standing on it. Yet also exactly the size that it is in the units we use to measure. Imagine the universe is bigger or smaller and the relative sizes of everything doesn't change. Light still takes billions of years to cross the universe.
@ SLDUA (Noida)
That is true if the Universe has expanded at light speed all the way from its inception. However calculated regression from observed relative expansion rates over the available time imply that the Universe was quite a bit bigger than it should have been at the beginning. "Inflation" was proposed to deal with that discrepancy - a nebulous notion that the Universe underwent superluminal expansion before the rules changed to stop it. It was pulled out of somebodies arse some time ago and it's still part of the standard model. It depends on quantum jiggery pokery and seems to explain things well while still being totally mysterious to those not versed in quantum magic. So the Universe is bigger than a simple light speed calculation would imply.
@ Chris Payne
"Space is nothing" is a classical concept that quantum boffins disagree with. See Lawrence Krauss.
Whether "quantum space" is part and parcel of the product of the Big Bang and so constrained by expanding space or part of the infinite void that one assumes space is expanding into is just another thing I don't know. :)
The universe is unpredicted and is a mass elusion of our physical reactions say a ball what is the 4th of what it holds and times that by its radiants and the universe doesnt gave that its what God made it but certainly if there aint life on other planets then how is it comfirmed tobe infinitely big if it is then there is life such as et extra terrestrial is in our path ancient manufactures are real of aliens then God is an alien of the universe yes it all adds up to this if the universe is infinite then theres at tobe life and if thats true gods an alien trying to save us or destroy what he has made scientist say that if we arent alone whos out there and just listen about how smart the goverment think they are they are holding what we need we all ready got our answers of the universe its just tomany questions but just wait soon to he captured life is eternal so make your mark hell or heaven you choose or is it in the universe spiritually? And our biggest question when were and how is this gonna happen you tell me ?????????
Our universe is just a dust partical and there is mqny other particals out there I am saying that in our universe is us on earth a partical is just another universe and in that universe another partical is another universe its genius and all you see is a dust in another dust they are all what we are thats why we are made of dust cause we are dust the universe is dust so a dust particals that nobody saw ta
his but only a poor portion knows this like when somebody moves they create somebody elses universe we got bigger though but thats the universe it is what it is
You can say that.
Nobody has a clue why.
I've never discussed my experience before so here I go.Whilst having dental surgery as a 8 year old child I experienced the begining of the universe,bear with me please.Whilst under the effects of the anesthesia I saw in my mind two steel balls exactly one inch in dia .banging repeatedly together going faster and faster,about one trillionth of a second before they exploded every thing went blank and I heard someone laughing in a teasing way.One year later same dentist similar surgery the exact same thing happened ending in the same teasing mocking manner.As an 8 year old child I had no concept of the universe, why these images came into my mind is unfathomable.My theory as a 9 year old that every time these balls collided they formed a universe many many times over. Now I'm into my latter sixties it often crosses my mind, what the hell happened?I believe to this day somehow I was privy to the start of our universes,even back then I knew there was something like multiple universes existing on other planes.Did I illusionate? probably,but I was so close in my mind to the BIGBANG as they now call it.When I was still very young I always though it was God teasing me.I don't knew if I feel better or just embarressed about my revelation.
Your brain does weird things when it's being shut down.
Nothing more than that.
The WMAP picture says it shows fluctuations of the entire sky, but how big is the entire sky in terms of degrees^2 ?
I am studding in school and we have to answer a question. I have a few questions about the Universe
1. How big do you think the Universe is?
2.Why do you think its that big?
3.How old do you think the Universe is?
4.How do you know the Universe is real?
5.What else do you know about the Universe?
Wow. People have been following this post for nearly a year! Great comments and observations by all! Really makes one think. What the universe is, I believe, is the three-dimensional surface of a four-dimensional hypersphere (that hypersphere part being the cause of all the expansion). That fourth dimension, while imperceivable to us, is still perpindicular to the other three dimensions, and is still subject to the same Euclidean geometry as the three dimensions we know. If we use the same algorithm as we do here on our home planet (we can see about 16 miles to the horizon on a sphere with a circumference of about 24,000 miles) then it is not hard to infer that if we can see about 47 billion light years to the universal horizon, then the circumference of the universe must be about 70.5 trillion light years with a diameter of about 22 trillion light years and a surface area of approximately 158 quadrillion square light years (all applicable to the fourth dimension, so not necessarily equivalent to what we would measure here in our three). I'm sure that my math is off somewhere, but Ethan is right. Even if it is closer to the 14 trillion light years in diameter that he postulated, the tiny portion of the universe that we can observe would appear completely flat to us with our limited means of measuring it. By either of our calculations, the universe is at least millions of times larger than the part we can see.
Do not get locked into thinking as a three-dimensional being, looking from the center of a balloon 47 billion light years in all directions, not being able to see beyond that, and thinking that that must be all there is. In the hypersphere, the horizon curves away from you no matter which direction you look, thanks to that pesky fourth dimension, so no matter which direction you travel, even as new galaxies appear before you, the galaxies behind you will disappear and you will always feel as though the universe is 47 billion light years in all directions.
Obviously, as the universe ages, the hypersphere will grow bigger and bigger (as will our observable universe), and the universe will appear to be getting flatter and flatter, though it will never EVER be truly flat. Weird thing is that yes, we know that if we take off on a straight-line journey here on the two-dimensional surface of our sphere, we are getting farther away from our point of departure and closer to it at the same time, and eventually we will reach and pass the point at which we departed. Repeating universe and all. Seems to work basically the same in the hypersphere, farther from and closer to at the same time, but without ever being able to reach the same point, closer and closer, infinitely closer but never actually reaching. I'd like to know the math involved in that if anyone has an idea (college calculus I was as far as I got, so don't get too technical if at all possible).
vol the surface of a sphere contains 720 solid degrees of angle.
This is basic geometry.
Thanks for the trig/geo lesson, Wow. Nothing whatsoever to do with my question, but I'm sure someone somewhere will find it useful.
Sorry, Wow, thought you were talking to me.
Didn't see vol above me, my sincerest apologies.
no worries. the handle confuses conversations.
Interesting thinking Jay, the extra dimensions thought isn't new, just not possible to prove. I would be more interested how you explain accelerated expansion with 4th spatial dimension??
There's nothing that says there won't have advances in science so that someday we will find a way to observe dark matter and the rest of the universe.
drhouse,
I would agree with your first assertion, but not your second (unless our understanding of physics changes in a HUGE way). GR tells us we cannot observe events outside of our light cone. It's a principle of physics that we cannot ever observe the entire universe.
Take a bowl from cupboard and place on table. There is nothing in it.
Now make something from nothing.. Impossible
So there had to be "something" to have made the BB..
Interesting comments so I shall sleep well ..
The hubris of man has always been consensus based on assumptions and I am right now pointing out a big one.
There is a current scientific consensus that black holes must preserve physical information in their horizons somehow. "Physical information" referring to quantum determinism and reversibility in the form of the quantum evolution operators via some as yet undiscovered form of quantum gravity.
Now, even without a formal theory of quantum gravity, there is a huge problem even if we did have one... If black holes preserve information in their horizons it would be in a constant state of change. Material is constantly being added to a black hole so the horizon would always be preserving new physical information over time. Meaning all black hole horizons are utterly unique entities based on the black holes mass.
In this case there are 2 possibilities with regard to theoretical black hole coalescence events or mergers. One, we must discover a way to describe quantum gravity then use that theory to mathematically explain how the constantly changing horizons of 2 black holes can scramble unique physical information preserved in their respective horizons and some how sort it out later after they merge... Which I think is utterly irrational and impossible thereby calling it the "Black Hole Merger Paradox" or "Black Hole Merger Problem" if you will.
OR
Black Holes can never merge. Binary black holes must synthesize each other by an unknown method to preserve their unique quantum evolution operators preserved in their horizons. Singulosynthesis: Is a deterministic process by which binary black holes must fail based on their mass to preserve the physical information in their unique horizons at the expense of time. What might failing black holes synthesize you might ask? Well... what elements on the periodic table have no definitive method for creating them? Big hint incoming... the first 4.
So hang on just a second... If this implies how the universe began... How can we reconstruct and mathematically describe a process that created the universe? Black hole mergers still occur thankfully, albeit on a less frequent basis. This event is on the very edge of our perception right now. We must observe some unique patterns in gravitational waves, I have four in mind right now. They are unique in the sense that nobody has thought of them and therefore nobody is looking for them. Once these unique generic patterns can be located, we can focus our observations at pinning down the true signature of a failing black hole precisely. This will reveal the mass loss rate of a failing black hole.
With that information in hand we can then simulate the true sub Planck environment of a black hole, establish a quantum theory of relativity, amend the second law of thermal dynamics, and figure out a great deal more. Otherwise the universe is inherently irrational.
Unfortunately, Houston has a problem. Right now gravitational interferometers are using exact predetermined theoretic gravitational wave signatures to hunt for patterns in the observed data. Patterns based on the assumption that black holes do indeed coalesce. My idea requires the opposite method to be detected.
The gravitational waves I seek must be observed then quantified. However all may be good... if I am right, black holes will likely be found using the predetermined theoretical signature method. If they are found, I predict they will deviate from their expected behavior drastically at some point. It will be important to not loose track of them when they do.
@ Jimmy
please take your theories somewhere else. This topic isn't about that. It's about the size of universe. Not your daydreams about what should and shouldn't be calculated in black hole quantum gravity....
"The hubris of man has always been consensus based on assumptions and I am right now pointing out a big one."
No, you're DEMONSTRATING one.
And overwhelming hubris at that: YOU are the one special person who, unlike all those "eggheads" who you leave unnamed so their identity and ACTUAL statements cannot be found and compared to your description of them, has not succumbed to this hubris and can clearly see where EVERYONE ELSE has it wrong.
"Take a bowl from cupboard and place on table. There is nothing in it."
And after that impossible thing, go to Milliways!
There is not nothing in it. We've never found anywhere where nothing exists.
Take your bowl: it has space in the middle. That's not nothing. It has photons you can see emanating from the surface (otherwise you would be unable to see it). That's not nothing.
So go ahead, YOU get a bowl of nothing.
Let us know what happens next.
TIA.
I want aliens to come and show them selves, or land with big UFOs, not violently but just show themselves to us, make us understand how incredibly small we are in comparison and that there will be no help from the outside if our Earth collapses, either of environmental purposes och economically.
what comes after our humankind that we know of? when we dissapear, will someone, something ever know about about the species called humans, that lived here a long time ago?
Why can scientists be able to 'know' the age of the universe with precision, say 13.75 billion years old, but fail to know the size of it?
@Indro #113: Because we learn things about the Universe by _observation_. We know pretty well how big the giant sphere is from which light has had time (13.75 billion years) to reach us. But we cannot know with certainty what is outside that sphere, because light from farther away hasn't had time to reach us yet! In another billion years, that sphere will have gotten bigger, and we'll know more.
Ignorant space dreamer here. If our universe is 14 billion years old. Then how do we see light from galaxies 50 billion light years away?
If anything, the CMB and WMAP info reveals that we live in a nebula. All but one kind of nebula (and probably even that singular example) came from an exploded Star. We have never witnessed a singularity: they are mathematical constructs which cannot exist except in our imaginations. Instead, our Universe was once a massive Star, just as most of our Galaxies once were. It is believed that these massive structures cannot exist for long under the weight of their own gravity, but that may not be the case.
So when we discuss the size of our Universe, we are really discussing the size of our NEBULA. The "Heeck" limit of the initial light from the Big Bang can only be 1 quintillion years in any direction from the center of the event (since this is how long photons can live in an unimpeded environment), so we are initially looking at a positively curved bubble with diametric points separated by 2 quintillion years.
Light travels about 10 trillion kilometers or 6 trillion miles in one Julian year of 365.25 days of 86,400 SI seconds each. I don’t have a calculator that powerful, but off the top of my head, 1 trillion (10^12) goes into 1 quintillion (10^18) 1 million times. 10 trillion (10^13) times 1 quintillion (10^12) equals 1.0 X (10^31) trillion kilometers or 6.0 X (10^30) trillion miles.
Since we live in a Euclidian Universe this light traveled diametrically in all directions away from the initial “Big Bang”, we have a diametric “Heeck” limit for the original non-Superluminal light. This limit is an intrinsic index of spherical harmonics consisting of a 2 quintillion year bubble about 12.0 X (10^30) trillion miles or 2.0 X (10^31) trillion kilometers in diameter, and that is for the initial “Heeck” Limit of light.
Of course, light propagates more light since it decays into lower spectra. This is essentially what happens to the photons from your light bulb in a closed room: they bounce off the walls billions of times and then decay into infrared energy, which is to say the visible photons are now infrared photons, which will continue to decay. In fact, every "photon" of visible light is only visible because it is constantly shedding smaller infrared photons. Anybody who says otherwise doesn't understand what a photon is. At 186k mi/sec speed of light X the estimated 15 billion year age of the Universe (rounding up from the CMB estimate of 13.7 billion years), we might have a Universe around 68 sextillion miles wide. It is certainly not “infinite” as is often assumed!
Now. When we use these kinds of numbers we are ONLY discussing how big the Universe is if visible light expanded at a constant rate. Which it doesn't. We can slow light down in an Bose-Einstein condensate, we can slow it down in certain crystals and manifolds, and we can speed it up much faster than its normal speed. The speed of light is mutable. When astrophysicists say that the Universe rapidly "inflated" or expanded, they are saying that the SPACE grew much FASTER than the normal speed of light. This is why we must discuss the initial expansion in terms of Superluminal light.
The best way to wrap your mind around the issue is to accept that all spectra on the electromagnetic scale consist of photons. Gamma "Rays" are actually Gamma-Ray PHOTONS. Hard and Soft X-Rays are actually X-Ray PHOTONS. Extreme and Near Ultraviolet light (including our very small Visible spectrum) is actually Ultraviolet PHOTONS. Infrared, Terahertz and Microwave radiation is all PHOTONS. All of the Radio-Wave Spectra from EHF to ELF are actually Radio PHOTONS.
Below the Radio spectrum light probably decays into matter. I say this because "Pair Production" actually informs us that a photon, in this case (usually) a Gamma-Ray photon, actually consists of an electron and a positron, which means the electron has a monopole-tail at the end of which forms an anti-electron aka a "virtual particle" and these two nodes oscillate around each other incredibly fast. The highest speed cameras we have invented have actually taken pictures of photons and revealed that they are rolling explosions with magnetic lobes (seems there are two or four). In Pair Production when a photon with a specific energy slams into a specific metal with a proton it can spare, we see the spallation of the photon into its constituent matter. We didn't "create" matter from energy, we simply revealed that all photons are energized matter moving very fast.
What this means is that at the bottom of the electromagnetic spectrum, below the Radio slot, we can place MATTER, which of course (Bob) is comprised of three orders. This means we have three more domains of electromagnetic spectra below the Radio photon.
At the core of all Matter is probably the unassuming neutrino. Which is interesting, because theories on Superluminal light involve neutrinos. And high speed footage of photons in a tube show that there is a "ghost" photon that precedes the actual photon, but slightly faster, which seems to be a Superluminal neutrino twin. It should be pointed out that Superluminal isn't a set speed, its just any speed faster than the accepted speed of light.
Eventually the light from the Big Bang will decay, and slow, and decay, and slow some more, until it is just a bunch of neutrinos. Conceivably they reach apoapsis, and I say this because (listen closely) ALL PHOTONS ARE IN A BALLISTIC ORBIT around their point of origin. They are piece of matter gravitmetrically bound to their source. This is why our satellites leaving the Solar System are slowing down at the same basic rate that we see light Red-Shift as we look in all directions: the two maths are exactly the same.
The light from the initial Big Bang will slow down and turn into neutrinos, which is why everywhere we look in the Universe we see a neutrino condensate tugging at everything traveling through it: i.e. creating "gravity".
What is alarming about this is that a Big Bang might very well be followed by a Big Crunch. In any case, those astrophysicists who claim they have measured a vestigial revolution of the Universe should probably be moved to the front of the class. We live in a SPHERICAL Universe which most likely resembles a spiral Galaxy with a central bulge, a "disc" consisting of trillions but a limited amount of Galaxies and Stars, and a finite edge. I have no idea why Einstein thought that light reaching the edge of the Universe would "curve". That is ludicrous! Does light "curve" when it reaches the edge of a Galaxy? NO! Are Galaxies "flat"? NO! We live in a Euclidian Universe, with depth and breadth and finite edges. Beyond the edge of our NEBULA we can expect to find, as Hawking once postulated, a large dimension in which particles are popping into and out of existence for very brief periods of time (like at the edge of a Black Hole aka a Neutron Star), only at some places you have denser particle articulation and thus micro-gravity which encourages gravity waves, causing a collapse of virtual particles into the stuff that makes... other... Universes.
So what if we have to use the word "Cosmos" to designate the larger domain? Once upon a time the Greeks called our Galaxy as the sole limits of the Universe and we had to accept that they were wrong. We live in a Multiverse. The gravity waves from the creation of our own Nebula, i.e. the explosion of our original massive Sun, probably created sister-Universes, so we can expect to find that we live in a small "Cloud" of Universes. Beyond this, we live in an infinite Cosmos with uncountable numbers of Universes.
As Sagan said: "it's turtles all the way down".
The opening quotation is worth repeating just because everybody tends to quote something and promptly forget it.
"“The greatest enemy of knowledge is not ignorance, it is the illusion of knowledge.” -Stephen Hawking"
I'm not sure we could designate which enemy is greatest. There are lots of candidates for that title. Let's consider the assumption. We notice a red shift in light from galaxies and we *assume* that it's caused by Doppler shift. We see resemblances among stars and we *assume* whole libraries of information from such observations. We *assume* that stars are powered by fusion because that is the only thing we have been able to think of. Nobody but nobody ever examines their basic assumptions. If those assumptions are wrong then most of what we think we know about the universe ain't so. Then we run into another candidate for "greatest enemy": scientists usually would rather be wrong than uncertain. And to top it off, when somebody points out these discrepancies, they say *he* is crazy!
Here is another quote that seems to apply to this topic: "We have met the enemy and he is us." - Pogo
Using the best data available (Planck: Omega Knot of 1.02 +/-.02), the universe is 266 bly in diameter. Our observable universe would be represented as a disc on the surface of this sphere, the disc having a radios of 46 bly. There is actually a detailed explanation and diagrams showing this curved model on the flat universe society website.
Ok so tell me if I got it right.
Distance (radius) of observable universe is now about 46.6 billion light years.
If universe is actually curved, it must be at least 14 trillion light years in diameter for it to seem flat at scale we measure?
Is above correct? Thank you people.
@Justin #120: Basically, that is correct. I believe that "14 trillion number" would correspond to the length of a "great circle" path or "circumference" that passes through the whole universe and returns to its starting point in space (*NOT* a path in the travel sense, but rather just a reference line).
The "radius of curvature" does not correspond to a radius of our _view_ through the universe. If you need a picture analogy, you'd need to use an embedding diagram, where the Universe is a gigantic balloon (and what we can see is a small patch on that balloon), where the balloon curves in some ficticious external dimension.
Yeah, I know this doesn't help. Sorry.
One way to consider it is an analogy of a travelling walkway, just like you get in airports.
How far is it from one end to the other? Well there's the linear distance and you can see that from the outside pretty easily.
Then again, there's the distance you have to walk TO GET TO THE OTHER SIDE. And that's a lot shorter. Because as you travel the moving path, it moves too, changing the distance by you in ways that depend on how you move.
So a lot of nomenclature of "size" or "radius" or whatever is done in a similar bipolar way: If you were to travel "now" (as we see it) and the universe is held static, or the distance you'd travel *if you set off now*, usually as a photon, but that again is taken *externally* since from the frame of reference of the photon, every answer would be "No distance", which is a little unhelpful.
Based on the diameter of the universe being at least 14 trillion light years, that means the average expansion speed of the universe must have been at least 1,000 times the speed of light since the big bang around 13.7 billion years ago.
I wonder how this minimum average expansion speed compares to the speed calculated for the initial inflation that may have occurred at the beginning of the big bang?
that is really interesting
As a lay person I have enjoyed reading this article and comments but it does seem that astro physicists have to turn a blind eye to the laws of physics and invent new hypothesis to support the Big Bang Theory.
First the universe needs to expand at 1000 times the speed of light which requires a new theory (inflation) to justify then it has to slow down to c to comply with more conventional laws, then it has to speed up again as the more distant galaxies appear to be moving away faster than they should be plus the universe is larger than it should be based upon an age of 13.8 billion years which introduces the need for additional forces such as dark energy and dark matter.
I can just imagine the Flat Earth Society putting forward similar arguments to support their theories.
Is it possible that instead of The Big Bang there is The Big Volcano? A cosmic volcano at the centre of the universe which spews out a new universe every billion years or so. Our universe would be like a bubble with a 14 billion light year radius inside which you would have concentric bubbles with radius of 13 billion 12 billion etc and looking outward we would be inside larger universes.
The reason the universe appears to be larger than it should be is because it would be older than we think. Maybe 1000 times older.
The reason distant galaxies appear to be moving away at an accelerating rate is because they are not on the same circumference as us they are at a much greater radius on a larger circumference. This would account for the redshift and relative velocities.
Universes would travel through space like ripples on a pond. We would be on the 14th ripple but there could be hundreds or thousands of ripples. It may even be that the cosmic volcano sucks matter in at the bottom from old collapsed universes and blows it out the top as new universes like a convector heater which would provide an alternative explanation for dark matter and energy.
I don't have any evidence to support my Big Volcano Theory and it is only one possible explanation amongst many. It just seems that scientists go to great lengths to explain things which don't seem probable in order to justify current beliefs.
For thousands of years we didn't have the Big Bang Theory and astronomers were more open to alternative ideas. Now it's like we have boxed ourselves into a corner with a theory that has to be supported at all costs despite gaps in the logic and evidence to the contrary.
First the universe needs to expand at 1000 times the speed of light which requires a new theory (inflation)
Well your problems are you're writing a story, that is the first part, and that story is written post-hoc, therefore applies intent to follow that story when the story is entirely your invention.
Your other problem here is that your claim here is wrong. Inflation explains why we're in such a nearly perfectly flat universe.
Given your story is your creation, and that story starts off wrong, the problem isn't with the science, it's with you.
Claiming this is why is not showing why. Your claim, on the face of it, is silly. That does not have the effect you claim. Prove what you mean, since either your wording is incorrect or your claim is.
And no theory either. Just a wild assed guess, a fiction you've created on happenstance.
That's my theory on it.
And this one, unlike yours, has some evidence for it.
"Is it possible that instead of The Big Bang there is The Big Volcano?"
No.
Because when the photon we're seeing left that object that object was less than 50 billion light years away.
“Is it possible that instead of The Big Bang there is The Big Volcano?”
No.
Well at least you confirmed my theory that Big Bang Theorists are not open to alternative ideas. Thank you.
So what do we reckon? Was that a spam attempt, to test the anti-bot software, or just a fucked up PC with an unnoticed spambot gone do-lally?
Or is it trying to get someone to click on the link to the user and get infected by a spambot gone do-lally?
Something to keep in mind (a careful search and NOT linking to any actual site) shows this is from a "company" that says it's in Russia.
So definitely a botnet creation tool
"Well at least you confirmed my theory that Big Bang Theorists are not open to alternative ideas."
Oh, we're open to ideas, dearie. Just not any old idea. There has to be something at least *vaguely* rational about the "idea". Otherwise it's not an idea, is it. It's rambling. No evidence of thought.
how do we know there is an end to the universe it could be like we are just shooting an arrow at a wall and we just jump on the next wall and shoot another arrow in an never ending cycle and we just think there's an end because of our brains thinking there's a reason for everything you never know because our species will go extinct before we will ever find out but there's no reason to not try and find the reason to existence so good luck to you guys trying to find the meaning to life.
"how do we know there is an end to the universe"
We don't.
The "end of the universe", though, is the size of the universe that came from the big bang. And there's no indication that it inflated fast enough to be infinite in size in the finite time that has passed since then.
So it's a pretty solid logical chain there.
Not sure what you were trying to say with the rest of it (the majority of the post).
But there is a reason for everything. Even if that reason is "It was able to happen" (like, for example, radioactive decay. Any decay event appears to have no direct even causing it to decay at that time. Only the opportunity for it to happen, then let time pass).
What there isn't is a humanistic storytale reason for everything. The radioactive decay doesn't happen because it "decides" to decay. It doesn't happen because some pixie got round to making it happen.
"Shit happens" is a reason. It's not one we like, so we make up a story reason. "The world is against me" or "I have bad luck" or "It's so perfect, it must be designed!".
And frequently (and this is a problem in science as well, reductionism is necessary and damn useful, but it does lead astray on occasion if you stick to it too much) there's not a single causal chain leading to the event. It's a mish-mash of priors of multiple self-prior causes that make no "sense" in a story, so we simplify it to something we can follow.
It's better to think of those as "part of the reason".
Interesting story abour size of universe I think our calculation about size of universe is wrong we will find out the other way to calculate the size of anything which is applicable to any size and shape of any object and I also think that beyond this universe there is only white light. I am trying to research on this well it goes to hundred of years but I want to give something to about the secret of universe in my life .
"Interesting story abour size of universe I think our calculation about size of universe is wrong"
Why? Just so you can be different? Because there doesn't appear to by ANY "reason" for your belief. Just your desire to say it.
Maybe the light you see is your esophagus...
I was totally stunned, dismayed, and deeply disturbed by the recent discovery on YouTube of dozens and dozens of video postings and so-called "documentaries" pertaining to widespread modern-day belief in a flat Earth with a dome of stars and other celestial objects! Also A LOT of NASA moon landing conspiracy videos and other nonsense. These videos have hundreds of followers and posts that support this garbage.
If the Universe indeed has a shape like a sphere, then what is "outside" of the Universe? If you say "it is nothing", then what's "outside" the Universe is just unbounded/infinite space as space is that which has no shape (nothing).