"Where you used to be, there is a hole in the world, which I find myself constantly walking around in the daytime, and falling in at night." -Edna St. Vincent Millay
I'm sure you've thought about it before: what would happen if you dropped something into a bottomless pit?
No, not one of those fake bottomless pits that you find in various Mystery Spots off the beaten trail.
 Image credit: Mel's Hole, courtesy of http://komonews.com/ in Seattle, Washington.
Image credit: Mel's Hole, courtesy of http://komonews.com/ in Seattle, Washington.
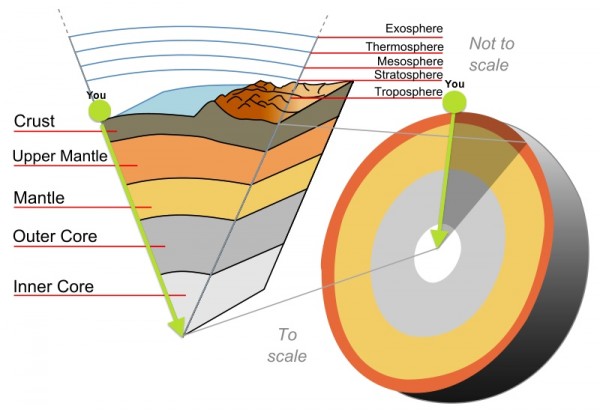
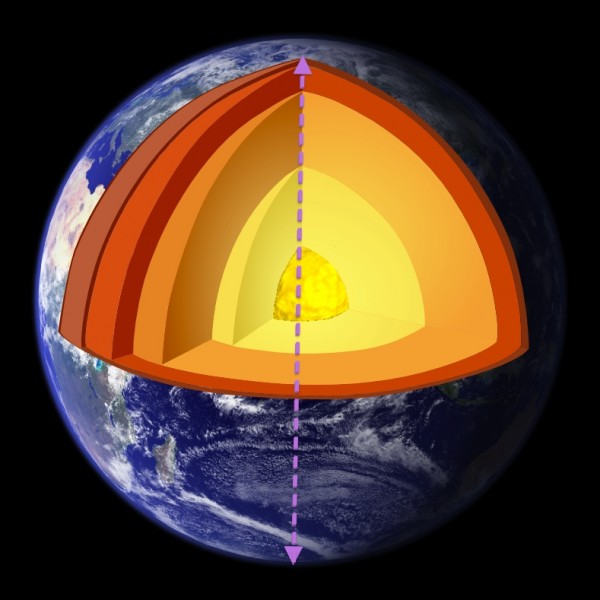
Those may be deep, but they're definitely not bottomless. And I want something truly bottomless. To get that, we'd have to use our imagination, and pretend there were somehow a cylindrical shaft that extended all the way down, past the Earth's crust, mantle, and inner and outer cores, all the way to the center of the Earth, and then that continued back out to the other side, most probably into the ocean if you live on a continent. (These are known as antipodal points.)
So, despite the pressure and temperature gradients all the way down, despite having a liquid, molten outer core and a radioactive nickel-iron-cobalt inner core at over 4000 °F, let's assume you've created something that will stabilize your cylindrical shaft, creating a true bottomless pit.
(Maybe a graphene cylinder of sufficient thickness that's cooled by a layer of liquid helium pumped through it would do the trick?)
So, now we're good, right? We've got a bottomless pit that starts at one point on the Earth, goes all the way through the center, and back out the other side.
Are you ready to dive in?
Here goes your master plan to make the world's longest skydive look like a paltry coin-toss. While Felix Baumgartner may have journeyed 36 kilometers, your plan is to go more than 12,000 km, all the way from one side of the Earth to the other, through a true bottomless pit!
Well, it turns out your brilliant plan wouldn't get you very far. Here, near the surface of the Earth, the atmosphere is moving along with you and the Earth's surface as the planet rotates, at a clip of about 1000 kilometers-per-hour, with variations depending on your latitude.
This isn't a big deal for most normal applications, but as you start moving away from the surface of the Earth's crust and deep into the interior, you'll find that, horizontally, you're moving too quickly.
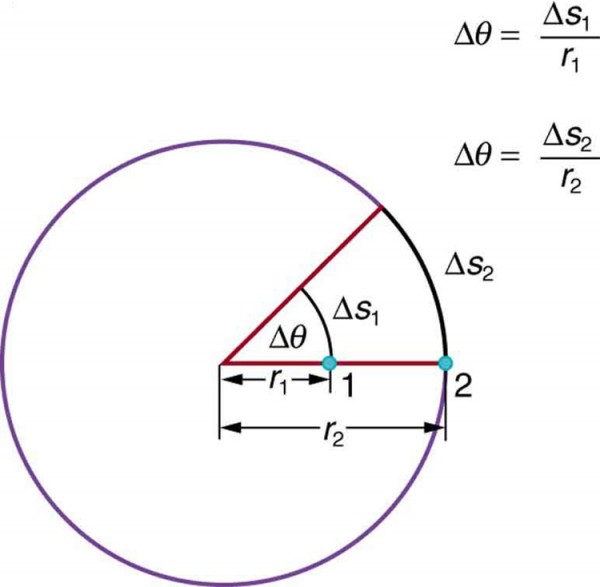 Image credit: OSC Physics Maintainer of http://cnx.org/.
Image credit: OSC Physics Maintainer of http://cnx.org/.
It's only a matter of time (and, surprisingly, a few dozen kilometers) before you find that you've smashed into the wall of your cylindrical tube, since the Earth is still rotating -- with the interior rotating more slowly than the surface -- after you jump!
There's a fix for this, though.
Build your shaft directly along the Earth's rotation axis, from the North Pole through the center of the Earth all the way out at the South Pole. Now, there will be no effects from differential rotation, no coriolis forces, and -- so long as your cylindrical tube holds -- nothing keeping you from having a true-to-life bottomless pit!
So do it -- jump into the bottomless pit -- and what happens?
Now, the fun begins! You start accelerating downwards as the air rushes by. Pretty quickly -- after about 7 seconds -- you hit terminal velocity, which is about 140-to-210 miles-per-hour, depending on how your arms and legs are positioned. This speed actually increases marginally for a while as you continue down the shaft, as the inner layers of the Earth are denser than the outer layers.
Unfortunately, because there's air in this cylindrical shaft, it will take you somewhere around 20 hours to reach the Earth's center: a journey of around 4,000 miles (or 6,400 km). When you do, you'll be moving at a paltry speed of around 300 miles-per-hour (or 480 km/h; your actual number will vary dependent on air density in the core of the shaft), and you'll only overshoot the true gravitational center by less than 100 miles.
In other words, in fairly short order, you'll be trapped in the gravitational center of the Earth, a crummy fate for anyone or anything tossed into your bottomless pit.
 Image credit: X-Fire's Palsonite Cylinder SET VC/ Type96 http://www.x-fire.org/.
Image credit: X-Fire's Palsonite Cylinder SET VC/ Type96 http://www.x-fire.org/.
So this time, you'll be ready. Your cylindrical shaft, reinforced and cooled, will extend continuously from the North Pole to the South Pole, and you'll have removed all the air from it!
Now, the fun begins. You toss an object into the bottomless pit, and what happens?
It never reaches terminal velocity! On the contrary, it just keeps on accelerating, reaching a maximum speed at the very center-of-Earth of over 11,000 meters-per-second, which is around 40,000 km/hr or 25,000 mph! Your journey to the center of the Earth only takes about 22 minutes, with some uncertainties in there based on the densities of different layers, but because there's no air resistance, no energy is lost, and that's where the fun begins!
"I wonder if I shall fall right through the earth!" -Alice, from Lewis Carroll's Alice In Wonderland
You'd now slow down as you progressively moved away from the Earth's core and through the various outer layers; your acceleration would change as you moved as well, dependent on the total mass enclosed by a sphere of your current distance from the Earth's center, as well as that distance (squared) itself. And a total of 45 minutes or so after you were dropped into the shaft from by the North Pole, you'd emerge from the South Pole.
Only, because the South Pole's at an elevation of around 2,800 meters (over 9,000 feet), you'd barely be able to see daylight overhead before you came to a halt, and then had the identical journey back from whence you came.
And so you'd make a round-trip, back through all the various layers of mantle, outer core, and inner core, to the center of the Earth, and back once again through the northern layers. About an hour-and-a-half from when you first were dropped in at the North Pole, you'd re-emerge at the same exact position you started at.
And you thought it would be fun to travel through the chunnel? Well, now you know what would happen on the Earthly adventure of a lifetime.
And that's the physics of a bottomless pit!




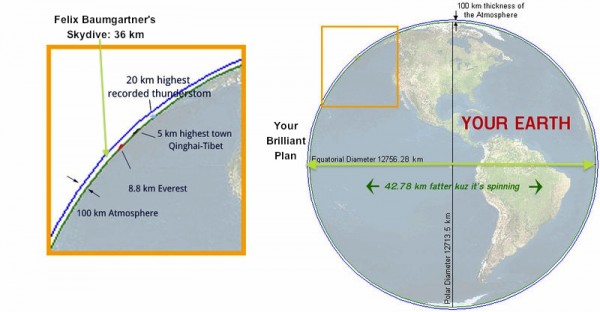



Cool. Also, no matter what angle the tunnel goes through the Earth, it always takes the same amount of time (40-odd minutes) to fall end-to-end.
same amount of time as a surface orbit would be.
The secret to not having a boring trip with no payoff is to start at the south pole, then you'll make it all the way to the surface at the north pole (and out into the air?)
Im sorry to destroy your dreams.. but.. there are still more effects that you didn't account for.
First, there is the gravity of the moon. Due to the rotation of the moon around the earth, the gravitational centre of the earth-moon system changes over time w.r.t. the centre of the earth. Because your shaft is at rest w.r.t. the centre of the earth, you would still smash into the walls of your shaft.
Than there is the precession of the earth due to the inclination of the moon and earth, changing the orientation of the rotation axis of earth. You might think thats a minor effect but it is not (if my calculations are correct). We have a precession period of roughly 26000 years. In that time the rotation axis draws a circle at the north pole with a radius of about 1000km. In 45 minutes, this translates to a movement of 1.3m. Now, when you start your fall, you will have that velocity, bout you do not make the rotational movement. After some trips, you would smash into the wall because you didnt account for that. Depending of course on the size of your shaft.
And than there is the rotation of Earth around the sun. Now, you might add that this is not a problem, because you would be in free fall and earth is too. But that would only not matter if the earths rotation axis would be at 90° to its orbit. So, If it is summer or winter (not spring or autumn), and you are at the summer side of the earth half, you rotate faster around the sun than earth and whenever you are at the winter side, you rotate slower than earth around the sun. Im not sure how large this effect is, pretty small I guess, but since you have presumably only a few meters of shaft, a slight change in orbit will smash you into the wall.
Have fun!
Semmel
I always use to wonder if there were a cavity created at the very center of the earth will you be able to float in the middle sine you were being pulled equally by the earth from all around you.
"We have a precession period of roughly 26000 years. In that time the rotation axis draws a circle at the north pole with a radius of about 1000km. In 45 minutes, this translates to a movement of 1.3m."
am not sure how you calculated... but something seems to be off. If the radius is 1000km then total distance is 2rPi.. or roughly 6000km (Pi=3 for easier math). Now 6000/26000 is roughly 0.2.. or 200meters per year. Then it just can't be 1.3m every 45 min... maybe half a meter every day.
Also the gravity of Sun and Moon will hardly matter much if you're traveling 40.000 km/h and your trip is 20 min.
If acceleration continues all the way to the centre of the earth then so does the increase in pressure. In the air filled case your speeds must be widely optimistic. Surely with a dry adiabatic lapse late of about 10C/km, it will get pretty hot if your tunnel walls are perfectly insulating, or generate some horrendous convection currents if not. Either way, the air must surely be compressed into a liquid, with a corresponding dramatic reduction in terminal velocity, before you have barely started .
Cool idea for an article. Good material for a high school physics teacher I suspect. But if there's an elevation issue on the south pole, why not just start at the south so you can go flying out at the north? Or am I missing something? There are always jet packs with booster and attitude correction too. Who cares about the stinking moon.
@VDGG
if everything was ideal (vacuum, no outside influence except gravity).. you would oscillate until eventually you reach an equilibrium somewhere in the center of mass. But I don't know after how many years.. probably many many.
@Sinisa and VDGG
I think you are wrong. I'm pretty sure that inside a hollow sphere net gravitational attraction is to the inside surface. i.e. an object released in the hole will "fall" until it lands on the inside surface.
SL, you'd keep going, the only thing that would slow you down is friction losses. But only gravity doesn't do that. Well, you may lose attojoules through gravitational waves being emitted by your oscillations, but I think we can discount that.
David, inside a spherical mass, the gravitational mass felt by an object within that spherical body is equal to the mass of the body that remains closer to the gravitational centre of that body than the object in question.
Inside a hollow sphere, you see no force. But you're still moving and will continue at the rate at which you fell out of the shell into the centre until you arrived at the other side. Possibly, if no hole existed, at some speed.
"the gravitational centre of the earth-moon system changes over time"
As SL says, over the travel time considered, they are effectively immobile.
"Than there is the precession of the earth due to the inclination of the moon and earth"
Ditto.
"And than there is the rotation of Earth around the sun"
Ditto.
@David L:
If you do the math you'll find a net gravitational attraction of zero anywhere inside a spherical shell. At the exact centre, you're attracted equally to all points on the inner surface of the shell. As you move along a radius, you get closer to a portion of the shell, *but* the increasing mass of shell behind you actually balances the attractive force exactly.
I remember doing this calculation back in university for Coulomb's law with a spherical shell of charge. It should be the same for gravity (or any r-squared law), no?
@Semmel: When I crunch the numbers (following Sinisa's approximate example) on my calculator, I get a total motion of about 20 mm in 45 minutes due to precession of the Earth's rotation axis. I'm not sure how you get 1.3 m out of that calculation.
When considering the gravity of the Sun and Moon, remember that when you start the journey, you are sharing the motion of the Earth (it's a solid body). That gravity is going to accelerate you, too, in the same direction (if not with the same magnitude) as the Earth is accelerated. The arc subtended by the Earth around the Sun in 45 minutes is about 0.5 milliradians. The worst case scenario would be if you're starting from the subsolar point and the effect is first order in both this angle and the ratio of the Earth radius to the orbital radius (I suspect, but haven't done the calculation, that it's actually second order in at least one of these variables), you get something of the order of a kilometer of displacement at the center of the Earth, and negligible (because the effect during the other half of the trip is opposite) at the endpoint of the journey. The Moon effect may well be worth worrying about, because it involves a smaller orbital radius (order 10,000 km; I didn't look up the exact number) and a larger arc angle (about 6 milliradians).
"I remember doing this calculation back in university for Coulomb’s law with a spherical shell of charge. It should be the same for gravity (or any r-squared law), no?"
It's precisely the same.
Though the proof of that (and its exactness) depends on the object in question being a point source or at the very least spherical and spherically symmetrical itself.
You're most likely to see bigger discrepancies in the path taken in this tube based on the variations in density in the magma and inner core.
Why would the terminal velocity increase as you go down the air-filled tunnel? Terminal velocity is the velocity where the drag force is balanced by the force of gravity. Air density is going to increase the further down you go, while the force of gravity is going down the closer you get to the center (because due to the hollow-shell effect explained above, only the amount of mass that is closer to the center than you are pulls you down), terminal velocity should be going down.
@Wow
a bit of clarification if you can. you said: "SL, you’d keep going, the only thing that would slow you down is friction losses."
If you have a body like earth (not hollow sphere) and you dug a tunnel like in ethan's example, and we disregard everything else except gravity. Then if you start let's say at north pole, you accelerate to center, and then you decelerate as you move towards south, because the center of gravity is acting in opposite force to your direction. Eventually you slow down, stop and start falling back in towards the center... you pass it, decelerare... and back again... Just like an oscilator. No?
But Einstein showed that there will be "gravitational" friction between such an object and our big sphere with a tunnel in the middle. Thus, some small, miniscule amount of energy will be lost by every oscilation. So thus.. in time.. it will have to either stop.. or be in state of lowest energy configuration of a system.. in this case I think a stop.. or some small oscilation around the very center.
Why do you say that it will keep on going.. it can't act like perpetum mobile. Which part did I miss?
Thanx
You mean like when I said this:
"Well, you may lose attojoules through gravitational waves being emitted by your oscillations, but I think we can discount that."
?
I mean you may as well point out that since you'd be screaming out and facing "down", your breath will slow you down.
"Why do you say that it will keep on going.. it can’t act like perpetum mobile."
If your oscillation will last longer than the half-life of the protons that constitute your mass, then in what sense do you ever come to a stop?
Well, it seems I got something wrong. My text was written in a hurry and I didn't double check, my bad. I calculated in this way: The angle would be a = 360/26000/365/24/60*45 using small angle approximation, this translates to 1100*a=1.3 (I guess the radius is closer to 1100km than 1000km). I assume thats wrong and needlessly complicated and wrong.
You are right, the effect is far smaller. Still I'm not convinced that you can rule out the influence of the moon. It sets the centre of gravity outside your tube and for the fall to be successful it is important that the tube goes through the centre of gravity. The centre of gravity of the earth-moon system is roughly 4500km away from the centre of earth. So you will be kind of orbiting the common centre of gravity when you start your fall. But you are falling inside the earth, so by the time you reach the centre, the gravitational effect of earth on you will be 0. So wouldn't the moon pull you in the wall over time? The effect does not need to be large because your tube is so small compared to the size of earth and moon and their motions.
"The effect does not need to be large because your tube is so small compared to the size of earth and moon and their motions."
Who said the hole had to be 3ft across?
@Wow
"If your oscillation will last longer than the half-life of the protons that constitute your mass, then in what sense do you ever come to a stop?"
didn't know it was THAT long :) My instinct was that it must be a long long time. I don't know how one calculates that. But didn't imagine it would be more than proton's HL. Nice. Thanx for info.
I would not start at the South Pole. Reaching a height in the neighborhood of 9000 feet on the North Pole end sounds fun, until a gust of wind makes you miss your return entry into the hole.
By then the North Pole will be ice free.
Still, a drop into shallow water from 9000 feet will kill you, so you'd best not anyway.
Semmel @22: Your method for computing the axis shift due to precession is correct, but you should be measuring angles in radians, not degrees. That makes the result smaller by a factor of 180/π or about 60.
I agree that motion around the Earth-Moon barycenter is something we might have to worry about.
You can calculate *approximately* how much energy you'd radiate if your tensorial maths are up to the job.
The closer to equal size the two objects are, the bigger the effect, biggest if they are equal, then the total mass does as much moving as possible around the common CoM. Faster they go, the more energy in the wave (standard classical wave mechanics), so they need to be close to each other for best effect. And the more massive they are, the more mass is doing moving, therefore the greater the energy loss.
Apart from going a few km past the CoM, everything is against this situation.
I probably overstated attojules (per pass), but it's probably attowatts to picowatts or thereabouts.
Nice discussion Ethan and Folks. Thanks.
Sinisa Lazarek
I had never heard of "gravitational friction". Internet search shows it to be an interesting idea. Thanks for that idea.
I have a question about this "gravitational friction" idea.
Here is a quote:
"X-rays from a black hole are emitted from its accompanying accretion disk -- a pancake-like disk that is formed of the matter dragged toward the black hole (by its gravity) that accumulates over time. The disk reaches extremely high temperatures as the mass of matter from stars and gas swallowed by the black hole cause FRICTION, and it's this that causes it to emit X-rays. These X-rays are used by astronomers to hunt for the black holes, which are otherwise invisible to us." from Black hole's spin measured accurately for first time is near speed of light. Feb 28, 2013 http://www.wired.co.uk/news/archive/2013-02/28/black-hole-spin-explained
My question, is the above FRICTION (my capitals) an example of gravitational friction? Thanks for any clarification.
I also see that "gravitational friction" is mentioned as responsible for slow roll inflation arXiv:1112.1083
Any clarification as to what this means (in words I can understand) will be appreciated.
I would be kind-of curious what the atmospheric pressure at the center would work out to be in the 'air filled' version. Given that the gravitational attraction decreases as you descend, I'm guessing it would be lower than a 4000 mile column of oxy/nitrogen mix would suggest, but I'm also pretty suspicious that it would still quickly reach pressures that would kill an unprotected human being...
Kyle@30 - The world record for (non-enclosed) scuba diving is ~330 m (in seawater). If we take that as a limit, and the fact that air at sealevel is about 800-900 times less dense than seawater at sealevel, one would reach the non-enclosed pressure limit for a human being at about 280 km into the tunnel, neglecting gravitational gradient effects. That's safely into the mantle, but still not very far along.
@Kyle
"I would be kind-of curious what the atmospheric pressure at the center would work out to be in the ‘air filled’ version."
I suck at math, but at one point the air would liquify and thus won't be compressible no more and the pressure would then be like in liquid, but don't know the density. My guess is in range of hundreds of thousands, if not millions of bars.
@RM
it's not the depth that's limiting it's going up and various toxic effects that gases (including oxygen) have with raised partial pressures. You could in theory dive to 1km on scuba, provided you had hundreds of stage tanks, that you were crazy, and that you would decompress for ages and even then probably get bends.. but you could survive. So there are no limits as such... But of course we are not built to exist in 100 bar enviroment...
In any case, no one is arguing that a human can survive in the middle... just a question of what the pressure would be regardless of us.
the more I think about liquid air, the more amazing that hypothetical center of earth would be. I mean huge preassure, but also huge temperature just from that pressure. So liquid air but actually molten lava of air. Would it behave like a superfluid? hmm..
"My question, is the above FRICTION (my capitals) an example of gravitational friction?"
No, that's standard ordinary friction a' la "things keep hitting each other and sharing energy out between each other".
"I suck at math, but at one point the air would liquify and thus won’t be compressible no more and the pressure would then be like in liquid"
Not necessarily, depending on the dynamics of the actual state.
E.g. think of this: pressure increases temperature, increased temperature means melting.
NOTE: pressure has no source of energy to maintain temperatures, and the atmosphere of the earth is warmed almost entirely by the earth's surface being warmed from the sun. NOT by its pressure.
This would NOT be the case if the earth had no surface, as with this hole in the earth.
We've already removed warming from the molten core.
"Would it behave like a superfluid?"
No. A superfluid is from quantum exclusion and a low enough temperature for that to make a difference to the whole.
It's cold not heat and density that make helium superfluid.
http://en.allexperts.com/q/Physics-1358/Pressure-Liquid-Nitrogen.htm
The short answer is "it depends". Without venting, there will be an equilibrium point, but the phase diagram for LN2 shows the critical point as being at 126 K (-233 degF) and 3.4 MPa, or roughly 33.5 atmospheres (493 psi). Beyond this point, the nitrogen becomes a supercritical fluid, e.g., there is no distinction between liquid and vapor, but only one phase.
You state that the speed of free fall at the very centre of the Earth (in an evacuated tunnel) is 11 km/s. I was struck by how close this was to the escape velocity from Earth's surface, and indeed if one uses the gravitational potential energy formula GMm/r, where M is the r-dependent spherically enclosed mass, and used that to calculated kinetic energy at the Earth's center, one does find that the speed is identically equal to escape velocity.
However, a direct calculation of the work done on the person as he falls, as well as other sources, eg hyper physics and even some of the other comments,, state that the maximum speed would actually be equal to near Earth orbital speed, and not Earth surface escape speed.
So wouldn't the top speed be around 8 km/s?
(Sorry if this comes off too blunt... I've never actually written a comment like this before, and the fact that I'm typing on an iPhone right now does n
... not help.
Stupid iPhone.
I think it's just one of those co-incidences, JK.
@ Wow
"and the atmosphere of the earth is warmed almost entirely by the earth’s surface being warmed from the sun. NOT by its pressure."
yes, but we are talking about the middle of earth here. Not the surface. At the surface we have 1 bar of pressure. There's 6300 km to center. One would have to calculate air pressure at that depth. So thus with rise of pressure there will be rise of temperature. Not talking about the magma.. just temperature from pressure. But in case of air, it will depend on the radius of a shaft as well and total volume. Calculating pressure for gases is much more complicated than fluids since they are compressable and is beyond my skill :)
If the gas turns to liquid in the hole, will there be any atmosphere left for us who aren't crazy enough to jump in? Or how much of the atmosphere would fit in a 1m/3ft wide hole through the core
"yes, but we are talking about the middle of earth here."
We're also talking about a cryogenically cooled hole through the earth here:
So, despite the pressure and temperature gradients all the way down, despite having a liquid, molten outer core and a radioactive nickel-iron-cobalt inner core at over 4000 °F, let’s assume you’ve created something that will stabilize your cylindrical shaft, creating a true bottomless pit.
Josef, not all of our atmosphere, though it would be complicated by the compression of the air, the answer would be calculated:
10km * 6000km^2 * pi = V
0.25m * 12000km * pi = v
and the ratio v/V is how much would be sucked in with no compression. With maximum compression (i.e. all in that hole is liquid/solid), it would be 1000v/V.
@Wow
"We’re also talking about a cryogenically cooled hole..."
no no.. forget magma, forget nickel core.. forget how would one even built it.. doesn't matter.
Just a sphere with the mass of earth. And a shaft let's say 2 meters wide and 6 300 000 meters deep. What is the air pressure at the bottom (disregarding all other influence except gravity)? I don't know hot to calculate that, but maybe someone does and has a time to do it :)
Mass of the air above it, at least initially, 1 atmosphere.
As the airmasses reach equilibrium, central pressure will increase to the mass of air that can be sustained above will not be 600atm, though, but somewhat lower because the gravitational force of the air in the column is reduced as it drops.
I may be starting off at the wrong point here, 'cos I'm not checking my physics here, just typing off the top of my head.
You'd start off with integrating the number of moles of atmosphere you would get at 1atm in the tube for each point along the tube, multiplied by the gravitational force at that point, multiplied by the mass of 1 mole.
That would then give you the pressure at each point.
The short version is that at the centre, it could be that it is still 1 atm (if you don't allow the atmosphere to be heated above a human-comfortable 15-21C by the surrounding magma/core.
But it wouldn't be more than 600atm.
So if it does liquify, with liquid air weighing in at about 700 times the weight of the air we breathe, it could suck up most of it. I want a fair bit of promises before I allow any of you to start digging
@Wow
something doesn't add up to me. You say "The short version is that at the centre, it could be that it is still 1 atm"
How come? At the surface, the pressure is 1bar. That's the value of some 30-40km vertical column of air pressing on you. At the bottom of our shaft you will have 6300 km column of air pressing on you. So how did you arrive at 1 bar at bottom? I don't think it will be 6000 bars.. because air pressure rises and falls exponentialy, but can't understand 1bar :)
It won't liquify, you'd need 700 atmospheres.
If it did, you'd get a multiple up to 600,000 atmospheres, but would still not suck up ALL the atmosphere.
"How come? At the surface, the pressure is 1bar. That’s the value of some 30-40km vertical column of air pressing on you."
under 1g of acceleration.
But inside the earth, it isn't 1g any more.
Indeed at the exact centre, you have no mass pressing down and therefore need no pressure there to maintain the mass.
Also note that the pressure reduces with height, so that's not 1g/cc mass of air for 30km.
It really does work out to about 10km of atmospheric mass at sea level density.
(not pressure, density)
I think the molten lava - or radioactive nickel core - down there is under a fair bit of pressure although there's no gravity pulling it anywhere but towards the moon. All air above the center will be pushing down. The first 600 km I guess you'd hardly notice the effect of diminishing gravity.
It's being deliberately warmed, Josef.
We're discarding heating from the radioactive elements and the fossil heat from the collapse (and energy released from the phase change of the mantle/outer core around the solid core as it freezes).
"All air above the center will be pushing down. The first 600 km I guess you’d hardly notice the effect of diminishing gravity."
You don't notice any extra pressure when you're 3 miles down a mineshaft.
And already at 38 atm does air turn into a supercritical fluid, but then only at 36 times the density of our air
Only if you cooled it.
See above re Liquid Nitrogen.
"but then only at 36 times the density of our air"
Can you prove that?
Again, the theoreticians are left at a complete impasse as to the implications of their equations and it remains for the experimentalists to bring any resolution here.
As it is not an election year, government money may be a bit easier to shake loose for this, but determining the right target agency could be an issue. On the other hand, peripheral data generated in the analysis of the core samples that will need to be extracted before final excavation can begin may be of use in the private sector, so alternate funding sources could exist. The grantsmanship for this project must already be in the works.
See also my post #7
Wow , solar heating does only occur at the surface, and causes convection, but the effect that this has on the variation of temperature with height is minimal. A column of gas will be unstable unless it cools vertically at its adiabatic lapse rate, about 1.8C/1000ft. Attempting to keep a column of air hundreds of kilometres high at a constant temperature would produce some horrendous convection currents.
Pressure does increase down a mine whether you notice it or not. So does temperature. About 40% of the increase would be present if there were no geothermal gradient.
An unprotected person moving down the bottomless pit would be cooked well before suffering from the increase in partial pressure of oxygen
I you can't be bothered doing the maths, try the link below. It accepts negative altitudes. Bearing in mind its purpose. it almost certainly does not cover the effects of reducing gravity, but it shows you will hit T&P limits well before this is a significant factor anyway.
http://aero.stanford.edu/StdAtm.html
Yes, David, you are correct. However, I've not said otherwise.
And we're talking about a hole into the ground, not a column up in to free air.
I think you need to reread the thread, you have entirely the wrong end of just about every stick here.
And that link (I've seen one very much like it elsewhere) uses the STP at the surface of the earth where it warms the surface.
And you see that statement "the warming of the surface has no effect on the variation of temperature with height"?
Here's where you're thinking entirely wrong. The height of the tropopause at the tropics is 17km, the height of the tropopause at the poles, about 12km. And the temperature of that tropopause is reversed: the polar air is warmer at ITS tropopause than the tropical air is at its tropopause.
Because the surface temperature is lower at the poles than the tropics.
Thermal winds are caused in the upper air where you have air at similar locations in the atmosphere with different temperatures.
The Jet Stream is one example.
And for anyone interested or gulled by the denier meme of "The temperature at the surface depends on pressure, that's why Venus is so hot at the surface, at 90atm pressure!!!", something to note is that Venus' upper air at 1 atm pressure is still hotter than the earth's surface average by quite a lot.
Surface temps are related not from the bottom up, but the TOA (top of atmosphere, where the average radiation level out into space is) down (via the lapse rate).
And no radiation from the opaque surface (e.g. no earth at all, only transparent gases: no radiation out to space. No TOA, no lapse rate (even if gravity were still there), and the STP calculations aren't usable.
That's similar to the problem of pressure at the centre of this tube: no apparent air column , no pressure, but that's just because the easy method of calculating air pressure doesn't really work here.
When I put -6.000.000 meters in to that calculator,
I get not that huge pressure.. only about 16 bars.. But density... omg... 1488996 kg/m3 and a temperature of 39 000 C !!!! :D
Which would radiate strongly in the transparent IR bands cooling the airmass down quickly without extra heat going in from somewhere else.
The sunlight from the sun at the poles isn't going to be enough!
something is definately wrong with the calculation because air at 16bars can't have that density which the program puts.. but still was fun to try
The question of the moons affect can be easily calculated. Suppose you start off in the very center of the well, floating at equilibrium in zero-g. Since we already know the distance, orbital velocity, and mass of the moon, how long would it take the moons gravity to pull you into the side of the wall? (Assume a 25m tunnel radius.)
Dang, so here's our fix. Instead of free fall, the tube now has rails at 4 points. Into these rails we set a rigging and harness which we strap ourselves into. Now we no longer need to account for anything that'll cause us to smash into the side of the tube, but our speed will now be hard to determine because of friction in the railing system.
Alternatively, we can simply increase the size of the hole to account for any deviation the moon might cause, even at it's closest and somehow magically held in one position during a solar eclipse. How big would the hole need to be?
By "size" I mean diameter of course.
I think it would be more fun to design the tube so that it has a constant width but bends as necessary to accommodate any deviation from the straight path.
Of course this would only work at certain times and after a while as the position of the moon changed you'd end up hitting the wall, but that's where the fun comes in.
Oh, did I forget to mention I was planning to throw my enemies in the hole, not jump in myself?
I guess that would have been good to mention.
Then plug the hole...
I think the success of such a fall would depend on who built the tunnel.
i learned alot
I am going to link to this blog post from my Skydive Earth Sandwich Project page
http://canwefly.com/antipodal-skydive/
You guys might like this...
Actually it is almost as fast to go around the Earth. The trick is to make an evacuated tunnel transport system that lets you go around with enough speed so the acceleration gives you a g force against the ceiling of the tunnel.
That way you can have 2 g of acceleration but only feel 1 g because the other 1 g counteracts gravity.
Using the equation for centripetal force:
v^2/r=a
v=sqrt(a*r)
dist=pi*r
t=dist/v = pi*r/sqrt(a*r) = pi*sqrt(r/a)
pi*sqrt((6,371,000)/20) seconds
= 1773 secs
or 29.55 minutes. So you could get to the other side of the world in just under 30 minutes, and back again in an hour.
If you can stand 3 g, not too hard, then you can get there in
pi*sqrt((6,371,000)/40) seconds
1254 seconds
and you can get there in 20 minutes, 54 seconds and beat someone who goes through the center of the Earth.
Your hole is through. I see you can jump in, so are to climb out?
he tried
once you get to the center of the earth you come to a complete stop cause you are getting pulled from all directions thats how great earths gravity has
@no name #82: Not really. It would be useful for you to read the full post again. If you _fall_ to the center of the Earth, by the time you get there you're moving really fast, so you zip past the center, out the other side, and keep going back and forth like a pendulum.
Or do you also believe that pendulums don't actually swing, because gravity always pulls downward, so at the bottom the pendulum will just stop?
no name:
Michael is right. You would fly right past the center of the earth and (assuming no friction) back up to the surface on the opposite side. The thing you appear to be confused with is that there is no net gravitational force acting on you when you are at the center of the earth. That is true, but no net force means no acceleration. By definition, no acceleration means that your velocity does not change. Since your velocity upon arriving at the center of the earth is non-zero, it will continue to be non-zero as you speed past the center. Of course, your velocity will decrease as you move farther from the center of the earth. You will eventually come to a stop at the surface of the earth on the opposite side of the hole (assuming no friction; if there is friction, you would stop before reaching the surface).
What would the force of impact be if you dropped two 160 pound people that were exactly the same shape that met at the exact center and impacted with exact symmetry? Would they just pancake together and stop, or blow right through each other and keep going in a mixed up paste?
I bet some were there some christian digging theis thing and the church is prbbly founding it