"Where you used to be, there is a hole in the world, which I find myself constantly walking around in the daytime, and falling in at night. I miss you like hell." -Edna St. Vincent Millay
It was just a little while ago that we were all speculating wildly -- and optimistically -- about Comet ISON, as it plunged towards the Sun from its origins in the very, very distant Solar System. As its perihelion date (the moment of closest approach to the Sun) drew near, you may have noticed something interesting about photos of the comet: it's tail appeared to get longer and longer!
If you compare this to earlier photos, you might think it had something to do with flying too close to the Sun, à la the Icarus and Daedalus myth. But it has a lot more to do with the physics of gravity than with anything melting due to heat!
Don't believe me? Take a look at this video, captured by NASA and ESA's great solar observatories, and pay particular attention to the speed of the comet.
Is this a trick of the angle from which we view the comet?
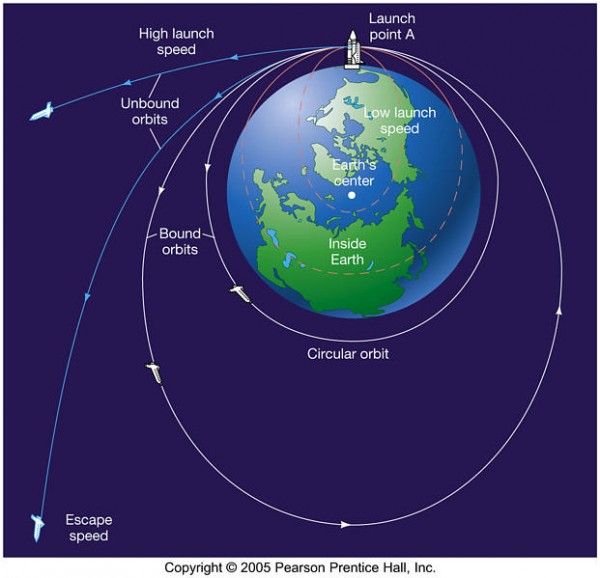
Not a chance; that's just gravity. You see, you might be familiar with escape velocity, or the speed at which you'd need to travel at in order to escape the gravitational pull of a massive, centrally located object.
From the surface of the Earth, that's something like 25,000 miles-per-hour (40,000 km/hour).
But a lesser-known application of the same physical laws and properties tells us that if you dropped an object from almost zero velocity in the vicinity of that same gravitationally massive source, it will fall towards that center-of-mass, reaching that exact escape velocity if it collides with the surface of the massive object dominating the system.
For something falling into the Sun from rest an arbitrary distance away, it would be moving at a whopping 617 km/s, or about 0.2% the speed of light, when it hits the Sun's surface. Comet ISON didn't quite get there, but it did get all the way up to 377 km/s, or about 12 times as fast as the Earth orbits the Sun. In general, the closer an object operating only under the influence of gravity gets to the center-of-mass, the faster it moves; Kepler's famous second law is a special case of this.
But the Sun is hardly the most massive thing we know of, and speeds well in excess of this occur naturally, for huge astrophysical systems, all the time.
Consider a typical, Milky-Way sized galaxy; for our Solar System to escape from it, we'd need to achieve a speed of about 550 km/s, and we're already some 25,000 light-years from the galactic center! That means if we dropped an object -- say a much smaller galaxy -- from an arbitrary distance away, it would be moving at about 550 km/s when it collided with us.
More spectacularly, however, two massive galaxies attract each other in the depths of space, creating a trainwreck with cosmic motions on the order of double that -- or at around 1,000 km/s -- when they finally collide!
 Image credit: NASA, ESA, the Hubble Heritage (STScI/AURA)-ESA/Hubble Collaboration, and A. Evans (University of Virginia, Charlottesville/NRAO/Stony Brook University). (Click for an insane version, if you dare!)
Image credit: NASA, ESA, the Hubble Heritage (STScI/AURA)-ESA/Hubble Collaboration, and A. Evans (University of Virginia, Charlottesville/NRAO/Stony Brook University). (Click for an insane version, if you dare!)
This is, in fact, the future fate of our own galaxy; our somewhat bigger sister, Andromeda, is moving towards us at around 40 km/s, from a gigantic distance of a little more than 2 million light years away. By time we meet in a few billion years, the two galaxies will move at a maximum speed approaching that figure -- 1,000 km/s -- relative to one another!
Much more interesting is when we have large collections of galaxies smashing into one another all at the same time! Two spectacular examples are Seyfert's Sextet,
and Stephan's Quintet,
both of which will have their constituent galaxies travel in speeds exceeding that value, relative to one another!
But why settle for groups of five-or-six galaxies, when we have clusters containing thousands?
 Image credit: © Fabian Neyer / Antares Observatory, via http://www.starpointing.com/ccd/virgodeeplarge1.html.
Image credit: © Fabian Neyer / Antares Observatory, via http://www.starpointing.com/ccd/virgodeeplarge1.html.
The Virgo Cluster, shown here, has galaxies whizzing about at around a full 1% the speed of light relative to one another, and many of these galaxies are huge, giant ellipticals some ten times (or more!) the mass of our Milky Way!
You think that's big?
Now, imagine two of these giant clusters falling into and colliding with each other!
 Image credit: X-ray: NASA/CXC/CfA/ M.Markevitch et al.;
Image credit: X-ray: NASA/CXC/CfA/ M.Markevitch et al.;Lensing Map: NASA/STScI; ESO WFI; Magellan/U.Arizona/ D.Clowe et al.
Optical: NASA/STScI; Magellan/U.Arizona/D.Clowe et al.
That's what we've got for the Bullet Cluster (above), cluster Abell 520 (below),
 Image credit: NASA, ESA, CFHT, CXO, M.J. Jee (University of California, Davis), and A. Mahdavi (San Francisco State University).
Image credit: NASA, ESA, CFHT, CXO, M.J. Jee (University of California, Davis), and A. Mahdavi (San Francisco State University).
and cluster MACSJ0025 (at bottom), among many others. These composite images show the individual galaxies in the optical, dark matter (a proxy for total mass) in blue, and shocked, hot X-ray gas in pink (or green, for Abell 520).
 Image credit: NASA, ESA, CXC, M. Bradac (University of California, Santa Barbara), and S. Allen (Stanford University).
Image credit: NASA, ESA, CXC, M. Bradac (University of California, Santa Barbara), and S. Allen (Stanford University).
With maximum relative speeds reaching 4,000 km/s, or around 1.4% the speed of light, these are the largest-scale, fastest-moving giant objects in the Universe, and as our telescopic reach extends farther and farther back, we're only finding progressively more impressive ones! Dark matter plays a huge role here, increasing the hefty masses of these objects by a factor of five or so over what they'd weigh if they were made of normal matter alone, and the highest speeds we see are raised by a factor of about 140% as a result!
So that's a little glimpse at the greatest cosmic trainwrecks in the Universe, at speeds you might never have imagined for something so large!
- Log in to post comments





If Dark Matter was actually made of weakly interacting matter, wouldn't a galaxy that had gone through a collision be devoid of Dark Matter?
The DM associated with the colliding galaxies would have escape velocity when the galaxies collided and would escape the galaxies. That we haven't found any galaxies that don't have any DM, or even any galaxies where the ratio of DM to regular matter deviates from the norm.
Doesn't this rule out WIMPs and similar particles as DM possibilities?
@Denier #1: I think you're missing something in the kinematics. When two galaxies (or clusters) collide, it is the galaxies _along_with_ their DM haloes which collide. The galaxies generally stay gravitationally bound within their much larger haloes. The gas and dust of the two galaxies interact and get tidally disrupted by the encounter (see that great collage at the top of the article). The DM haloes get much less disrupted. If the two systems merge, forming a single bound system, then the two haloes also "merge", overlapping to form a single large halo.
On a separate note, we _do_ have many observations of galaxies with wildly different DM ratios. These are mostly dwarf and satellite galaxies, and they run the gamut from being nearly all dark matter (as much as 90% or more!) to being almost entirely baryonic.
@Michael Kelsey #2: I agree that there has to be something I'm missing if collisions don't result in ejecting all DM. With the way Ethan described it, it sounded like everything has escape velocity when the galaxies collide, but the regular matter loses escape velocity via the interactions you describe. If DM doesn't interact then it wouldn't ever lose escape velocity. The disparity in interaction would cause regular matter to have a sub-escape velocity while DM had escape velocity and the two would be permanently separated.
It is good to read that observations do report varying ratios. I had always thought all elliptical galaxies had to have the exact same ratio to correctly model their spin. I did not know this was not the case.
I understand escape velocity from our sun is greater than escape velocity from the Milky Way *from our position*, since we're far from the centre (and so if we can escape the sun, escaping the Milky Way is a piece of cake). I was going to ask what the escape velocity would be from the centre of our galaxy, but I guess that's very ill-defined: at the very edge of the black hole at the centre, escape velocity is essentially light speed, right? So escape velocity can be anything up to light speed depending on how far you begin your journey from the event horizon of the black hole. Given that fact, is there some privileged escape velocity we could figure out for a given galaxy, or are escape velocities inescapably (sorry) dependent on position?
One other thing: how does 5 times the mass (in a DM-heavy galaxy) end up giving 140% of the velocity? I would have thought 5 times the mass in each gives a gravitational attraction between two galaxies that is 25 times bigger, and an acceleration that is 5 times bigger. Obviously you can't translate acceleration to velocity without knowing initial velocity and elapsed time--so is the 140% you quoted just an accident of how far apart they started and how fast they were moving before they got caught in each others' grip? It seems like that figure could have been much higher.
DM interacts gravitationally, denier.
UncleMonty @5,
Quick answer: 5 times the mass extra results in a velocity that's is sqrt(5+1) as great, which is ~240% as great, or 140% greater. Hope that helps!
@Wow #6 (following Denier #3): I think that was the point of Denier's question. He framed it in terms of individual galaxies, but our best observational data comes from clusters, and Denier's question is quite valid based on that data.
Consider the "Bullet Cluster", which is a post-collision in progress between two middle-sized galaxy clusters. Observationally, we see three very different things, simultaneously:
1) The two groups of visible galaxies mostly passed "through" each other with some tidal distortion, but not disruption, of individual galaxies. That's a consequence of the individual galaxies being relatively small, with relatively large spaces between them.
2) The mostly non-visible ionized gas is highly visible in X-rays, in the form of a wide and deep hot shock wave in the middle region between where the two clusters passed. That's a consequence of the intergalactic medium (IGM) being continuous through each cluster, and interacting relatively strongly via pressure and density.
3) The majority of the mass, observed via distributions of strong and weak lensing of distant background galaxies, is found on the far sides of the X-ray shock described in (2). These two big mass "blobs" (read "haloes") more or less still encompass the visible groups of galaxies (which, as you recall from (1), mostly just passed through one another).
So what's happened in the Bullet Cluster is that the DM (3) really did just pass through, and the visible "small" (by comparison) galaxies went along for the ride. The more uniformly distributed baryonic stuff (the IGM) in the two clusters, crashed and burned, and got left behind :-)
The Bullet Cluster is just our first example of this; other cluster collisions have been found, and follow more or less the same pattern.
Now, with all of that description, Denier's question about what would happen in a galaxy-galaxy collision is quite valid! Naively, you'd expect the DM haloes to do what they did in the Bullet Cluster, and zip through each other, leaving behind an extra-large elliptical galaxy (the result of the merger), without much of a DM halo.
But that isn't what we expect, because the conditions aren't actually identical. The collision speeds will be lower, and the galactic DM haloes are themselves embedded in a larger cluster halo, so they are more likely to capture each other gravitationally, and (over ~ a billionish years) virialize into one big halo with the merged elliptical embedded in it.
Denier: We are seeing exactly the kind of separation you'd expect from weakly interacting matter in several of the cases above.
In broad strokes there are 3 kinds of matter to think about in these galactic collisions: Stars, dust/gas, and Dark Matter.
Stars are extremely dense compared to the other two types, and because of the great distance between them are extremely unlikely to collide with each other -- the Milky Way/Andromeda crash in the future is likely to only produce a few, if any, stellar collisions. Stars do interact with the diffuse gas of the interstellar medium, but that doesn't slow the star significantly because the star is so dense compared to the medium.
The dust/gas of the two galaxies does collide, and so tends to pile up where the collision occurs.
WIMPs or similar types of Dark Matter don't interact with much of anything including itself, so it carries on unimpeded.
So what you'd expect is that in a galactic collision the dust and gas would be stripped off from the galaxy, leaving just the stars and dark matter to continue on. So what you'd expect to see is a large cloud of gas, heated by the collision, with stars and dark matter separate.
And that's what we see! Galaxies with lots of stars, but very little dust, and much more mass than the stars alone can explain. And nearby, where the presumable collision occurred, a large cloud of heated gas
As to the point about escape velocity -- it's important to note that an object will only reach exactly escape velocity falling into a gravity well if it began at infinity. When that is not the case, the object can get going very fast, but only fast enough to reach the same distance it was before gravity slows it down to a stop and it comes back once again.
Well, Michael Kelsey, you beat me to it, and with a better explanation to boot. Very nice. Now where is that 'delete post' button?
When you say "dust," what particle sizes are you talking about? Does this include anything large enough to constitute a hazard to life-bearing planets in the manner of large asteroids?
And, will the increase in ambient gamma radiation be a hazard to life-bearing planets?
By the time Andromeda collides with the Milky Way, humans or our evolutionary descendants will either have become an interstellar species, or will not have done so and thereby gone extinct via the impacts of increase in solar luminosity.
Assume an interstellar civilization spread across many star systems, that has mastered asteroid defense on each of its homeworlds, and has the means to migrate out of any given system before its local star becomes a hazard. Assume that such a civ is spread out across a region of space greater than 5,000 LY, such that some fraction of it will survive an unexpected gamma ray burst anywhere in its range. What other existential threats are likely to be faced by such a civilization between that point and the heat death of the universe?
(Yo Ethan - Consider that a possible question for a column. What purely natural existential threats are faced by an interstellar civ between time X and end-of-universe, and how might they be met? One more condition: no miracles or magic, no Singularity, no "upload" to the Borg or "post-biological life", no travel at faster than 0.2 c, etc.)
@G #11: Quoting from the Wikipedia article, "It is for the most part a type of small dust particles which are a few molecules to 0.1 µm in size." Grain size can be determined quite well spectroscopically.
Observations of the solar system suggest that population scales inversely with grain size according to a power-law relationship (so that large grains are exponentially less common than small ones). [Yes, I need a good citation for this, and I'm having trouble finding one. Sigh...]
Limits on MACHO searches in the galactic halo imply a very low density of astronomically small, but terrestrially large, objects (asteroid/planet or larger).
@Denier#1and#3 ... please reread and rethink Michael Kelsey #2. As so inferred above by Michael and CB, the DM DOES interact ... with itself and with normal matter through the Gravitational Force. Gravity is THE defining measure in these huge interactions. Think WEAK when discussing DM itself or it's interactions with either itself or normal matter. I believe someone mentioned WIMP.
@Michael Kelsey #8 (and all others who have chimed in): I greatly appreciate the time and effort put in to helping me understand. It is just that I don't have a grasp on how something with escape velocity, absent any interaction outside of gravity, becomes gravitationally bound. I had thought that escape velocity by its very definition meant that it has sufficient energy to escape being gravitationally bound.
Changing the size of the aggregate whole, or the speed required so long as escape velocity is always achieved, which Ethan's piece implies is a truth of physics.
I think it was nailed in the first sentence. I'm missing something in the kinematics.
Escape velocity does mean that.
Energy enough to escape isn't in everything. After all, the original cloud, being in the cloud rather than running away, doesn't have escape velocity. It doesn't have infall velocity either, until some energy is lost to friction (absent for DM), but that matter wasn't leaving the cloud either.
@Wow #15: I'm not quite sure I follow your point on how mass in a cloud obeys the laws of physics differently than mass in a clump, but my misunderstanding has greater consequences than just ejection during galactic collisions. With my current thoughts on kinematics, no galaxies would ever have a halo of DM because every particle of DM would always have the necessary escape velocity to prevent being gravitationally bound to anything.
Instead, what you'd have is a diffuse fog of DM that is everywhere with a density that varied inversely with the density of normal matter. In effect, space curved by the gravity of regular mass would act like the curved upper skin on an airplane wing. Particles of DM entering the gravity well of an object would be accelerated by gravitational attraction and lower the pressure density of the DM fog around the object.
It might mathematically look like a halo from inside a galaxy, but there would be no outer edge of the halo. It would just be diffuse DM fog all the way to the next galaxy.
People much smarter than I am have a different understanding, which means something has to be wrong with something I thought I knew. I'll just follow along and see if I can figure out where the error is.
"every particle of DM would always have the necessary escape velocity to prevent being gravitationally bound to anything."
Why?
Where do you get this assertion for every DM particle?
Denier: Ethan's statements about escape velocity were inexact for the purposes you're applying them to. It works fine for estimating about how fast objects will be going in one of these cosmic collisions (probably at least as well as we can directly measure their relative velocities).
An object that starts at rest relative to a source of gravity can only get as far away from that source as it started. If it has an initial velocity, its final velocity will have the same magnitude. That's basic Conservation of Energy assuming no other interactions but gravity, as we can for stars and DM.
But that's also assuming no other sources of gravity, too. Once there are 3 or more bodies, orbits become chaotic, and objects can gain energy relative to the center of mass at the expense of other objects. So one object can get tossed out of the system (meaning it has exceeded escape velocity), while another will move in tighter. And so you get a concentrating effect around the center of mass.
This is how globular clusters become ever-more dense, with densities in the center that are high enough that star collisions do occur, while simultaneously "evaporating" as stars are tossed out.
So it is with Dark Matter, which should actually be more dense closer to the centers of galaxies. Directly proportional to normal matter density, not inversely. With a small constant. You're right that because DM is still very diffuse, the 'fog' does extend far beyond the visible galaxy, out to other galaxies. Like Michael Kelsey said the entire galaxy cluster has a (non-uniform) halo of Dark Matter.
I hope that helps explain why you'd expect Dark Matter to clump even with zero non-gravitational interactions, and why you shouldn't get hung up on escape velocity in that context.
The flip side of the coin is that the reason DM is gravitationally bound to galaxies is because it is believed likely that the galaxies formed in DM over-densities in the first place. So in a sense it's the normal matter that became bound to the DM.
It also assumes you are talking about the matter most distant from the object. But that isn't all the matter, just the bit you took for calculating.
Nowhere does it say all dark matter (nor matter) has escape velocity.
Denier: This doesn’t this rule out WIMPs and similar particles as DM possibilities. Perhaps I can explain it like this:
If you fall towards the Earth you end up approaching it at 11km/s. If you've got two Earths falling towards each other, they each end up approaching at 11km/s, and their closing speed is 22km/s. The two Earths together make a bigger mass. If you were on one but jumped aside at the last moment, your 11km/s isn't enough to escape the bigger mass.
That said, there isn't really anything that "rules in" WIMPs and similar particles as DM possibilities. There's an assumption that dark matter consists of exotic particles, but no actual evidence. I think it's inhomogeneous vacuum energy myself, but sadly this doesn't get much airtime. See arXiv.
@John Duffield #20: It's not obvious to me that inhomogeneous cosmology does anything about replacing drark matter. All it does, as near as I can tell, is do a better job at modelling the spatially varying curvature due to (assumed!) matter distributions.
That means that it's great for getting a better handle on how large scale structure evolves, but doesn't do diddly squat for telling you want that structure contains.
As a particle physicist, and one currently involved in a direct-detection experiment (SuperCDMS), I quite agree with you that there is *NO* observational evidence (yet :-) ) for dark matter being WIMPs, axions, or anything else specific.
The arguments follow two branches, one based on essentially the consistency and completeness of physics (i.e., "everything else is made of quanta, so DM must be"), and the other based on looking under the lamp post (i.e., we know how to build an experiment to detect WIMPs/axions/whatever, so that's what we're going to look for).
If we find a confirmed signal, that will tell us we're on the right track, and can shift from "what is it" to "how does it work". If we find nothing (and the next generation of proposed experiments can get us below the minimum possible cross-section limits), then we know our "completeness" argument is wrong.
Michael, thanks for the quick reply @ 12, and apologies for my slow reply here.
Interesting that the objects follow a power law relationship as to sizes. Even though the human-relevant sizes are rare, we still need to build a viable space defense, starting now, so it's fully operational & well-tested on harmless objects before it encounters a potentially dangerous one.
A power law is inevitable, really.
One thing wallops into another and breaks up into two pieces, both necessarily smaller than the original, and expected value of half the size of the original.
@Wow #23: I have some hesitation about your "explanation" for the power-law distribution of asteroid sizes. You're not wrong, but I think you've oversimplified. A majority of small solar system objects are, we believe, primordial accretions (i.e., planetesimals), not the result of collisions.
I'm pretty sure that, as you say, a power law is almost inevitable if you have repeated collision events (though the 50-50 breakup case is actually quite unlikely, see the distribution of fission fragments from U-235, for example).
I'm not entirely sure you can claim the same mathematical inevitability for accretion. I suspect that the local environment and physics kick in early enough to prevent a multi-order-of-magnitude distribution (which you need in order to observe a power law vs. just linear).
We don't have any good accretion models to span the gap between ~cm size clumps of dust, up to ~km size planetesimals. Such a model could predict a power law, but it could just as easily not.
@ Denier #16 ... So, young man, it would seem to an untrained mind such as mine, that whoever you were discussing 'Escape Velocity' of a group of specific particles, or simply an individual particle with, he or she left you without insuring you had a solid grasp of the relationship between a particle at escape velocity, and the 'object' from which you infer it must be escaping.
It works as such ( or reasonably close for purposes of this conversation): if EV>11.18 km/s to escape a body with the mass of 1 Earth (approx 5.974E24 Kg), then EV must > 617.6 km/s to escape a body with the mass of the Sun (approx 1.989E30 Kg).
So please understand that a particles escape velocity is directly related to the mass of the object from which it is attempting (allegorically) to esape. Therefore, one must have at least a few defined variables to correctly discuss "Escape Velocity" - Mass (in grams) of the body to be escaped, the distance in meters between the two 'Objects' i.e; the Earth and the Particle (say a Proton), and figuring in for the Mass of both the Solar Syatem and the Mass of the Milky Way Galaxy, along with a few other seemingly unimportant values.
Again Sir, a particles "Escape Velocity" is only relevant when certain other 'things" are brought to bear such as the relative Masses and Distances of those objects being discussed.
:)
@Tony #25: I'm pretty sure Denier understood that. The context for his question was specifically the topic of this blog -- the collisions of galaxies and galactic clusters. In that case, the masses involved are much, much larger than Earth's mass, as I am sure that you are keenly aware.
What is more, as I explained in my reply to him, the objects involved in these collisions are generally bound gravitationally into larger assemblages Thus, their collisional speeds are not really either object's own escape velocity, but rather the orbital speed they have in that larger assemblage.
"@Wow #23: I have some hesitation about your “explanation” for the power-law distribution of asteroid sizes. You’re not wrong, but I think you’ve oversimplified."
Indeed a few seconds thought would have ponderment about rates of collision in a power law realm already set up.
Simplification, however, lets you know what the first step is.
It gives the broad picture.
My simple explanation gives a power law of order 2. This is not the power law actually observed. But to get that other order, you need to do some calculation.
However, their method is generally something very similar, just with more effects included and accounted for.
And note: Fission isn't a breakup from collision.
And second note: no, if all states are equally valid results, the average is exactly half way. Down to a few score atoms, the indivisibility of matter doesn't, pun unintended, matter. It is why fission is no counter.
"I’m not entirely sure you can claim the same mathematical inevitability for accretion."
Never tried to do so.
@Wow #27: It sounded to me like you were suggesting that the power-law observed for small solar-system objects was due _entirely_ to collisional breakup (which would be an oversimplification). Sorry for misunderstanding.
You wrote that you didn't like my analogy between collisional fragmentation and fission. You're right that fission is not truly collisional in detail, but it can be modelled relatively well as a billiard-ball collision between a neutron and a large, fragile nucleus (sort of like a BB hitting a glass marble). As you say, "Simplification lets you know what the first step is. It gives you the broad picture."
I think you'll discover that in collisional fragmentation, all sizes are _not_ equally likely. The exact distribution depends on the relative masses of the colliding objects. Since there are more small than large ones, the majority of collisions will be smaller objects impacting larger objects. You can see this most clearly if you consider the size ratio, rather than absolute sizes: since the distribution is a power law, you should see most of the collisions being M -> 2M (or whatever the scale height is).
Suppose the collision is fast enough to cause full melting of both systems (i.e., rather than an impact crater). In that case, you have a net system 3M, and even if we take your "equal split", then you get two fragments of 1.5 M, which isn't half of the original target. In reality, what you'll usually get, just from angular momentum considerations, is a big blob with a small blob thrown off.
Like I said, I _don't_ think you were wrong, nor do I think your comments in #27 were wrong. I'm pointing out a few of the "more effects included and accounted for" which make this a relatively hard problem.
"You’re right that fission is not truly collisional in detail"
It's more that the chances of fission resultants are nowhere near even, Michael. Worse, not all lighter atoms are available in a fission scenario. More problematical are that they will often self-fission again, with the same problems of inhomogeneity.
To simplify to a collisional breakup would be to simplify it quite a long way beyond "simple enough".
@Wow #30: You wrote, "It’s more that the chances of fission resultants are nowhere near even." Yes, exactly so! In fact, the distribution is very clearly double-peaked, with maxima at around the 1/3 and 2/3 masses (for U-23x, around 85 and 170). Which was one of the reasons I brought it up as an analogy. In large body collisions, the same thing applies, though of course the distribution is different: you don't get a flat spread of possible fragment masses, but a peak around small-ish stuff, and another peak around big residues.
The underlying physics behind the two cases are vastly different, and the two distributions have quantitatively different shapes, but the _qualitative_ (i.e. argument from analogy) outcomes are not dissimilar.
@Wow: There's a new preprint out on arXiv (http://arxiv.org/abs/1401.1813) which is relevant to our discussion above on the size distribution of asteroids. Thought you might be interested, so I'm posting here.
In particular, their Figure 2 shows that the true distribution (magenta boxes) is only a (rough) power law above about 1 km diameter. Below that, there is a steep cutoff, with smaller bodies down by three orders of magnitude! I'm fairly suspicious that this is a consequence of observational bias, rather than being a real effect.
The different models they study for generating the distribution (the blue and green points) both track the data above 1 km (probably because they are tuned to do so), but follow the kind of power law you and I were asserting below that. Good to know my (our) physics intuition isn't completely screwed up :-)
I referenced this past article after seeing the recent third episode of "Cosmos". In this episode, there was a similar and even more outstanding simulation of Andromeda and our Milky Way colliding. The photos in this article and the linked ones in Wikipedia of multiple galaxy collisions are eye opening and even more amazing! Thank you Ethan.