Comments of the Week #4: From null results to the Multiverse

"A scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die and a new generation grows up that is familiar with it." -Max Planck

It’s been a great week for learning a little more about our Universe, from fundamental particles to scales beyond our observable Universe. Our new articles at the main Starts With A Bang blog got quite a response over here, and I'm happy to share with you the Comments of the Week, and my responses to them! Let's start with last week's Ask Ethan.

Image credit: Albert Abraham Michelson, 1881.

From Tim Talbert on the topic of Ask Ethan #29: The Most Famous Failed Science Experiment: We need to quit referring to experiments with negative results as ‘failed’. Only when no usable results are obtained (swamped by noise, equipment failure [e.g., a loose cable = superluminal neutrinos], etc.) has an experiment truly failed. Even then, the details of the failure can help the next experimenter make it work.

I've thought long and hard about this one; Tim was the first (but not the only) person to bring this point up, and I have to agree with it. When we talk about failure in a scientific sense, we don't necessarily mean it in a negative light. Even the best and most successful scientific theories fail to hold up to experiment at some point.

Image credit: Heavens Above, via http://heavens-above.com/.

Newtonian gravity's "failure" to predict the orbit of Uranus led to the discovery of Neptune, while its "failure" to predict the orbit of Mercury gave rise to General Relativity. Similarly, the "failure" of the Michelson-Morley experiment to detect the aether gave way to the Lorentz transformation and, eventually, special relativity. Failure is hardly the right word in its colloquial sense, as these represented huge advances in experimental knowledge, and rigorous tests probing the limits of some of our most cherish theories.

The null result of the experiment should in no way color our perception of these tests as a failure; they are simply veils of ignorance being pulled away from the truths of the Universe.

Image credit: BICEP2 Collaboration — P. A. R. Ade et al, 2014 (R).

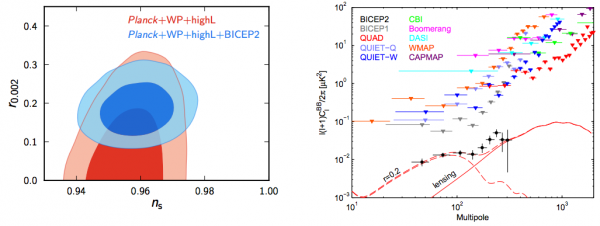
From algernon on last week's Comments of the Week, in reference to inflation and the BICEP2 results: Assuming BICEP2 is confirmed, do you think it’s possible to achieve, during the next years/decades, experimental confirmation of a specific inflation model, among the many available, that actually helps us understand how to properly draw that yellow line, i.e. extrapolating back to times that have left no trace in our Universe? Finding the actual potential of the inflation field, is that doable? Would it suffice?

So as it turns out, there are three things that matter for our observable Universe as respects cosmic inflation: the magnitude (or graphical "height") of the potential, as well as its first and second derivatives, as it undergoes the final 64 e-foldings of inflation. You can visualize this as the final moments of a ball rolling down a hill towards its lowest point, and the shape of the hill -- in principle -- is arbitrary.

Image credit: me, using the Google Graph utility.

There are a number of ways this will show up observationally, including:

• The primordial spectrum of density fluctuations,
• How that spectrum changes with scale/angular size,
• The magnitude of tensor fluctuations (i.e., gravitational waves), and
• How that spectrum changes with angular size.

Measurements of the cosmic microwave background, and its E-mode and B-mode polarization, in multiple different frequency bands (because the signals should be frequency-independent) and on a large variety of angular scales should help us refine which models are viable and which ones aren't. The holy grail could be achieved by a large enough (and sensitive enough) laser interferometer in space that would be sensitive enough to detect these gravitational waves directly. We can't necessarily learn everything about the inflaton field this way, but we can learn and constrain an awful lot. For what it's worth, the best working hypothesis -- if the BICEP2 results hold up -- is that the potential looks like a parabola. (Or, for the bona fide physicists out there, a simple harmonic oscillator.)

Image credit: Jess Laccetti from Edmonton, Canada. Via http://www.jesslaccetti.co.uk/.

From D.C. Sessions on the topic of Should You Get Your Ph.D.: Second the “can’t imagine life without …” part. [...] I’m retired from a fun career in electrical engineering and soon will be going back to school and my first love — physics. Dinner table conversations in this family are sometimes a bit strange, but seriously we can’t imagine doing anything else.

When I wrote this, I talked about what I've come across -- in my (admittedly limited) experience -- as the best reasons for getting a Ph.D. in something. The first one was mine (and many others'), the second was my advisor's (and many others'):

1. Is there something that I need to learn so bad that my life will be incomplete if I don’t go and learn it for myself?
2. Is there something that I enjoy doing so much that I can’t imagine doing anything else as long as I can keep doing this?

There may be other good reasons for getting one, but they don't address "the Zappa question" as I understand it.

Image credit: izquotes.com, retrieved from http://primemag.me/whats-the-point-of-college/.

I've seen so many people stay in jobs they don't like, relationships they don't like, schools they don't like, families they don't like, and so on, because they either feel like it's what they're supposed to do, or because they feel it's too scary and uncertain to go for whatever the thing they really want is. Graduate school in any field is a lot of hard work, a lot of unrewarding hoops to jump through and tasks to perform, a number of classes that are barely relevant to what you're truly interested in and an expensive proposition. Even in science, where they waive your tuition and give you a stipend, you're talking about a huge loss of income compared to what you could be making at a normal job.

So if you don't love it, why would you do it? But conversely, if you do love it -- and you love it so much that you would own one of the two reasons I gave, above -- maybe it is for you!

Image credit: Wikimedia Commons users Frédéric MICHEL and Azcolvin429, annotated by me.

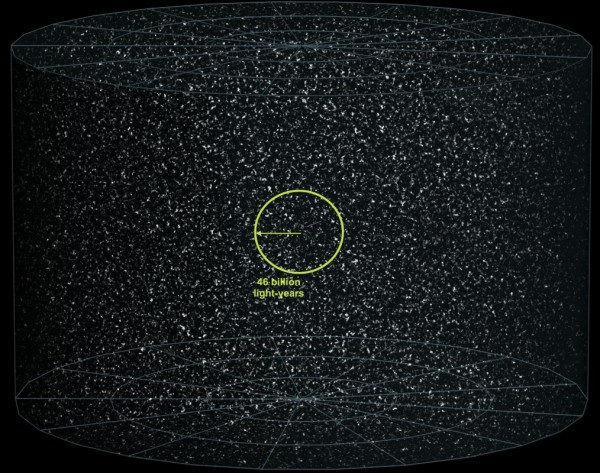
From uncleMonty on the subject of What is the Multiverse, and why do we think it exists?: Ethan, where does the “at least 150″ come from in the ratio of the size of our pocket universe to the size of the observable patch? Is it from flatness measurements? (I mean: is it based on the assumption that our pocket universe is closed on itself, a 3-sphere, that must be huge because the curvature is smaller than we can measure?) Because I thought the jury was still out on whether our universe was finite-but-unbounded–i.e. wrapped around on itself in a higher dimension–or whether it was a simple 3D volume that actually has an edge (just one that lies outside the observable patch). Please, could you clear this up for me?

When we talk about the Universe, we have two things that come together: our theories about the Universe, encompassing the physical laws that govern spacetime and all the particles in it, as well as our observations and experimental results, that point the way towards some ideas and away from others. The way we understand spacetime, we could impose a topological structure atop it whether it's positively curved, negatively curved or flat. But unless that structure is smaller than the size of the observable Universe (and observations say it's not), we have to admit that although it's possible that we live in a finite-but-flat Universe, there's no reason to believe it to be so. So we look at what General Relativity and our observations tell us instead.

Image credit: Rob Knop, via his excellent recent post here: http://www.galacticinteractions.org/?p=1623.

Inflation almost definitely gives us a huge Universe, beyond our (flat) observable Universe is almost definitely more flat, observable Universe, and based on our measurements of curvature and lack-of-correlations of points across the sky, that is where the number of "150 times the size of the observable Universe" as a lower bound comes from. Yes, there is an assumption inherent in that, but it would be a far greater assumption to assume there would be a topologically nontrivial (i.e., toroidal) structure to space.

Image credit: Doug Savage, via http://www.savagechickens.com/2007/01/razor.html.

It's possible, but it's not the simplest explanation.

Hope you enjoyed our latest Comments of the Week, and I'm glad we're all learning so much from each other. Sorry I couldn't get to more, but alas, I haven't figured out how to dilate time for all of you while I write as much as I want! (And a special "thank you" to Michael Kelsey, for dropping lots of excellent physics knowledge in the comments.)