“Sometimes a person has to go a very long distance out of his way to come back a short distance correctly.” -Edward Albee
Every week on Ask Ethan, we've been taking a look at my favorites of the questions you send in. And one of the things you've been wondering about is this: when we look at an object way out there in the Universe, how do we determine how far back in time we're looking.
Image credit: © 2013 Alan Dyer, via http://amazingsky.net/2013/12/10/orion-and-canis-major-rising/.
Is it as simple as measuring the distance to it and calculating the time by using the speed of light? If only. That might work for the nearest stars (and possibly a handful of the nearest galaxies), but that approach begins to break down fast the farther away we look for one simple reason: the Universe is expanding!
Image credit: retrieved from John D. Norton at University of Pittsburgh, modified by me.
So what do we need to do in order to figure it out? Go read the whole thing and you'll know, too!
- Log in to post comments
More like this
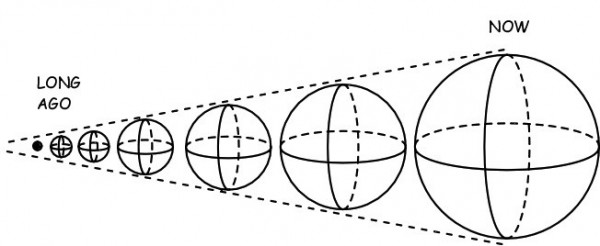
There is a bit of circularity to the logic, we are trying to determine the distance versus age in order to verify the expansion history, yet these things depend on the expansion history. Mathematically, it is an implicit, not an explicit method. So you have to rely upon models, and use the subtle differences in what the models predict we will observe, to discriminate between models, or to constrain the values of adjustable parameters.
@Omega #1: It's almost, but not quite, circular. What breaks the apparent tautology is the use of properties (Cepheid periods, galaxy brightness vs. rotation, Type Ia supernovae light curves) which are strongly correlated to the _absolute_ luminosity of the object in question. If we can determine the absolute luminosity, and then measure the apparent luminosity (i.e., how bright it looks to us in the sky), we can use 1/r^2 to infer the distance.
Spectroscopy then gives us the redshift for the same object (or an object tied to it, like the galaxy in which the supernova went off). So now we have _both_ the distance and the redshift, measured separately, and from that we can reconstruct the expansion history (e.g., Type Ia SNe are visible over a wide range of redshifts, so we can get a whole section of the d-Z curve, not just one point).