“One feels that the past stays the way you left it, whereas the present is in constant movement; it’s unstable all around you.” -Tom Stoppard
You might best know Einstein for E=mc^2, but I would argue that the far greater contribution was the development of relativity. Think about the following: if you strike the upper atmosphere with a cosmic ray, you produce a whole host of particles, including muons. Despite having a mean lifetime of just 2.2 microseconds, and the speed of light being 300,000 km/s, those muons can reach the ground!
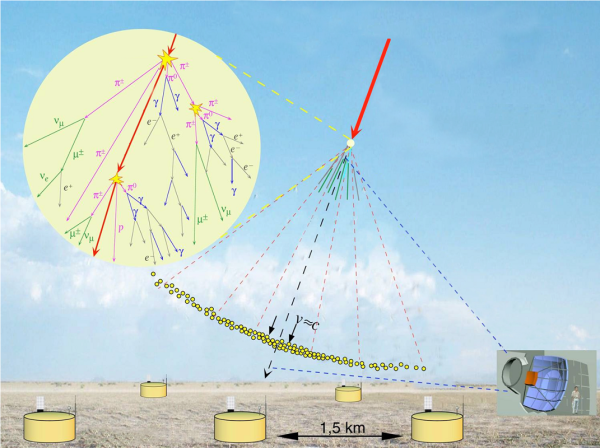Image credit: Pierre Auger Observatory, via http://apcauger.in2p3.fr/Public/Presentation/.
That's a distance of 100 kilometers traveled, despite a non-relativistic estimate of just 660 meters. If we apply that same principle to particle accelerators, we discover an amazing possibility: the ability to create a collider with the cleanliness and precision of electron-positron colliders but the high energies of proton colliders. All we need to do is build a muon collider.
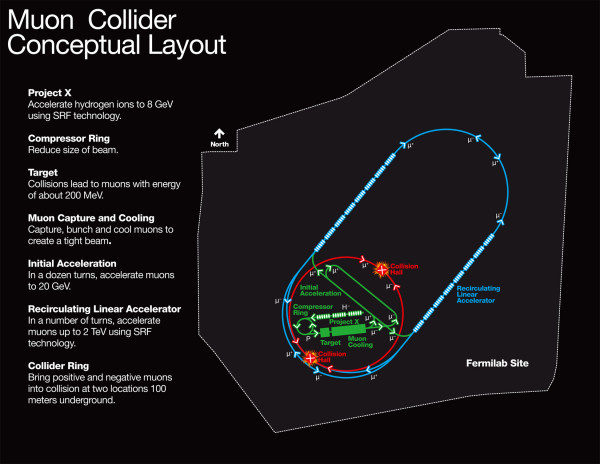Image credit: Fermilab, via http://www.symmetrymagazine.org/breaking/2009/11/19/what-a-muon-collide….
A pipe dream and the stuff of science fiction just 20 years ago, recent advances have this on the brink of becoming reality, with a legitimate possibility that a muon-antimuon collider will be the LHC's successor. Find out more on this week's Ask Ethan!
- Log in to post comments
More like this
thanks for using metric units screw foot/pound
GREAT LUCID ESSAY.. WILL WAKE EFFECT ACCELERATORS BE AN ADVANTAGE TO A MUON COLLIDER AND IS THERE ANY PUSH FOR THIS PROMISING TECHNOLOGY THAT HAS BEEN LANGUISHING FOR MANY YEARS DESPITE ITS GREAT PROMISE ?
As the particles in the beam, as measured in the earth's frame, still decay the beam itself will be radioactive, giving off high energy electrons (or positrons) along its pathway, there will be inevitable leakage of these electrons. How much of an obstacle is this path radiation expected to be?
@Omega Centauri #3: In a muon collider storage ring, the electrons will have the wrong mass (and hence the wrong momentum) to be properly bent by the magnets. Instead, they'll hit the outward sidewalls, which will consequently need to be shielded and extensively cooled, probably with an "alcove" design (a horizontal extension on the outward bend side).
This situation is quite similar to typical electron storage rings (such as the SLAC B-Factory, where I worked on the BaBar detector), which have to deal with the sychrotron radiation from the electrons.
@Thomas Barton #2: There have been discussions about using plasma wake-field accelerator sections for both a muon collider and the ILC. The main issue currently is one of efficiency and dispersion: only a small fraction of the beam gets the full acceleration effect; the rest of the beam ends of straggling in energy from the peak all the way down to the input energy. As you can imagine, that sort of distribution is not useful if you're trying to steer or focus a beam :-(
I'm sure that this has been factored into the design of a hypothetical muon collider, but I had a question. IIRC, in GR, a gravitational field causes time dilation, a phenomenon separate from the time dilation in SR caused by velocity. Since the path that the muons travel would presumably be circular (or at least curved), the muons would be accelerated. GR tells us that acceleration is equivalent (at least locally) to a gravitational field. Would this acceleration cause a time dilation that is greater than that expected solely from the velocity of the muons?
Yes, SeanT, but the maths already includes those effects in it. Most of the effect can be ignored because compared to the time spend whinging round at very high speed before they eventually hit a target the effect of acceleration is not really notable.
And any change in this really doesn't change the effect, just when, precisely, it happens for any one event.
The treatment by the particle physicists will be far more complicated than we'd use (or know) here as non-specialists, and their effects are accounted for in the treatment they would use.
One of the reasons for the whacky notation is to get a "neat" description that doesn't need a plethora of terms added in. Makes it hard to read, though.
Thanks, Wow. I was pretty certain that I hadn't come up with anything that wasn't already accounted for by those with more expertise than I have. I just wanted to make sure that I understood the basics of GR, namely that an acceleration is equivalent to a gravitational field and that a gravitational field/acceleration causes time dilation. I realize that the math is much more complicated than I can reasonably hope to understand, but would you agree that for a layperson, that description is reasonably close? (I am not concerned with whether or not the magnitude of the gravitational time dilation is significant relative to the magnitude of the time dilation resulting from the velocity. I just wanted to confirm that there is a time dilation, at least theoretically, that arises from the centripetal acceleration.)