"Resistance to the organized mass can be effected only by the man who is as well organized in his individuality as the mass itself." -Carl Jung
If you divide the matter we know into progressively smaller and smaller components, you’d find that atomic nuclei, made of protons and neutrons, compose the overwhelming majority of the mass we understand. But if you look inside each nucleon, you find that its constituents -- quarks and gluons -- account for less than 0.2% of their total mass.
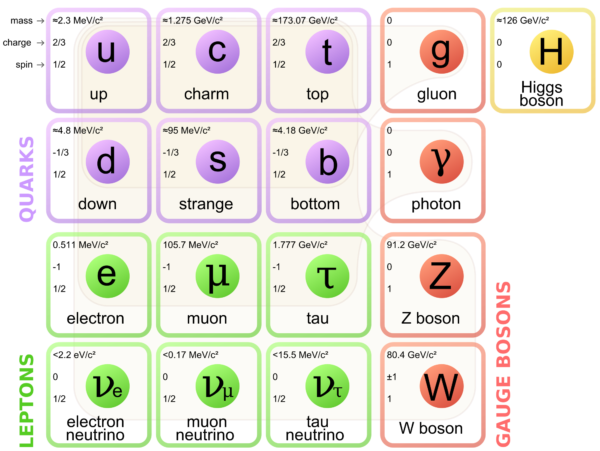 The particles of the standard model, with masses (in MeV) in the upper right. A proton, made up of two up quarks and one down quark, has a mass of ~938 MeV/c^2. Image credit: Wikimedia Commons user MissMJ, PBS NOVA, Fermilab, Office of Science, United States Department of Energy, Particle Data Group, under a c.c.a.-3.0 unported license.
The particles of the standard model, with masses (in MeV) in the upper right. A proton, made up of two up quarks and one down quark, has a mass of ~938 MeV/c^2. Image credit: Wikimedia Commons user MissMJ, PBS NOVA, Fermilab, Office of Science, United States Department of Energy, Particle Data Group, under a c.c.a.-3.0 unported license.
The remaining 99.8% must come from the unique binding energy due to the strong force. To understand how that mass comes about, we need to better understand not only the average distribution of sea quarks and gluons within the proton and heavy ions, but to reveal the fluctuations in the fields and particle locations within.
- Log in to post comments

Whenever someone talks about the need for new particle colliders, as this article does, they often talk about diameter. Occasionally I'll even read an article where it is stated to probe a particular phenomenon it would require a collider the size of our solar system, galaxy, or even universe. Why is this? Why can't you just pump more energy into an existing diameter collider? Would we really need a collider the size of our solar system or could we just build some really big power plants to get the same results from the LHC?
The limitation is the magnets, as worked out here (PDF) in two quick pages.
^ "three quick pages"
@Denier #1 and Narad #2: Kirk's homework problem (he and I, and Chris Tully, all worked together on BaBar back at that time!) actually shows that the limitation is both the magnets and the synchrotron radiation.
The radiation problem is the critical item for electron machines. Why? Because at a given bend radius, the amount of energy lost by the beam scales like 1/m^2. The bend radius is determined by the magnet strength. If you put electrons or protons into the same machine, the electrons would radiate about 3.3 million times as much energy as the protons would.
If you want your beam to go around the machine multiple times, you need to keep the synchrotron losses to a minimum, or have enough input power to keep pumping into the beam. The beam composition, energy and plausible magnet strength, then, are all you need to calculate what size you have to build your collider.
So when I add the masses from the table for 2 Ups and 1 Down I get 9.4 Mev/c^2. If the proton mass is 938 Mev/c^2, wouldn't that be ~1% instead of the ~.2% stated?