"The design of the universe...is very magnificent and shouldn’t be taken for granted." -Charles W. Misner
One of the more puzzling aspects of our Universe is that, no matter which direction we look in, no matter how far away we check, its properties appear to be practically identical. This is surprising, since no signal can reach from one disconnected region to another, and yet the Universe behaves as if everything began from the same initial state. We refer to this as the horizon problem.
 If these three different regions of space never had time to thermalize, share information or transmit signals to one another, then why are they all the same temperature? Image credit: E. Siegel / Beyond The Galaxy.
If these three different regions of space never had time to thermalize, share information or transmit signals to one another, then why are they all the same temperature? Image credit: E. Siegel / Beyond The Galaxy.
Before there was cosmic inflation, today’s leading solution to that problem (among others), there was the idea of a Mixmaster Universe, where a combination of oscillations and growth led to a Universe that got smoothed out by the dynamics of its evolution. Although it didn’t solve the horizon problem in details, the chaotic properties of a Mixmaster Universe provided physical and mathematical insights that are still useful today.
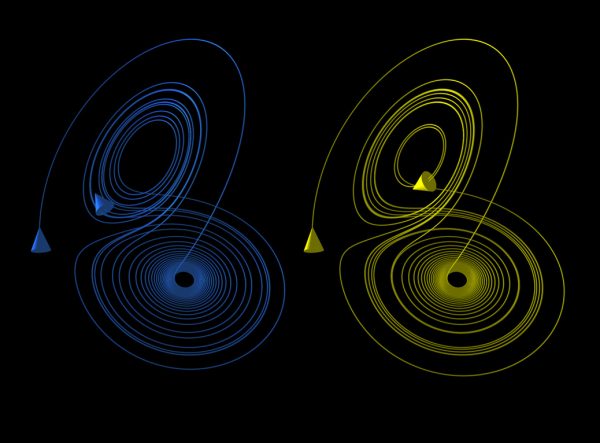 A chaotic system is one where extraordinarily slight changes in initial conditions (blue and yellow) lead to similar behavior for a while, but that behavior then diverges after a relatively short amount of time. Image credit: Hellisp of Wikimedia Commons / Created by XaosBits using Mathematica and POV-Ray.
A chaotic system is one where extraordinarily slight changes in initial conditions (blue and yellow) lead to similar behavior for a while, but that behavior then diverges after a relatively short amount of time. Image credit: Hellisp of Wikimedia Commons / Created by XaosBits using Mathematica and POV-Ray.

first there was nothing ........... then it exploded
“One of the more puzzling aspects of our Universe is that, no matter which direction we look in, no matter how far away we check, its properties appear to be practically identical.”
Tell that to the people on Mars.
Oops! There are none.
And the big clump here and the bigger clumps there,
and here a clump,
there a clump,
everywhere a clump clump,
and then some space for old McDonalds.
Obviously, I must not understand the horizon problem very well.
:)
.
skl,
The issue is scale. On a small scale, sure, the universe appears different from different locations and looking in different directions. If you're looking at scales of millions of light years or more, though, pretty much all parts of the universe do look alike. The density of galaxies looking in one direction is quite similar to that looking in any other direction, for instance.
The real kicker, though is the cosmic microwave background. Right now, if you look out into space, it's transparent. You can see light coming from the moon, planets, the sun, distant stars, galaxies, etc. This was not always the case, however. The universe was so hot at one time that neutral atoms were thermally torn apart into charged particles. These charged particles scattered light, and therefore, the universe was opaque. Once the universe cooled sufficiently for charged particles to combine into neutral atoms, the universe became transparent. We can still see this light, although it's now red-shifted into the microwave portion of the electromagnetic spectrum. This is the CMB.
Now, the CMB is a measure of the temperature of the universe at the location from which it emanates. The universe is just over 14 billion years old. If we look at the CMB in a given direction, we see light that is about 13.9 billion years old. If we look in the direction diametrically opposite, we see light that's also 13.9 billion years old. We see (to within miniscule variations) the temperature of these two locations (and any other locations) to be the same.
How can this be, though? That's the horizon problem. These two locations are separated by too great a distance for them to have had a causal affect on each other. The agreement in temperature is too close to be coincidental. Why should two independent regions of the universe necessarily be the at the same temperature? It's as if Columbus had sailed to the Caribean and found a Native American tribe flying a flag identical in all respects to the Spanish flag he flew on his ships. Sure, it's possible to have happened by coincidence, but it's wildly improbable. Columbus and others surely would have been looking for ways that these native people came into contact with Spaniards without any record of those contacts being made. In like manner, physicists have come up with explanations, with inflation being the currently accepted one, to overcome this horizon problem.
jimbob,
Well, there was never "nothing", and there also was never an explosion. Other than that, you got it pretty well correct.
and all life came from a rock
and life came from a rock
I still don't see the horizon problem.
When CMB photons were created, wasn't universe just a ball of uniform plasma? If its light diffused into whole universe today because of the expansion, why we should expect big variations anywhere?
@jimbob # 5 NO Life came from the Lord most High, God of the Jews and creator of all.
@ SeanT, is there a way to extrapolate the remaining heat in the universe to garner a time frame for the universes birth vs the current temp of outer space?
Thanks
The heavens declare the glory of God
Can't the horizon problem be solved by the notion of these causally separated locations obeying the same laws of physics?
Consider as an analogy a great salty lake in the sun. As it dries, salt crystals form here and there. They are effectively causally disconnected - the formation of a crystal here doesn't impact the formation of a crystal a mile west. And yet, in every place, you always get NaCl in the same face-centered cubic lattice. You don't get NaCl in one place and NaCl2 in another. You don't get a face-centered cubic lattice in one place and a simple cubic lattice or hexagonal lattice in another. You'll get the same structure everywhere, without any need for any causal connection between them, because each place has the same constituents undergoing the same process governed by the same physical laws.
Likewise, I could easily see how two causally separated portions of the universe, undergoing the same sudden formation of neutral atoms, release photons of the same energy. Because the relationship of photon energy to bond formation will be the same, as its governed by the same laws. Just like I would expect that beyond the 'causal horizon' of the Earth, hydrogen gas clouds gravitationally form stars. I don't need to hypothesize some extra reason or mechanism for that to occur - I just have to assume that place beyond our horizon has the same atoms and laws as this place, and everything else follows.
@eric: The horizon problem isn't the common laws of physics, it is (at its most basic) the common temperature of the CMB. Consider various causally disconnected regions in our universe, each with their own quantum fluctuations and energy left over from "the big bang", and let those regions then evolve and expand independently.
Since the expansion rate is the same, you do expect the overall CMB temperature to be about the same across all the regions, but the differences, and the fact that the regions were thermally disconnected from one another, means that there really _should_ be measurably difference (i.e., different at the percent or so level).
But that's not what we observe! The CMB is _identical_ down to the 10^-4 level across the entire observable universe! Regions on opposite sides of the sky, which are _still_ causally (and hence thermally) disconnected from one another, have essentially identical temperatures.
The spatial scale, and magnitude, of the CMB fluctuations (those pretty speckled maps) are at the 10^-6 level and correspond to large-scale structures.
*THAT* is the horizon problem. How did regions on opposite sides of the universe, which have been completely disconnected from one another, manage to achieve perfect thermal equilibrium?
where did matter come from
eric,
That works as far as the analogy will take you, but I know of no physical law that states that photons of the same energy must be released during the formation of neutral matter. The energy of the photon released would be highly dependent on the energy levels of the charged particles that combined. There is no physical law that states that two pairs of causally disconnected ions must have the same energy levels, hence the horizon problem.
You're right, jimbob. We scientists have it all messed up. All our years of study to learn about the universe and get things right, and we missed all those simple objections to our theories. Any simpleton could see that we cannot possibly be right and that it's all just a giant conspiracy theory to promote atheism. You caught us; your few simple sentences just destroyed all of modern science.
Unless, of course, you don't fully understand everything you think you do????
Sean T:
My take on it: a neutral (hydrogen) atom is always going to form at the exact same background "temperature" - 13.6 eV. No matter where you are in the universe, no matter whether it's causally connected to the part you're in or not. Because that's dictated by the physics of proton to electron binding. And because the formation always occurs at the same temperature and is always the same physical reaction, we should indeed expect the photons released to be the same energy no matter where in the universe this formation occurs.
So it's a bit like a type Ia standard candle. Since it always occurs under a specific set of narrow conditions and the resulting system is always the same, we can expect the photon spectrum to always be the same.
Now, my hypothesis above does not explain why this transparency would occur at the exact same moment all across the causally unconnected parts of the universe; parts at different temperatures will have it occur earlier or later. But AFAIK cosmologists don't actually think of recombination as being instantaneous/simultaneous; recombination was a relatively short epoch but still an epoch. So the fact that my hypothesis would predict slightly different times of recombination for different areas of the universe is consistent with it.
I (probably wrongfully?) agree with eric's analogy
Sean T explains:
"The energy of the photon released would be highly dependent on the energy levels of the charged particles that combined."
That may be true, but the release of energy from a cloud consisting of zillions of colliding particles will average to the same number just like the average outcome of rolling a die a zillion times will be almost identical if repeated anywhere in the universe.
So what kind of cause could result in large scale measurable different effect on two sides of the universe just by chance?
@ anneb & eric
Michael Kelsey gave an exact explanation. It's not so much that they are same everywhere (I mean, it is..) but the important part is HOW EXACTLY same they are everywhere.
Eric mentioned salt crystals, and it's a good analogy, but here's the thing... Take two ice crystals from two different parts of that salt lake and really measure their compositions. Sure, chemically they are all NaCl, but each sample will have differing traces of other things. One might have some more water molecules traped.. other might have some dust in, some might have an insect trapped inside etc... While they are all NaCl, each will be "unique". We don't see that within CMB. Another example.. i.e. take a bucket of water and put one drop of paint in it. Take two consecutive samples... the difference in amount of paint molecules in two samples will be more than 10^-6.
That's the issue. In terms of CMB... not only that it's uniform, but how incredibly uniform it is. We don't usually see such uniformity in things on earth and lab.. which are all causally connected and can get into equilibrium, let alone for the whole universe.
So, same laws of physics everywhere is ok, but it doesn't explain the uniformity of such a degree.
IMHO I still cannot see the horizon problem.
My understanding is that the reason for it is this:
Even though CMB started with similar conditions everywhere, after universe expanded for billions of years, even tiniest of differences in different locations would keep adding up and cause CMB to be wildly different in all directions. So it is amazing that CMB is extremely uniform everywhere.
My thinking is that those tiniest differences were always similar everywhere and in the end it is quite normal that CMB is still almost perfectly uniform.
For example, I just created a simple Python program to test it. Each time it adds one million random numbers where each is between 0 and 1, and it prints the result, repeatedly.
The results clear that the final total is always very close to 500000. There is never any big difference.
I used random numbers with uniform distribution in my experiment but I have no doubt the final totals always would be very close the each other. For example I just tested with a triangle shaped distribution (sqrt(rnd)) and the final totals are always very close to 666666 it looks like.
the more science learns about the relation of laws of physics and the universe the more it reveals God THE CREATOR AMEN this much i truly believe
Simple statistics Frank. The averages of your numbers should be close to the distribution mean, so the sums will be close to the same size times the distribution mean. Is that what you were looking for?
@ frank
I'll try to explain through your program.... CMB is not uniform statistically.. it is uniform period.
if you've setup your program to add random numbers between 0 and 1, to 6 decimal places (lets say that simulates differences in temperature during BB) on a surface 1000 by 1000 units. And you end up with number 0.578 appearing everywhere (not average statistical value).. but actually only that number (no 0.215, 0.999, 0.002.. etc). You would certainly think there is a problem with your program. This is a poor analogy, since random number generator doesn't really represent CMB, but hopefully it's close enough analogy in order to understand the horizon problem.
This is why we think inflation happened... it started in that region where i.e. number 0.578 was and stretched it to the whole observable universe, so now only that number is visible everywhere.
Sorry, but that's not analogous. The analogy is about whether Na and Cl atoms will behave the same in causally disconnected parts when under the same conditions...and they do. Exactly the same. So its reasonable to think that photons, free photons, and free electrons will behave exactly the same in causally disconnected parts under the same conditions.
I guess your extension would be relevant if a part of the universe started out with excessive He or Li nuclei. Then okay, yes you'd see a slightly different photon energy spectrum (specifically, additional lines forming at the appropriate temperature and then red shifting into the microwave along with the Hydrogen bonded-produced photons). But variations in the background temperature should not change the binding product photon energy, only the timing in which you get them. Likewise, variations in photon and electron density should also not change the produced photon energy, only the intensity. So it still seems to me perfectly explicable and not at all any sort of horizon problem as to why the CMB is basically the same energy everywhere.
Ah, sorry, there are two instances in that paragraph where I mistyped "photon" instead of "proton." "Free photons" should be "free protons," and "variations in photon and electron..." should also refer to protons.
@ eric
AFAIK the horizon problem is not the problem for the recombination epoch, but for much earlier than that. You are absolutely correct that once the photons were released, they were released under same conditions, then they had the same temperature everywhere.
The horizon problem (due to particle horizons) is more of a uniformity problem before the decoupling. What made the universe so extremely thermally same in the beginning? Is it because the initial conditions were such (fine tuning problem).. or did something make it such (inflation).
For various reasons (which I hope Ethan would cover) cosmologists don't really like option no1. Instead, it's thought that universe wasn't so perfectly homogeneous at the very early stage and it was something else that caused it be so (inflation).
https://www.youtube.com/watch?v=JDmKLXVFJzk&ytbChannel=PBS%20Space%20Ti…