Pi Day Fun Facts!

Posted by Ethan on March 14, 2012
(17)
More »

“Now go on, boy, and pay attention. Because if you do, someday, you may achieve something that we Simpsons have dreamed about for generations: you may outsmart someone!” -Homer Simpson

Today, March 14th, is known tongue-in-cheek as Pi Day here in the United States, as 3.14 (we write the month first) are the first three well-known digits to the famed number, π. As you know, it’s the ratio of a perfect circle’s circumference to its diameter.

Image credit: LeJyBy at Flickr Creative Commons, retrieved from sciencebuzz.org.

It’s also very, very, very hard to calculate exactly, because it’s impossible to represent π as a fraction. (You may remember that’s part of the definition of an irrational number.) But that doesn’t mean we haven’t tried!

The easiest way to try is to either inscribe or circumscribe a regular polygon around a circle of radius 1, and calculate the polygon’s area. The more sides you make, the closer you’ll get.

Image credit: Archimedes' Pi approximation, by Leszek Krupinski.

Archimedes, who discovered the fraction 22/7 (which is why Pi Day is July 22 in Europe), took the equivalent of a 96-sided polygon to do this, and found that π was between 220/70 and 224/71, which is not bad for two thousand years ago!

But it’s hardly the most impressive approximation for π from back then. That honor goes to the Chinese mathematician, Zu Chongzhi.

Image credit: Statue of Zu Chongzi in Tinglin Park in Kunshan, by Gisling.

He discovered — in the 5th Century — the approximation Milü, which is 355/113. Which is equal to, for those of you at home, 3.1415929… meaning you have to go to the eighth digit to see the difference between this number and π. In fact, if we look at the best fractional approximations of π…

Image credit: Gisling.

we wouldn’t find a better one until 52163/16604! (Exclamation point, not factorial!) That was the world’s best approximation for π for something like 900 years, until this guy came along. Pretty impressive!

But what if you wanted to calculate π, but wanted to do as little math as possible? No geometry, just basic counting and four-function mathematics? Well, if you can play darts, you can do it!

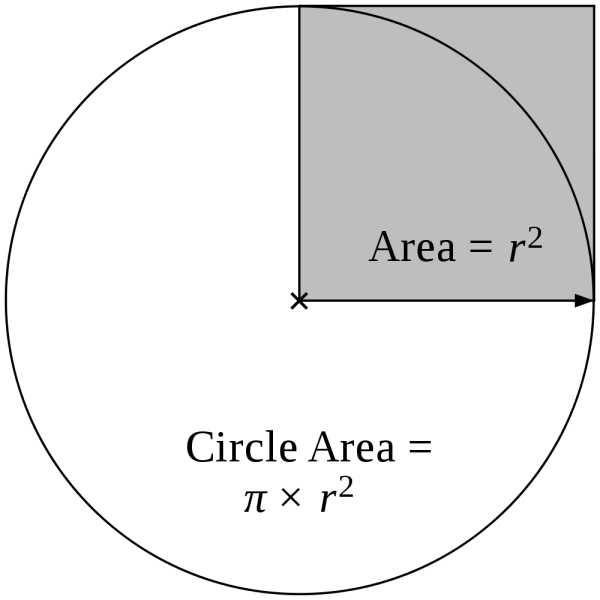
It will only get you to π very slowly, but throwing darts (randomly) at a circle with a square of area equal to the circle’s radius will allow you to calculate π! How so? Count the darts that land in the circle, divide by the number of darts that land in the square, and that’s how you calculate π. (For those of you who write a computer program that can do this, congratulations, you’ve just written your first monte carlo simulation!)

But let’s say you wanted to be more efficient, but you wanted to get to π with arbitrary accuracy, given enough time. Have I got a fun method for you: you can represent it as a continued fraction, and the farther you continue it, the more accurate you’ll get!

i-b74926c08c73034cbf1f7ab80f200390-62971363e3321d4371bd3c8fbed1ae6a.png
For example, here’s the results from the first few terms; not bad!

Pi Day is also a special day for anyone interested in astronomy and space! Four famous astronomy and space heroes have their birthday on Pi Day; can you name them all from their pictures?

(Okay, okay, one of them is easy!)

As far as the pies go, I’m still no good at making pie crust, but I do have a special treat that I can make, with a circumference and a diameter and everything.

Image credit: Jemma.

Yes, it’s a Leche Flan! Hope your day is as sweet as they come, hope that you enjoyed all the fun facts about pi, and if you’re up late over the next couple of nights, enjoy the Pi Day miracle of the Jupiter-Venus conjunction in the night sky!

Image credit: Laurent Lavedar, TWAN, retrieved from National Geographic.

Happy Pi Day!

(And your birthday boys are, from L-R, Albert Einstein, Apollo 8 Commander Frank Borman, Astronomer Giovanni Schiaparelli, and last-man-on-the-Moon Gene Cernan.)

(17)
More »

Comments

  1. #1 HP
    March 14, 2012

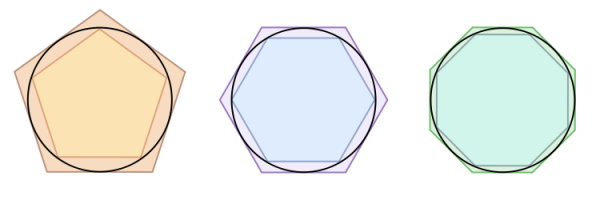
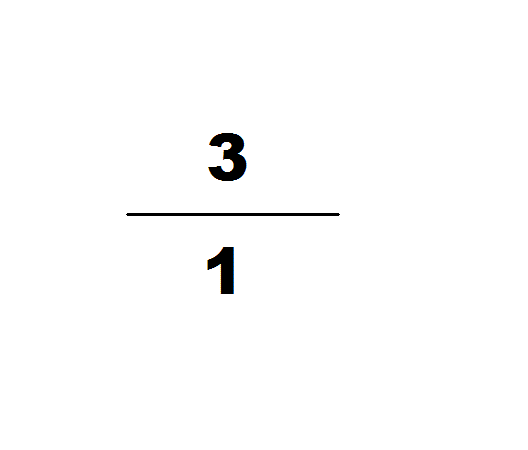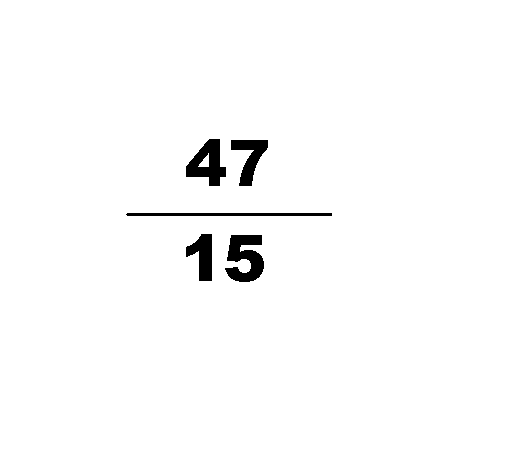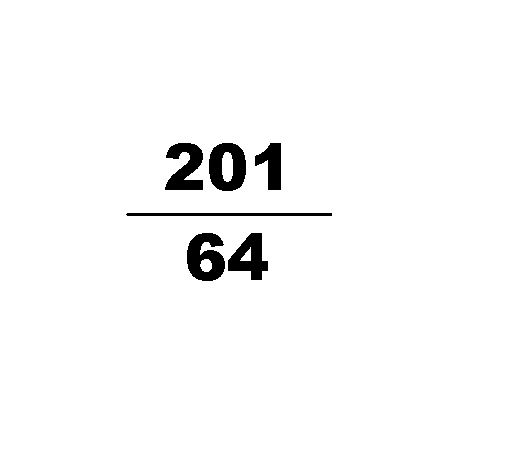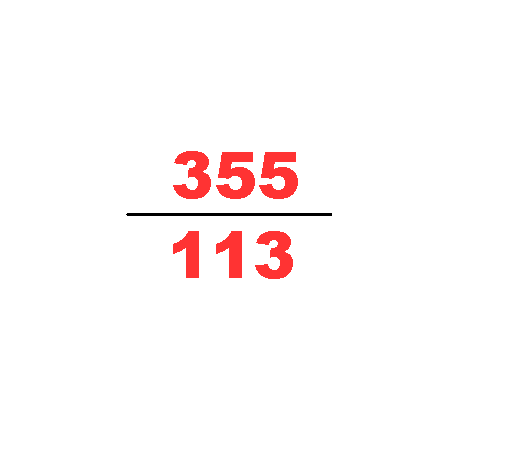
    A couple π-related trivia bits I picked up recently from watching BBC “history of maths [sic]” vids on YouTube.

    Apparently, the Sumerians worked it out to four digits a millenium or so before Archimedes — assuming that the documentarians are telling me the truth about cuneiform numbers. They showed a clay tablet with angles and arcs and everything!

    Also apparently (because I saw this in a doco and don’t have handy links), there was a student of Pythagoras working on π, and he confided to a classmate that he didn’t think there was an integer ratio that would exactly represent π. Because Pythagoras had mathematics all confused with religion, and whole-number ratios were the basis of Pythagoreanism, said student was accused of blasphemy and thrown off a cliff and drowned.

    There’s a reason that they’re called irrational numbers; it’s not always pretty.

  2. #2 Childermass
    March 15, 2012

    Three of them are easy. Einstein plus two astronauts with visible name tags. The last one is not hard either if you notice a famous astronomer listed in Wikipedia’s list of people born on March 14.

  3. #3 Ole Phat Stu
    March 15, 2012

    Just FYI : Pi is the ratio of the circumference of any convex curve of constant diameter to that diameter. Usually a circle is stated, but this more precise definition includes e.g. Wankel rotors, and others of that ilk with more than the Wankel’s three lobes :-)

  4. #4 nanonaren
    March 15, 2012

    Pi joke:
    Your mama is so fat that her BMI number is Pi.

  5. #5 Patrick Dennis
    March 15, 2012

    An easier method of determining pi would be to legislate it, as the Indiana legislature supposedly attempted to do in 1897.

    More sensible is the (unfortunately, probably doomed) movement to declare the ubiquitous “circle constant” to be the ratio of a circle’s circumference to its radius, rather than to its diameter. That number, equal to 2*pi, has been given the name tau. The rationale is nicely laid out here: http://tauday.com/tau-manifesto , and lies mainly on the fact that a lot of equations would make more intuitive sense if one trip around a circle equaled one “circle unit” (or tau radian) instead of two “pi radians.” More often than not, when pi shows up in an equation, it is as the term, 2*pi. Supposed exceptions, as in Euler’s equation and the area of a circle, are shown in the manifesto cited above to be more consistent with the tau formulation than with pi.

  6. #6 Greg23
    March 15, 2012

    In the U.S. pi day will be especially significant in 2015.

    3 14 15

    or 2016 (due to rounding)

    3 14 16

  7. #7 cope
    March 15, 2012

    As always, an interesting, stimulating and informative post, thank you.

    I would just like to add a link to a look of the use of dropped toothpicks to approximate pi HERE.

    I’ve always wanted to incorporate this activity into my classes but have never really figured a pertinent way to do so with my earth/space science and astronomy students.

    Maybe some day, just for fun…

  8. #8 Carlos Lopes
    March 15, 2012

    Infinite recursion in “Exclamation point, not factorial!”.

  9. #9 Anonymosity
    March 16, 2012

    I find it interesting how many people obsess over the number of digits they can memorize or utilize. 11 significant figures will allow you to calculate the circumference of any circle that will fit inside the earth to within a millimeter’s tolerance.

    Just for fun, I figured out that 63 sig figs will let you measure the circumference of a circle with the radius of the observable universe to within a Planck length.

  10. #10 Jon Mitchell
    March 16, 2012

    It it true that as one travels closer to the speed of light, the value of pi changes?

  11. #11 ashoka
    March 16, 2012

    it is really interesting, i enjoyed lot,thank you.

  12. #12 Joffan
    March 16, 2012

    No, it’s the flavor of pi that changes near the speed of light. It becomes more… racy.

  13. #13 NSherrard
    March 16, 2012

    To be fair to Archimedes, Zu Chongzhi was not “back then,” he lived 750 years later. That’s not far off the 900 years between Chongzhi and Madhava.

  14. #14 sean t
    March 19, 2012

    Greg23,

    Actually, the most significant pi days were in 1592 (or 1593 if you round). Wonder if anyone noticed.

  15. #15 sean t
    March 19, 2012

    Jon Mitchell,

    Certainly the value of pi does not change when travelling near the speed of light. There would be no length contraction observed in a circle in a comoving reference frame. Pi would therefore have its normal value. In an arbitrary reference frame, length contraction in the direction of motion would render any circle into an ellipse whose eccentricity would depend on the relative speed of the observer’s and the figure’s reference frames.

    What you may be thinking of is in general relativity, there are effects that could lead to observation of a circle which has a circumference to diameter ratio different than pi. This would be the direct result of a change from Euclidean to non-Euclidean curved geometry, however. Since pi is defined for Euclidean geometry, I would think a good argument could be made that this really is not a change in the value of pi, but rather just an alternate geometry.

    Disclaimer: I know just enough about physics and mathematics to get myself in trouble, so I would appreciate anyone who knows more correcting any inaccuracies in my post.

  16. #16 Stephen
    March 28, 2012

    Ok, 3.14. But if “3″ is the month, then .14 of a month gets you to March 4.

    Computer heads use base 8, and pi turns out to be 3.11 in octal.

    They (we) also use base 16, and pi turns out to be 3.24 – handy in case you missed it.

    Tau Day is 6.28. Since that’s 2 * pi, you get to eat twice as much.

    So March 4, 11, 14, 24, June 28, July 22. Lots of pi to eat.

  17. #17 joshua atkins
    136 eagen carkl
    March 14, 2013

    i want to no who ivnent the pi number