Posted by 
“You wait for a gem in an endless sea of blah.” -Lawrence Grossman
On the one hand, we have General Relativity, our theory of space, time, and gravity.
Image credit: Wikimedia commons user Johnstone; Earth from NASA’s Galileo mission.
It describes the Universe on both large and small scales perfectly, from the hot Big Bang to our cold accelerating expansion, from vast superclusters of galaxies down to the interiors of black holes.
Image credit: NASA, ESA, M. Postman (STScI), and the CLASH Team.
But General Relativity doesn’t tell us everything. It doesn’t tell us, for example, about protons, neutrons or electrons. It doesn’t tell us the properties or interactions of matter and energy in the Universe. It only tells you about gravitation: how spacetime affects the matter and energy in it and how the matter and energy respond, gravitationally, to the spacetime they exist in.
But that does include, when an excessive amount of mass/energy gets concentrated in one region of spacetime, black holes.
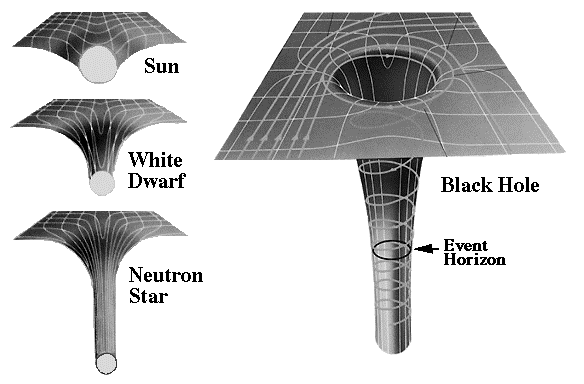Image credit: anrophysics 2008-09, via Bangkok Patana School http://www.patana.ac.th/.
But if you want to properly describe the matter and radiation that lives in this spacetime, you need something else.
You need equations and laws that govern each individual quantum of energy and all of their interactions. You need the Standard Model of Elementary Particles, and all the laws that govern their interactions.
Image credit: The Particle Adventure / CPEP / LBNL.
For that, you need quantum field theory. This is fully relativistic, and is the most complete way we have of describing the interactions of all matter, energy, and fields in the Universe.
It’s incredibly complex, but it’s calculable using a variety of techniques.
Image credit: Michele Vallisneri, Ira Rothstein and Chad Galley, using an EFT.
The problem — and the source of many paradoxes — is what happens when we try to put General Relativity and Quantum Field Theory together. Because we don’t have a quantum theory of gravity, this typically means using General Relativity to figure out how the background spacetime is configured, and then using Quantum Field Theory in that curved spacetime to figure out the nuances of how that particle behaves.
I’ve done exactly one calculation of QFT in curved spacetime in my life (the one to derive Hawking radiation), and it was one of the most difficult calculations I’ve ever done.
Image credit: John Baez, Nature 421, 702-703 (13 February 2003).
Recently, another paradox has emerged that you might have heard of: that of Black Hole Firewalls.
Image credit: NASA / JPL-Caltech.
If you fall in towards a black hole, you wouldn’t notice anything special other than the gravitational redshifting of light and the increasing gravitational tidal forces as you fell in.
As you got close enough to the event horizon, you’d pass through ISCO, or the innermost stable circular orbit, interior to which there would be no matter or radiation. The black hole eventually swallows your field of vision, and into the event horizon you go.
Image credit: Andrew Hamilton, who has some great visuals at http://jila.colorado.edu/.
According to standard General Relativity, nothing funny or fancy should happen to you as you cross the event horizon, just the same small increases in tidal forces as you continue to approach the singularity.
But the “Firewall paradox,” discovered last year, appeared to show that an intense firewall of radiation existed everywhere at once along the event horizon in a large black hole, and would incinerate anything or anyone that attempted to cross in horrific fashion.
Image credit: lordphenix2002 of photobucket.
Here’s the thing: when two quantum systems are entangled, you can know the properties of one particle by measuring the properties of the other. For example, I can entangle two photons so that one has spin +1, and the other has spin -1. If I measure the spin of one, I immediately know the spin of the other. But if I don’t measure the spin of either, they both remain undetermined.
The paradox comes about when you have two entangled particles, and one – but not the other — falls into the black hole.
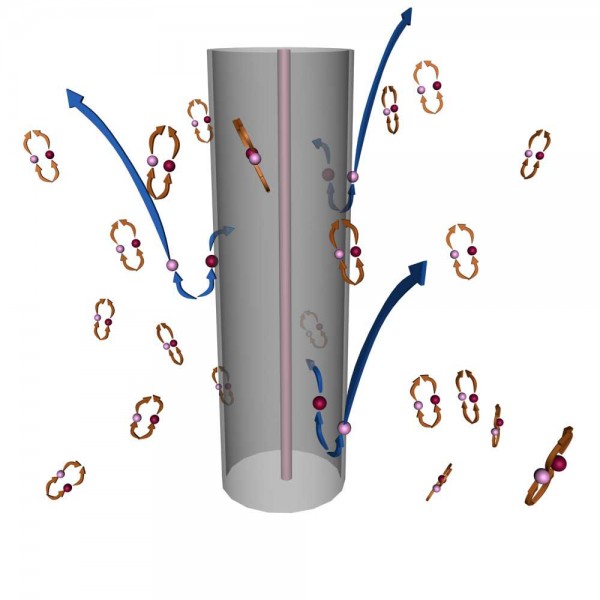Image credit: Oracle Thinkquest, via http://library.thinkquest.org/.
If you break the entanglement, by say, measuring the properties of the one that didn’t fall in, a barrier of energetic particles would descend around the event horizon of the black hole; that’s where the alleged firewall comes from.
At least, that was the paradox, as it was stated last year. But three physicists that you’ve probably never heard of – Samuel L. Braunstein, Stefano Pirandola, and Karol Życzkowski — have come up with the resolution here!
Image credit: Braunstein, Pirandola and Z˙yczkowski, Phys. Rev. Lett. 110, 101301 (2013).
The fun thing that they found, here, is that the greater the entanglement across the event horizon of the black hole, the later the firewall curtain falls. More entanglement = more time.
So you’d think that this would be good for large black holes and bad for small black holes, naïvely, and this could have been the case. But in our Universe — as this paper shows — entanglement across all black hole event horizons is maximized, which means that the time it takes the firewall curtain-to-fall is… infinite.
Image credit: Sabrina Herbst of Penn State.
In other words, entanglement is maximized and the black hole firewall never forms.
So you won’t get fried as you fall into a black hole, even if you wait an arbitrarily long time. You can wait and wait and wait all you want, but infinity never comes.
Image credit: Ashley Corbion of http://atramateria.com/.
So when you fall into a black hole, it’s death by spaghettification, not by incineration! And that’s the end of the Black Hole Firewall Paradox!
March 9, 2013
March 9, 2013
March 9, 2013
March 9, 2013
March 10, 2013
March 10, 2013
March 10, 2013
March 14, 2013
March 14, 2013
March 16, 2013
May 8, 2013
