"It followed from the special theory of relativity that mass and energy are both but different manifestations of the same thing — a somewhat unfamiliar conception for the average mind." -Albert Einstein
You've heard and seen it plenty of times: Einstein's most famous equation, E = mc2. I've taken you inside this equation before, which lays out how much energy is stored in matter-at-rest, and tells you how much energy you need to create matter in the first place.
That's right, you can create matter directly from energy; we do it all the time, in fact. In particle accelerators, in stars like the Sun, around black holes and neutron stars, and in cosmic catastrophes, we're constantly creating new matter purely out of energy. It's pretty simple: take two protons with enough energy, smash them together, and you get out three protons and one antiproton. (This is the exact process that used to take place at the old Fermilab accelerator!)
This is how we've made the vast majority of antimatter here on Earth, and if you add up all the kinetic energy of the four particles that come out, you'll find that it's smaller than the kinetic energy of the two protons you started with by exactly... the mass of a proton and an antiproton, times the speed of light squared.
 Image credit: Riken Research of http://www.rikenresearch.riken.jp/.
Image credit: Riken Research of http://www.rikenresearch.riken.jp/.
That's what E = mc2 tells us: that mass is just one form of energy, and that mass can be created or destroyed very easily, so long as you convert that mass into another form of energy. (There are other conservation rules that you may need to obey as well, but you must always conserve the total amount of energy, as far as our experiments can tell.)
But there's a far more common and even mundane application of Einstein's most famous equation: every single nuclear and chemical reaction, ever.
You've heard of a nuclear reaction: it's where we either take lower mass nuclei and combine them to make one or more higher mass nucleus (that's fusion), or we take heavy nuclei and split them apart into lower mass ones (that's fission). In both cases, the amount of energy that comes out is huge, even though the changes in mass are relatively tiny. The most powerful nuclear explosion in history -- the Tsar Bomba -- which released nearly 60 MegaTons of energy, converted less than 50 grams (under 2 ounces) of mass into energy.
The crazy part? When a plant absorbs a photon for photosynthesis, it increases in mass in direct proportion to the energy of the photon it absorbed, following the law of E = mc2. When a human burns through his-or-her chemical fuel in order to maintain their body temperature, they lose mass in direct proportion to the energy released from the breaking of those chemical bonds. In fact, if I did something as simple as weighed a free electron and a free proton on one end of a scale, and weighed a neutral, ground-state hydrogen atom on the other end, I'd find that the free electron and proton weighed more by 13.6 eV/c2, exactly the mass-equivalent of the energy needed to ionize a neutral hydrogen atom!
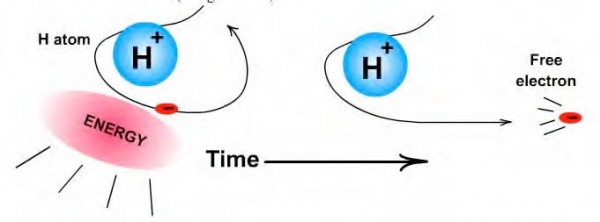 Image credit: Contemporary Chemistry, via http://contemporarychemistry.com/.
Image credit: Contemporary Chemistry, via http://contemporarychemistry.com/.
When you combust hydrogen gas with oxygen gas to make water, it gives off energy, as made famous by the Hindenburg disaster.
Yet the water that's the product of the reaction actually is slightly lower in mass than the hydrogen and oxygen that came before. How much lower in mass? By the exact amount of energy that was released, divided by the speed-of-light squared. (Because if E = mc2, then it's also true that E / c2 = m.)
So every time you do something that releases energy, you're losing mass in direct proportion to the amount of energy that's released.
 Image credit: Greg Schneider Photography, via http://www.gschneiderphoto.com/.
Image credit: Greg Schneider Photography, via http://www.gschneiderphoto.com/.
And similarly, every time you absorb energy, you gain mass in direct proportion to the amount of energy that's absorbed.
So what this means is that mass is a form of energy, and that these two quantities, no matter what you do to a system, are proportional to one another. In terms of an equation, E ∝ m.
But to turn that proportional symbol (∝) into an equal sign, you need to get the conversion factor right. The conversion factor is what tells you how energy is related to mass, quantitatively.
And that conversion factor is the speed-of-light, squared. Figuring all of this out was just one of Einstein's great contributions to our understanding of the Universe.
And that was 108 years ago, already, believe it or not. Even though you probably never think about it, E = mc2 (or E / c2 = m) affects practically everything that occurs in our world; each time you bat an eyelid, flex a muscle, breathe in or out, think a thought or beat your heart, you're converting mass into energy, and each time you digest a meal, you're converting energy back into mass. Everything that adds or subtracts energy from a system causes its mass to change, and we can even figure out, down to the tiniest amounts measurable, by how much.
 Image credit: Stock photo by Matthew Benoit, via http://www.123rf.com/.
Image credit: Stock photo by Matthew Benoit, via http://www.123rf.com/.
How?
Through E = mc2.
- Log in to post comments






The “creation” of a particle antiparticle pair doesn’t occur with every head on proton to proton collision at an energy level above 6 GeV, a level achieved by the Bevatron in 1954. From what I’ve read, only one new proton-antiproton appears in every three million proton to proton collisions at 6 GeV.
The Large Hadron Collider attained an energy level of 7 TeV in 2011, that’s one million times the energy level reached by the Bevatron in the 1950s, yet only one new proton accompanied by one new antiproton, and with a similar relative frequency, is all that still appears per head on proton to proton collision at an energy level one million times higher than that achieved by the Bevatron.
Why only a single pair?
Why only a single pair?
You noted that a proton-proton collision only gives you a newly created proton-antiproton pair in one out of three million tries. The naive way to estimate the probability of creating two pairs is to square the probability of creating a single pair. That would be one out of every ten trillion collisions. I don't know how many proton-proton collisions they have actually done, but it may be that they haven't done enough to detect the double-pair-creation pathway at the customary 5σ level. IOW, I don't think that double-pair creation is forbidden, but it is so rare that you would need to be working at a precision of about 13 decimal places to worry about it.
It should probably be noted (in case in isn't obvious from the tiny mass converted in the Tsar Bomba) that the amount of mass gained or lost by these processes is NOT the pounds or kilos that show up on one's bathroom scale.
BenHead: Lol, yeah. I find it really funny when people say they don't believe normal chemical reactions etc. result in mass changes because they can't see the change on whatever scale they happened to use which was at best a college lab scale with a few digits of precision. Everyone knows that E=mc^2 means there's a lot of energy tied up in matter, but somehow the reverse doesn't occur to them.
Also, I'm trying to get away from using the "conversion"-type terminology that suggests mass is a "kind" of energy, and instead say what it really is: Literally the same thing in different units. *Matter* is a type of energy. Mass is energy.
Does the same relationship hold between the mass of dark matter and dark energy? (What I've read seems to imply that we don't see conversions between normal x and dark x; so I'm wondering whether they obey very different kinds of laws.)
Bill: Yes. Whatever Dark Matter is -- even if it's not a new type of particle but some other phenomenon -- if it has energy, then it has mass, because they're the same thing just with a c^2 unit conversion factor. Assuming it is a particle, and that it might annihilate when it interacts, we should (eventually) be able to see signs of this and the energy of the radiation we see will let us figure out what the mass of the dark matter particle is. There are experiments looking for this right now.
Dark Energy would also follow the same rule, and the mass of the universe is 4x bigger than it would be without DE. It's weirder with DE because the kind of energy it is has an effect that's different from what you expect from "normal" mass (where normal in this case includes dark matter).
But E=mc^2 always holds.
Nice article. Nice to hear mention of the mass of the ground-state hydrogen atom being less than the mass of the separate proton and electron. In similar vein when you raise a brick or an electron, you do work on it and give it what's called gravitational potential energy. This is in the brick/electron. Its mass increases. When you drop it, it's converted into kinetic energy. Once you've dissipated this, the mass is reduced. Invariant mass varies! Oh by the way, the Higgs mechanism contradicts E=mc². This is worth a read: http://www.tardyon.de/mirror/hooft/hooft.htm . NB: it's not THE 't Hooft, it's some other 't Hooft.
No, the Higgs mechanism does not contradict E=mc^2. It (like everything else in modern physics) depends on it being true. It is the potential of a particle wrt the Higgs field that results in them having rest mass. Guess what the proportionality constant of potential energy to mass is?
Also, potential energy is stored in the field. If you lift a brick, the gravitational potential energy is stored in the gravitational field between it and the earth. Therefore you only see the additional mass if you consider the whole earth/brick system. If this was not the case you'd have the question of why the potential energy isn't stored in the earth when it, too, had its potential wrt the brick increased by the same amount. The potential is between the two. The system as a whole is what has increased energy, and therefore mass.
CB: the mass of a body is a measure of its energy-content, not a measure of its interaction with a cosmic-treacle field. And the gravitational potential energy is in the brick. If you give the brick 11km/s worth of potential energy it escapes the system. A brick "at rest" in free space has more mass-energy than the same brick at rest on the ground. You know this because when you throw a 1kg brick into a black hole, the black hole mass increases by 1kg. Just before the brick disappeared into the black hole it had considerable kinetic energy, but the "relativistic mass" or total energy of the fast-moving brick was still 1kg.
As always, an interesting read. But.
"So every time you do something that releases energy, you’re losing mass in direct proportion to the amount of energy that’s released. And similarly, every time you absorb energy, you gain mass in direct proportion to the amount of energy that’s absorbed."
Not true.
State changes. Crystal structure change. There is a delta E for each, and there is no associated change in mass in these processes. For example,when water turns from liquid to gas.
Also, any given chemical reaction is going to have delta H's for the making and/or breaking of bonds. There does not need to be a correlating loss or gain of mass for there to be a change in energy (which is either released or absorbed).
@ Eric Lund
Here’s a link to an article on the proton-proton collisions at the LHC. From the first paragraph:
http://www.newswise.com/articles/lhc-proton-run-for-2011-reaches-succes…
Newswise — Geneva, 31 October 2011. After some 180 days of running and four hundred trillion proton proton collisions, the LHC’s 2011 proton run came to an end at 5.15pm yesterday evening.
That’s forty times the square of the frequency you mentioned in post #2 and does not take into account the trillions of proton to proton collisions that took place previously.
"CB: the mass of a body is a measure of its energy-content, not a measure of its interaction with a cosmic-treacle field."
Wrong.
Mass is defined by its resistant to change in motion.
There's nothing in the "energy content" that would bring that about, but there IS something about an interation with a Higgs field that WOULD bring that about.
Please stop telling people who are right that they are wrong and in doing so making a complete and utter arse of yourself, it wastes my time correcting your asinine mistake and confuses people who know more than you but not enough to know you're talking bollocks.
Alan, there was nothing there about the rate of pair production there, never mind the rate of pair production, so unless you're trying to say Eric overestimated the rate of this (which was based on the proviso that the figures *he* had been given were accurate, so complaining to HIM about the error in calculation is entirely uncalled for) or you're missing a hell of a lot of information there and therefore have nothing to make the condemnatory implication valid.
(remove the "or", in ") or you're missing", the sentence lasted longer than my short-term buffer).
"State changes. Crystal structure change. There is a delta E for each, and there is no associated change in mass in these processes"
Not in actual fact.
The condensation of a gas to a liquid will cause a loss in **MASS**. As will reorganisation from one crystal lattice of Diamond to the energetically favoured graphite will also cause a loss in mass.
That would be then lost to the system by, for example, the heating of the resultant and the loss of that heat energy as photons to the surround, meaning that the mass would not be there to be calculated any more.
Weighing the element "fire" was easy in comparison to this change in mass, however.
@ Wow
I was not “complaining to HIM” about anything.
Piss off, you obnoxious fuck.
Postulaatide absolutiseerimine (erirelatiivsusteoorias) ja "lihtsa" valemi E = mc^2; "materialiseerimine - koos mõlema kooskõlastatult kuulutamisega HEURISTILISTEKS - see on, mis on takistanud juba pärast II Maailmasõda Füüsika edasiarengut. Loomulikult on seda abrakadabrat süvendanud mass/osakeste duaalsuse "lubamine" + osakeste ristlainetus "mittemilleski".
1. "Väike viga": Lorentz-teisenduste`le bijektiivse kuju andmine, mis viib (alati!) väärale arusaamale: vastandteisendustest kui pöördteisendustest (teisenduste endi nii multiplikatiivsel kui ka additiivsel kujul?).
Keelelis-intuitiivselt: "Einsteini rongi" Pikkust mõõdetakse peegelteisendusega (POSTULEERIDES geomeetrilise keskmise teisendusfunktsiooni f*(ct) = f(+)(f(-)) = k - olemasolu!?)
2. Valemi E = mc^2 õigsuses pole vaja kahelda, KUID milleks "kaotab" selline energia/massi (vrdl. osake/laine!?) kokkukleepimine - KEHADE VÄELISUSE?
VÄGI = mistahes monaadse keha võimelisus subjektsuseks relatiivses liikumises (ka: teisenenud ruumi MÕÕDISTAMISEL). VÄGI - ei ole (otseselt?) materiaalne mõiste, kuid (kasutades kaugmõju printsiipi!) - on nimelt VAIMSE VÄE primaarsuse-nõue!
Ettepanek:
Mingem "veidi" tagasi - Galilei teisendusteni erirelatiivsusteoorias; ja "edasi" - üldrelatiivsusteooria subjektsuse määratlemisega!
Tänan tähelepanu eest!
Then your post was that of a flailing moron you impotent twat.
@ William:
"State changes. Crystal structure change. There is a delta E for each, and there is no associated change in mass in these processes. For example,when water turns from liquid to gas."
Yes there absolutely is, whenever there is a change in energy. However that change in mass is equal to delta-E/c^2. Ergo it is very small. Most of the time, therefore, you can ignore it, because you can't even measure it (i.e. on your college lab scale). That doesn't mean it doesn't exist, and can never be measured. It can.
'MegaTons of energy' might confuse some people. Need to put the TNT reference in.
As you point out, it was actually just 50 grams of energy.
John Duffield: Still hanging your hat on your completely wrong description of a brick falling in a black hole, I see. Good job ignoring the paradox inherent in this incorrect view: Why is the extra mass-energy stored in the *brick* and not the *earth*? The earth's potential with respect to the brick increased by the exact same amount! So did the earth's mass also increase by the same amount, violating the Conservation of Energy that you love but don't understand? Or did each get 1/2 the mass, or some other proportion? Or did you just not think about this and that's why you're wrong?
Fields can store energy. Electric potential energy is stored in the electromagnetic field between two charged objects, just like gravitational potential energy is stored in the gravitational field between the brick and earth, or brick and black hole. It's not "in" either object, so weighing them both separately, then collectively after you let them fall together, will show a net increase equal to the gravitational potential energy that was present before. Only if you weigh the entire brick-earth or brick-BH SYSTEM before hand will you see no mass change.
The idea that energy can only be stored in "objects" is a supremely naive view. This is especially obvious when considering that what you call a "brick" is, itself, just particular kinds of energy stored in various fields.
John Duffield: "the mass of a body is a measure of its energy-content, not a measure of its interaction with a cosmic-treacle field."
Because field potentials aren't a type of energy. Got it. "It" being how ignorant you are.
"However that change in mass is equal to delta-E/c^2. Ergo it is very small."
I literally woke up today thinking exactly this, and realized why it would be something ignored by University Chemistry. I do feel slightly cheated though. I suppose P-Chem is already hard enough, but still... should I ask for a refund?
William: Heh, good on you!
It certainly would be nice if they'd at least mention how E=mc^2 applies but that you'll be ignoring it for the rest of the semester because the change is so small. Kinda like it'd be nice if they'd mentioned that the model of the atom du jour was just an approximation or outdated model, but enough for now.
John Duffield,
Think of it in terms of work and use the relativity principle: (let m be the mass of the brick, M the mass of the earth, and r be their separation)
From a reference frame in which the earth is stationary, if we raise the brick to height r and let it go, the force exerted on the brick is GMm/r^2. The brick travels through a distance r (assuming for simplicity that the earth and brick are point masses, which does not affect the conclusion). Therefore the earth does work equal to GMm/r on the brick and the brick must increase in mass by GMm/(rc^2). The earth has done work, so its mass must decrease by the same amount. If the brick stops moving and dissipates its energy in some other form, its mass decreases by this amount also, meaning that the earth/brick system's mass has decreased by GMm/(rc^2), the mass equivalent of the gravitational potential energy.
Treating the same situation from a reference frame in which the earth is moving and the brick stationary:
The brick exerts a force GMm/r^2 on the earth. The earth moves through a distance r. The brick therefore does work GMm/r on the earth. The earth's mass therefore increases by GMm/(rc^2). The brick has done work and its mass must decrease by this same amount. Assuming the earth stops moving and dissipates its energy, its mass decreases by this same amount, again leading to the conclusion that the total mass of the system decreases by GMm/(rc^2).
These are both physically equivalent and equally valid descriptions of the process. The only point of agreement they have WRT the mass is that the total mass of the system decreases by GMm/(rc^2) once the components have stopped moving. Therefore, the only absolute thing we can say is that the system gains mass when the components are separated and loses mass when they are brought together. We cannot say in physically valid absolute terms that the brick gains mass when the earth and brick are separated; it's equally valid to say that the mass of the brick remains unchanged and that the mass of the earth increases in that situation.
So 1 kilogram water has more mass than 1 kilogram ice ?
Sean: with respect, your description is incorrect. You do work on the brick when you raise it. The Earth doesn’t do work on the brick as it falls. There is no magical mysterious mechanism by which the Earth loses mass to a falling body. Gravity is not a force in the Newtonian sense. Yes when you dissipate the kinetic energy of the falling brick its mass decreases, but its mass increased when you raised it. It isn’t valid to claim symmetry between the brick and the Earth. Imagine you raise the brick using an explosion which exerts equal and opposite force on both the brick and the Earth. They each acquire the same |p|=mv momentum but the KE=½mv² is not shared equally. The brick gets the lion’s share of the kinetic energy. If that explosion is sufficient to give the brick an 11km/s escape velocity, the brick takes that kinetic energy away with it, and it's never coming back. It’s lost to the system.
CB: I'm not wrong about this. Go and find a relativity expert. He will confirm that I'm right.
"with respect, your description is incorrect. You do work on the brick when you raise it. The Earth doesn’t do work on the brick as it falls."
With all due respect, that's a load of gobshite, John.
M: "gram" is a unit of mass, unlike "pound" which is a unit of force. So if you freeze a kilogram of water you end up with less than a kilogram of ice.
Hope I got that right. It's getting to where it's worth your clean shirt to make a comment or ask a question in here any more. No wonder Ethan doesn't stick his head in that often. Jezzus, people.
@ M
the density of ice and water are not the same. And since there is a relation between mass, volume and density.. your question needs some refining, because not all of those 3 properties will be the same for 1kg of water and ice.
p.s. it depends what you are getting at. Mass on it's own doesn't exist. It is always connected to some force or other physical property.
If you just speak of weight.. than 1kg of anything is same to 1kg of anything else.. that's what weight is.
Sinisa: what Marshall said sounds right to me. In his E=mc² paper* Einstein said a radiating body loses mass. So your 1kg of water radiates away its heat. So when it's turned to ice, its mass is slightly less than 1kg. The same applies if you drop a 1kg brick and radiate away the kinetic energy.
* http://www.fourmilab.ch/etexts/einstein/E_mc2/www/
@ 34 John
your reply is exactly why I said "the question needs refining".
There are other things that need to be taken into consideration. You approach it from E=mc^2, but there are many different ways in which mass relates.. i.e. through volume and density, momentum and velocity, relativity etc..
You introduced radiation as an additional element in the system. So it's not just 1kg of two things. There is an additional element. And so on...
You, or rather "M" needs to specify the parameters. Is it at room temperature, is it a closed system, are there, and what are the forces acting upon it.. etc. etc.. Without all that 1kg of ice has the same mass as 1kg of water. 1 kg of water will not make 1kg of ice. That's another thing. But if you already have 1kg of each.. their masses, strictly speaking are same... 1kg
John,
With all due respect, please learn some basic high school level physics before you come on here and spout your crap. Work is defined in physics as occuring when a force acts on a body and that body moves in response to that force. In equation form W = F dr, where F is the force vector, dr is the change in the position vector, and the product involved is the standard dot product (sorry I couldn't properly render the "dot" on here). When you lift a brick, you certainly must exert a force on it, and by definition since you are lifting it, it moves in response. Therefore, as you correctly recognized, you do work on the brick when lifting it. Now, why does it fall? It falls because the earth exerts a force on it. When it does, the brick moves in response. Therefore, the earth does work on the brick when it falls, just as I stated.
John,
Further, while this description seems counterintuitive and unfamiliar, it is physically valid. The brick does work on the earth when the earth falls toward the brick. It is perfectly valid to consider a reference frame in which the brick is stationary and the earth moving. Further, Newton's gravitational law (which is certainly valid in the weak field of the earth-brick system) is symmetrical. The earth exerts a force on the brick, but the brick exerts the same force on the earth. Therefore, the brick is exerting a force on the earth, and the earth moves in response. Thus, the brick does work on the earth in that reference frame.
http://scienceblogs.com/startswithabang/files/2013/07/binding_energy.gif
Binding energy is negative. 1.74 solar-mass 465.1 Hz pulsar PSR J1903+0327 has -15.3% binding energy. it masses 15.3% less than its unbound summed baryonic composition (AP4 model). Fusion is much more efficient for releasing energy, absolutely per mole and especially per gram.
" Tsar Bomba...converted less than 50 grams (under 2 ounces) of mass into energy." The number of Tsar Bomba electrons, protons, and neutrons immediately pre- and -post-detonation were identical. The immediate energy release was reshuffling nuclear binding energies. Neither fission nor fusion immediately transforms or destroys electrons, protons, or neutrons. Daughter decays then follow, that do. Russians boasted of a lead bomb jacket (inerital confinement), leading to the cleanest nuclear detonation re fallout. A depleted uranium jacket would have given 100+ megatons and planet-searing fallout. However... Each D-T fusion emitted averages 1/2 neutron. That astounding neutron blast did N(14) + n to C(14) + p, adding a huge load of carbon-14 into the world.
It is proven by Chou et. al., 2010 that your head ticks faster than your feet. Using atomic clocks. But you can substitute one elctromagnetic process for any other. So what is the case for a faster oszillating field? It contains more energy = more mass. This is the case at your head. Mind you incoming and outgoing light is a different issue because it has to fight the potential when leaving, we however lift our head up and thus do work.
So for a brick falling, it looses energy/mass - and of course this doesn't get lost but remains contained within the field. It is well known that when two objects come together they have a combined lower mass than the two on their own.
So I think this energy/mass difference getting returned to space into the grevitational field is correct.
So I agree with you Wow (or CB?). But why are you so unnice to people. Why trolling on someone's blog and abusing others rather than guiding them with provision of facts if you are that superior? They might not know better and be greatful for facts and evidence. I sometimes get things wrong but always change my opinion when I see new facts.
I read you little passage about DM here and you might be surprised to find that my hypothesis which comes up with the 83.44% invisible, realy bases on not much else but E=mc^2 ... applied to something that I thought had been neglected ... good luck catching any radiation though...
I just had to make a late comment to this thread. I appreciated Ethan writing it. This concept of mass varying with total energy content is something I encountered a few months ago. I thought it was an error at the time and was startled when someone casually affirmed it, like it was obvious.
Before I fully accepted it I wanted to a reasonably reliable source reinforcing it. I guess this qualifies. And as a bonus, a question I had about the ramifications of this has been answered in the comments. That mass will change if you lift something off the ground.
I'm still really annoyed. I was taught specifically that E=MC^2 only described nuclear reactions. It's not that no one ever said anything about chemical reactions, I was specifically taught in science classes that mass does not change in chemical reactions. Now I find out that this is wrong, and it was known to be wrong at the time.
I get that the total change is impossibly small, but that's not the point. The point is that not only was I not told all there was to it, I was taught the wrong things in a class that was supposed to be informing me about the nature of reality. I feel pretty angry and betrayed, I liked my science classes, I enjoyed learning about that kind of thing. The idea that I was working to learn things that were wrong leaves me feeling almost violated.
Incidentally they screwed up evolution too. Yep, all I got was the trite "random mutation plus natural selection equals evolution" picture. Not a single word of neutral drift. Pure adaptionism. I've spent years trying to correct the false assumptions that had me making. It's going to take quite a while before I really have accepted that a chemical reaction can alter mass as well. It's still ingrained in me, the idea that nuclear reactions are special because they translate mass into energy. That chemical reactions specifically cannot do that. Unlearning that is not going to happen fast.
Please examine the latest publication on Einstein's equation:
M.A. Padmanabha Rao, Discovery of superluminal velocities of X-rays and Bharat Radiation challenging the validity of Einstein’s formula E= mc^2, IOSR Journal of Applied Physics (IOSR-JAP), .Volume 4, Issue 4 (Sep. - Oct. 2013), PP 08-14 DOI: 10.9790/4861-0420624
http://www.iosrjournals.org/iosr-jap/papers/Vol4-issue4/B0440814.pdf?id…
Abstract: The current paper reports discovery of superluminal velocities of X-rays, and Bharat Radiation in 12.87 to 31 nm range from solar spectra. The discovery challenges the 100 year old Albert Einstein’s assertion that nothing can go faster than velocity of light c in vacuum while formulating E = mc^2 in his special theory of relativity reported in 1905. Several solar spectra recorded at various wavelengths by Woods et al in 2011 demonstrated GOES X-rays arriving earlier than 13.5 nm emission, which in turn arriving earlier than 33.5 nm emission. Finally, the investigators faced difficulty in concluding that short wavelengths traveled fast because of lack of information whether all the three emissions originated from the same source and at the same time. Very recently the author has reported GOES X-rays (7.0 nm) cause 13.5 nm (Bharat Radiation), which in turn causes 33.5 nm Extreme ultraviolet (EUV) emission from same excited atoms present in solar flare by Padmanabha Rao Effect. Based on these findings, the author succeeded in explaining how the solar spectral findings provide direct evidences on superluminal velocities of GOES X-ray and 13.5 nm Bharat Radiation emissions, when 33.5 nm EUV emission is considered travelling at velocity of light c. Among X-ray wavelengths, the short wavelength 7.0 nm X-rays traveled faster than 9.4 nm X-rays, while X-rays go at superluminal velocities. Among Bharat radiation wavelengths, short wavelengths showed fast travel, while Bharat Radiation goes at superluminal velocities as compared to 33.5 EUV emission.
- for all who enjoy a good Sherlock Holmes and Dr. Watson yarn. How they discover who really came up with L=mV² (E=MC²)
First review, from Serbia: http://inserbia.info/news/2014/01/sherlock-holmes-and-the-mystery-of-ei…
Sherlock Holmes And The Mystery of Einstein's Daughter by Tim Symonds