"For the wise man looks into space and he knows there is no limited dimensions." -Lao Tzu
You know the deal: it's the end of the week, so it's time for another Ask Ethan! You've continued to send in your questions-and-suggestions, much to my delight, and I'm pleased to tell you that this week's question comes from Peter Tibbles. Peter asks about obtaining information from beyond where Einstein's theory of relativity allows us to see:
Because of the expansion of the universe there is an event horizon beyond which we can know nothing. There’s been one instance of intelligent life evolved (us); let’s assume another in a galaxy far, far away. They have the same size event horizon (that includes us). On the “other side” of them (away from us) they would be able to see parts of the universe that’s beyond our event horizon.
Now, they see something there and say “That’s interesting, let’s share it with everyone”. So, they send out signals about this. We pick them up and decode them (we are theoretically intelligent). Thus we would be able to know something of features beyond our event horizon. [...] Is this theoretically possible, or have I made a blunder somewhere?
This is a really interesting possibility Peter has brought up! Let's walk through what he's asking.
Image credit: Wikimedia Commons user Azcolvin429.
On the one hand, we can -- if we're clever -- look back all the way to the beginning of our Universe, at least as it can first be described by the Big Bang, some 13.8 billion years ago. We have direct images of the Universe from when it was just 380,000 years old (of the Cosmic Microwave Background), below...
Image credit: ESA and the Planck Collaboration.
and we can see stars and galaxies from nearly that long ago as well, up to the limits of modern telescope technology. The current record-holder's light is just reaching us now after a journey of 13.4 billion years, placing it an unbelievably large 33 billion light years away, a record that will only be broken once the James Webb Space Telescope comes online in a few years.
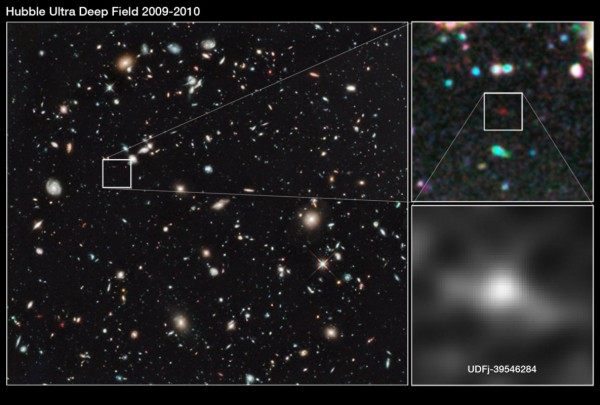Image credit: NASA, ESA, G. Illingworth (University of California, Santa Cruz), R. Bouwens (University of California, Santa Cruz, and Leiden University) and the HUDF09 Team.
The thing is, we're limited by the part of the Universe that's observable to us. Since the Big Bang, light has been on a journey for up to 13.8 billion years, which means we can see the light that's traveled for up to that long in any direction we look.
But that doesn't mean there isn't more Universe beyond that; in fact, we're sure there is, and the only question we have is how much!
Image credit: Rob Knop of Galactic Interactions, via http://scientopia.org/blogs/galacticinteractions/2012/02/27/the-minimum….
Now, here's where Peter's question comes in. If there's a limit to what we can see, then that limit must be the same for the observers whose light we're seeing!
In other words, if we look at two galaxies in opposite directions, both of which have had their light traveling for, say, 13.7 billion years, we can see both of them, but they can't see each other.
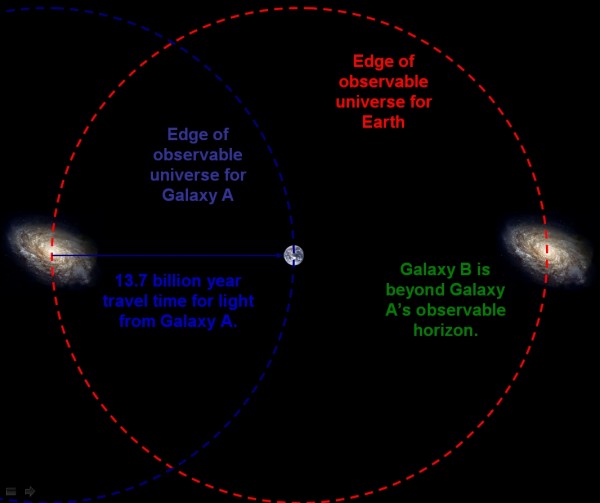Image credit: The Scientific Gamer, via http://scientificgamer.com/inflation-theory/.
And if there's an intelligent person in either one of them, couldn't they send us information about the things they've seen that are inaccessible to us, therefore "cheating" the limits of space and time, and giving us information about the Universe that we wouldn't have otherwise?
It's a fun question to ponder! After all, wouldn't we be doing that exact thing if, say, we sent an image of the Hubble eXtreme Deep Field to a galaxy in the complete opposite direction of us?
Image credit: NASA; ESA; G. Illingworth, D. Magee, and P. Oesch, University of California, Santa Cruz; R. Bouwens, Leiden University; and the HUDF09 Team.
Or, for that matter, a map of the large-scale structure of the Universe as we see it? And, for that matter, couldn't we keep passing that information on and on and on, learning about the Universe far beyond what any one observer, on their own, could see?
Image credit: Zosia Rostomian, Lawrence Berkeley National Laboratory.
It's a remarkably tempting thought, but -- unfortunately -- it's a flawed line of thinking. Can you spot where it goes wrong?
I'll give you a hint: think about the light that we can see from something extremely far away.
Yes, it's a fact that distant galaxy is emitting light right now, 13.8 billion years into our Universe. But we'll never receive it.
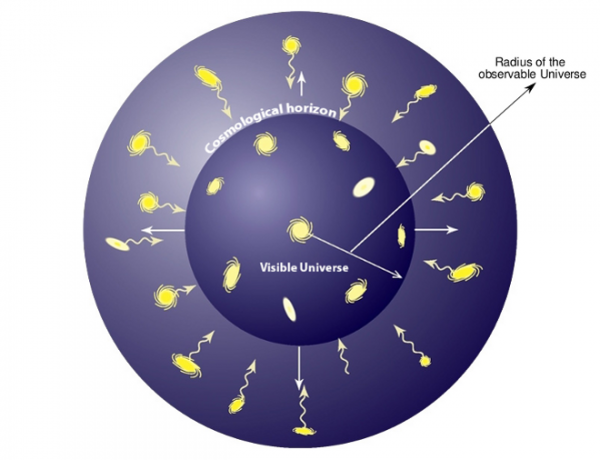Image credit: dournac.org © 2003 by fab, via http://dournac.org/info/size_universe.
You see, not only is the Universe expanding, but that expansion is accelerating thanks to dark energy, and light emitted from galaxies beyond a certain distance will no longer reach us.
If it weren't for dark energy, we would eventually be able see that light (and receive that information) they're sending today... but only at-or-after the light from those galaxies they observed would have reached us anyway.
![Image credit: Wang, Yi; arXiv:1303.1523 [hep-th].](/files/startswithabang/files/2014/02/fig_horizon_problem.png)
Image credit: Wang, Yi; arXiv:1303.1523 [hep-th].
So yes, we can "get information" from objects that are beyond our apparent horizon today, but only once they move inside our horizon in the first place. And because of dark energy, everything that's ever going to be inside our apparent horizon is already here!
Thanks for a great question and I hope you enjoyed the fun answer; keep sending in your questions and check out the week you missed over on Medium; there are some great ones!
- Log in to post comments
More like this
I don't understand....if we all started at the same spot (Big Bang) and can only travel as fast as the speed of light, how do we look back and say that x lights yrs away.
Bruce, because inflation moved points that were very close together apart at a rate faster than the speed of light.
@ Steve. The inflation did not move points at a rate faster than the speed of light. No, no, no. The inflation shaped the space-time continuum faster then the speed of light. There is no known limit to with which speed space-time can change. And there probaly is no limit. Never aproach a problem te Newton way.
Great explanation, Ethan. I had a simpler thought, myself: assuming that any information transmitted by said distant intelligence was also limited to the speed of light, it would take 13.7 billion years to reach us, thus not really giving us any useful information (about the present, anyway...and not "us," per se, but rather our descendents).
If they possessed some sort of instantaneous communications method, then I suppose that would be different.
The Medium site blows, sorry. No comments, twitter account required, no thanks. You should post everything here that you do there.
How do traffic numbers compare?
Agreed with #5. I can't have a Twitter account for work-related security reasons, so no Medium for me either.
Cross-check on spacetime expanding faster than c: As the universe expands, objects we can presently see will become invisible.
So, we are not expanding our universe boundaries as stuff gets farther and farther away in an expanding universe. Instead, simply, stuff will still be there, but be just be too far away for us to ever see...or know where it has gone... but it's still there, somewhere beyond our view/horizon... but some other entity may be able to see it, or...
Possibilities.
Never-ending questions.
What if you had a taught rope that was 27 billion light years long and pulled it... would the other end never react due to the expansion of the universe?
@ Julian
it would reach because the forces holding the rope are.. well, holding the rope. Only gravitationaly unbound object are moving away from one another.
What Ethan is saying is that whatever "snapshot" someone out there sends you... by the time that info reach you, your horizon would have expanded to encompass that info anyways.
It seems to me that even in a static universe, the limits of information given by relativity still apply. Consider, in a static universe, we would have a horizon limit of 13.8 billion light years. That would be the same for all observers. However, this horizon would expand at the speed of light for all observers. If we see an object in one direction that is 13.8 billion light years distant and then broadcast that image to an intelligent observer 13.8 billion ly distant in the opposite direction, it would take 13.8 billion years for that observer to receive the image. By that time, the horizon for all observers would be 27.6 billion light years. The object whose image we sent would then be within the observable horizon of the recipient.
Sinisa, I would think the answer to Julian's question is that taught ropes are not allowed in relativity, because tugging on the rope would send a signal faster than light. I think this is similar to a thought experiment in a book by Wofgang Rindler where a pole vaulter was able to store a 20' pole vaulting pole in a 10' deep garage by running into the garage at .866c. In the garage frame the pole was 10' long so it fit into the garage. The pole vaulter would quickly close the garage door. But in the pole vaulter's frame when he was running the garage was only 5' deep! Rindler explained that a rigid object is not possible in relativity.
@ John
I think you misunderstand the question and answer. And what you write about ftl and ropes and relativity just doesn't make sense.
"Rindler explained that a rigid object is not possible in relativity."
really? And what is earth and sun and all else if not rigid?
Julian asked if in an EXPANDING universe a tug on the rope would ever reach the end of rope. He hints that rope would also expand. I and I answered that it wouldn't, and the tug would reach the end of the rope in some finite time. The rope doesn't expand with the expansion of spacetime since the atomic forces within the rope are much stronger than expansion.
@Sinisa #12: John's comment left out an important adjective. It is a true statement that _infinitely_ rigid objects (e.g., the "ideal rods" you encounter in physics homework problems :-) are incompatible with relativity.
The "ladder paradox" John mentions isn't relevant to this issue, of course; the rigidity argument relates to the thought experiment of swinging a stick. If you swing a stick 1 m long at an angular speed of 1/6 of a revolution per second (so 60 degrees, or about 1 radian, per second), the far end of the stick is moving at 1 m/s. If you make that same (ideal physics homework) stick 1 km long, and swing it at the same angular speed, the far end is moving at 1 km/s. Now make the stick as long as the distance to the Moon (400,000 km) and pivot it at 1 rad/s: the far end sweeps around faster than the speed of light. Impossible!
Yes, impossible. Because in fact, when you swing the rod in real life (and this applies even to the kilometer long verson, or even a two or three meter long one) the whole thing does NOT swing as a unit. Instead, your pivot induces a transverse impulse, which propagates along the rod at the speed of sound for the material, until it reaches the far end, and that end moves. For steel, that propagation speed is about 6 km/s, so we never see or notice the effect. Also, if your pivot is too large, the propagating impulse will exceed the strength of the material along the way, and the rod will break.
The same argument from relativity applies to ropes with perfect elasticity and tension. Your own argument was not related to relativity, and is quite correct in asserting that a long rope would not locally be broken or stretched by the cosmological expansion.
It is, however, a very interesting thought experiment to ask what would happen to a solid material object with a cosmological length scale. It raises some serious Machian questions about simultaneity and mutual rest frames, and whether such an object could actually be constructed in an expanding Universe.
The idea itself, that you have infinitely strong rods breaks causality, since the information has to pass from one atom to the next along the entire length of the rod instantaneously. Or at least fast enough that the speed of motion does not make a deviation of any point along the length away from the force moving it that is noticeable.
So who is surprised when something impossible doesn't appear to work?
However, I don't think it makes much difference here because it's deliberately breaking two paradigms here: intra-atomic forces of tiny scale and cosmic scale are deliberately set against each other, much like the "immovable rock".
When it comes to such a large rod, how did you make it that long? It changes how you decide what it;s going to do because it changes how one end knows things about the other end. Instant creation and one end is not in the light cone of the other and therefore relativistically it is not one body.
Extrude it and you now have to keep in mind that only the force between each element is important and that on cosmological scales the far end won't see the new length produced, therefore why would it be forced on further away from the source by new product?
And the mass. How does it warp space.
Questions left out and ignored by attempting to CREATE a paradox.
Well, just some napkin calculus from wolfram... about our imaginary rope..
let's say that 1km of our rope weighs 1 tone. One light year of our rope would weigh roughly 1/2 Sol. Mass. So, 27 billion ly rope would weigh about 10 billion sol. mass.
It doesn't mean anything.. just thought it would be fun to calculate
@Wow #14: It is an interesting thought experiment, and your own questions point to what make it interesting! I'm not as dismissive as you are, because the conditions of the problem will lead a thoughtful, intelligent reader to some very useful understanding of reality vs. the idealizations we make in physics.
As I see it, the "case of the cosmological rope" is essentially an apparent conflict between local vs. global properties: Let's consider something "realistic" but small enough that it has no appreciable gravitational effect anywhere nearby. Fishing line, or ABS filament, for example.
With a density of 1.04 g/cm^3, 1.75 mm filament has a linear density of 2.5 g/m, or 2.5 kg/km (that's nearly an order of magnitude lighter than Sinisa's rope!). Cosmologically, that linear density is 23.66 billion tonnes per light-year. If it is kept straight, clearly it has no appreciable gravitational effect on its surroundings (the mass of a light year of filament is about 1/1,000th that of a small but interesting asteroid like Apollo!).
If you consider any purely local section of this filament, it is just sitting there quietly, not being cosmologically stretched or anything else. But as Wow said, if it magically appeared in the Universe, then the two ends are causally disconnected!
If instead we "reel it out" through the universe, then that process occurs over a very long timespan (even if we unwind it at some fraction of c), during which the Universe expands around it. How does the filament behave under this scenario? Can we keep it "straight" at all? Can the spool handle an angular rotation fast enough to pull the end at thousands of kilometers per second? How big is the spool, anyway?
If we look at the second scenario (lets call it "reel" scenario). Then it will evolve like any other object.... would be interesting to simulate something like that...
Consider the density of even a thin rope. With a 1.04g/cm^3. That's much more than intergalactic vacuum of couple hydrogen atoms per m^3. So it will "feel" it's own gravity during the time it exists. Even if it started straight "perfect straight" is of course never physically possible. So eventually it will start to twist and turn like giant space worm :) Of course, it will feel any gravity out there also... galaxies, black holes...
And it will compress along its length, that compression being passed as phonons through the solid that transport the forces at the speed of sound in that solid (much slower than light). So extending the reel will produce less and less of a movement of the entire whole as it extends.
The interesting-ness of the questions THAT ARE LEFT OUT are why I'm dismissive of the question *with those questions left out*.
I'm dismissive only because the problem is as poorly posed as the "immovable rock" "conundrum" built to disprove god, or the twin paradox (or the ancient tri-paradox of ancient greece only remembered as the tortoise and arrow), the last being easily solved by including those features elided (e.g. acceleration of only one party).
An infinite sum of a converging series makes it obvious that the arrow will hit the tortoise in finite time.
Interesting is the method by showing a sum of an infinite converging series can occur and result in a finite sum.
So I'm not interested in the partial scenario because it's far FAR less interesting than the elements left out.
Thanks a lot for all the replies to my question, interesting discussion!