“The first principle is that you must not fool yourself, and you are the easiest person to fool.” -Richard Feynman
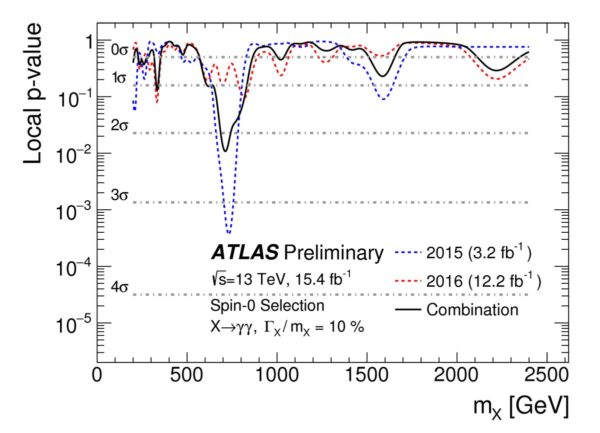
Like many suggestive signals in the past, the 750 GeV bump in the diphoton channel has turned out to be a mere phantasm: an unlikely statistical fluctuation that simply disappeared as more data was collected. While almost the entire particle physics community was hoping for a different outcome, this is apparently the Universe we were dealt.
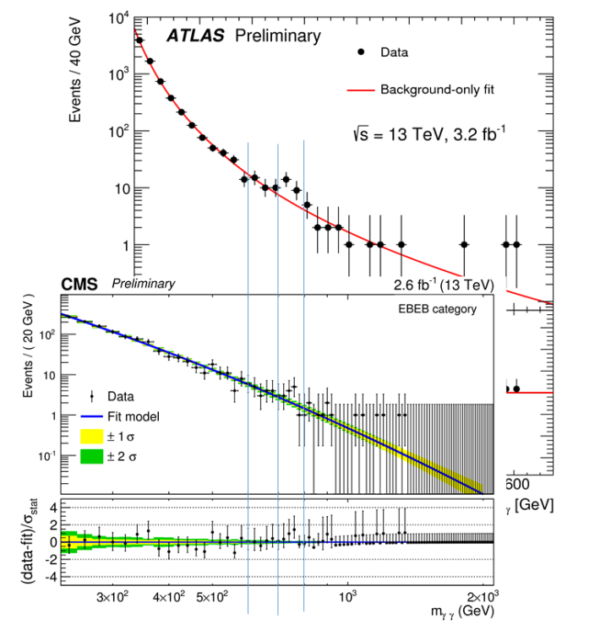The ATLAS and CMS diphoton bumps, displayed together, clearly correlating at ~750 GeV. Image credit: CERN, CMS/ATLAS collaborations, image generated by Matt Strassler at https://profmattstrassler.com/2015/12/16/is-this-the-beginning-of-the-e….
But anyone familiar with the history of particle physics shouldn't be surprised by this result, as "there's only a 1-in-3,000 chance this is a fluke" means there's a *very good* chance that it is, in fact, a fluke. When you flip a coin ten times and get ten heads in a row, you worry that something is wrong. but when you flip a coin a thousand times and get ten heads in a row, you don't.
Image credit: James Beacham for the ATLAS collaboration, via his Twitter account.
That's what happened here. Come get the story and find out how we fooled ourselves!
- Log in to post comments
More like this
If the LHC was creating new particles other than the ones already in the Standard Model, but those particles were sterile, would we know?
In the past I've heard claims that it would be detectable by seeing less mass come out than what went in, but I'm not sure that is true. It isn't one proton being accelerated but rather, at least in the LHC, ~3000 bunches each containing ~100 Billion protons. As the beam and counter beam are crossed you get roughly 600 Million collisions per second.
If you need tons and tons of data to discern statistical flukes from real particles, and sterile neutrinos or other dark matter particles being produced in the collisions weren't interacting with the detectors, would we know? Can we measure how much is going in versus how much is coming out?
@Denier,
"Can we measure how much is going in versus how much is coming out?"
What they're doing is something like making waves in water, the more energy they put into the system the higher the waves and thus the enrgy that comes out of it. But as the energy increases at some point a wave might break. (In fluid dynamics, a breaking wave is a wave whose amplitude reaches a critical level at which some process can suddenly start to occur that causes large amounts of wave energy to be transformed into turbulent kinetic energy.) This is the bumb in the graph of the LHC. The breaking wave is a new particle, a splash, and they can study it what smaller waves, parts, that splash dispers, to study what kind of splash it is. Unless there is no new splash detected there is nothing new.
The question I would like to raise is that when there are ships floating on the water, that as the waves get higher, and far more frequent, that they might get under a lot of strain, as they absorb some of the energy of those waves, and that they would start to splash/break apart?!
@Denier #1: Ignore the nonsensical word salad from #1.
What you really get are 600 million _beam_crossings_ per second. Not every beam crossing results in a collision. The vast majority are simple elastic scatters, where one proton from each beam is deflected at a small angle, but nothing else happens.
Next in line are "minimum bias" events, where two protons collide at a large impact parameter (think "grazing incidence") and you get a spray of mostly pions in a cone around the beam directions.
The really interesting events occur maybe a million times per second, which is sufficent for the trigger system to identify and record data from each one individually.
There are layers of data filters which can sort these events into different categories, depending on what's observed. It is possible, and is a significant part of most analyses, to reconstruct all of the momentum and energy seen in the detector, do the vector sums, and work out both if there is missing energy and what direction it points.
Of course, that missing energy may not be due to a single particle, but can just be the vector sum of, for example, several high-energy neutrinos.
Denier,
Not sure what you mean by "sterile." Do you mean what happens if it produces particles that don't interact with the detectors (or at least, not as expected)? In that case, yes it would be difficult to understand exactly what happened, though the experimenters could still detect that something unexpected happened (via finding missing energy etc. as Michael points out). This would be an interesting and useful result; Pauli's proposal of the neutrino basically came about this way. Many experimenters before him had observed that beta decay showed a smooth energy distribution (which was not predicted), with all detected electrons having energies well below what should have had (also not predicted). Early on, a lot of scientists just figured the electrons were losing an unexpectedly large amount of energy before they hit the detectors, but Pauli pointed out that both of these phenomena could be explained if some additional particle that didn't interact with the detectors was carrying away the excess energy. Using what they knew about what was missing from the spectra, he figured out the required spin and charge of the neutrino, and that the mass would have to be very small. Which lead the way to other experiments that showed him to be correct.
So if these LHC reactions were to produce 'sterile' particles that didn't interact with the detectors, I think particle physicists would be very happy with that result. Challenged, yes, but happy.
@Michael Kelsey #3
Thanks. I did not realize the data gathering ability could work that quickly. Truly amazing machines.
@eric #4
What I mean by "sterile" is 'does not interact via the electromagnetic, strong nuclear, or weak nuclear force' A.K.A. 'Dark Matter'. Specifically I was asking about the production of the seesaw-heavy, right-handed sterile neutrino, and if we had the ability to detect such a particle.
From what I gather we do have the ability to see gaps, but because we only see the gap we don't know if it is a single low visibility particle or multiple low visibility particles. However if a gap the size of a heavy neutrino happened it probably wouldn't be missed, so we're probably not producing Dark Matter at the LHC.
“When we announced the discovery of the Higgs boson some 4-5 years ago, we had reached a significance threshold of 5σ, which has “fluke” odds of less than one-in-a-million. That threshold has been the gold standard for discovery ever since the 1970s…”
What is the sigma up to for the existence of dark matter and dark energy?
There was no particular need for you to make a show of demonstrating that you don't understand the basic concept.
^ Although if you insist, here is 4.4 σ for the late-time integrated Sachs–Wolfe effect.
After thinking about it, we can't tell if the gap is due to a phantom lightweight particle moving really fast or a phantom heavy particle moving slower. Can we?
Especially if there is a seesaw mechanism so that right handed neutrinos have a mass ratio to left handed ones, we don't know what was produced. We could have been making Dark Matter at LHC and not known it even if we can see mass going in versus mass coming out. Right?
Combined fit from Planck, weak lensing, BAO, etc.
Baryon density (Ωb): 0.0486±0.0010
Dark matter density (Ωc): 0.2589±0.0057
Dark energy density (ΩΛ): 0.6911±0.0062
The total reaction - including the missing stuff - must obey conservation laws, including conservation of momentum. So you should be able to figure out how much of the missing stuff would be rest mass vs. kinetic energy, based on the particles you do detect. But as Michael said earlier, you wouldn't be able to tell if the missing component was one particle or many; you just know what the total has to be.
@eric #12
Doesn't E=mc^2 make one exchangeable for the other?
Yes, but the system overall still has to obey conservation of momentum, which puts constraints on the mass and kinetic energy of the 'missing' stuff. If you convert mass to energy (exoergic reaction; your word for the day), the product particles must have a higher kinetic energy to make up for it.
I guess its fair to say that the solution space for the missing stuff could contain a range of solutions. If that was your point, its correct. The point I was trying to emphasize is that it isn't 'anything goes.' The possible solutions for what the missing stuff could be will be constrained. When you factor in other conservation laws, the solutions are often highly constrained.
To eric #12:
“The total reaction – including the missing stuff – must obey conservation laws…”
MUST OBEY conservation laws?
Do the conservation laws that must be obeyed include the conservation of energy?
If so, and if dark energy is the cause for the alleged *accelerating* expansion of the universe, how is dark energy conserved?
It seems to me that DE would be *increasing* in its causing not just continual expansion but continual accelerating expansion.
Endless S.N. reruns are just sad.
^ More direct answer: You've already been told that energy isn't conserved in general relativity.
@ Denier,
It's all explained over here:
https://profmattstrassler.com/articles-and-posts/relativity-space-astro…
Splashing water ;)
To everyone who is trying to respond to S.N.
Don't bother. He is very obviously a troll and feeding him will not solve anything. Just leave his posts unanswered.
@Elle H.C. #18
Thanks for the link. The picture is much more clear now.
As I've pointed out before, I'm immune from "feeding" him, as I've been "added" to his brain-dead "No Fly/Do Not Call list" from RI.
Observe its habits more closely. The cravenness is a feature, not a bug.
Hey Ethan,
Here’s a subject for a potential future article of yours –
The Principle:
http://www.breitbart.com/radio/2016/08/10/filmmaker-rick-delano-the-pri…
There's nothing like ignoring replies to one's preceding comment in favor of barfing up some movie plug from Breitbump that says thought.
"Doesn’t E=mc^2 make one exchangeable for the other?"
But momentum isn't conserved if you just parcel out the energy. You have to conserve BOTH at the same time.
If conservation of energy were all that was required, a Newton's Cradle would operate much differently: throwing two balls could cause ONE ball to swing from the other end at twice the speed (2mv=m2v), or two balls at different velocities, or three balls, or bouncing of the original pair and a different speed of the remainders.