This post comes about as an attempt to write down, slowly and carefully, a simple version of the "idealised GHE model". This apparently simple concept causes lots of confusion, though mostly amongst people who want to believe there are fatal flaws at the heart of climate science.
Before I go on: this is an idealised model. No-one actually does any real calculations from it. Some of the concepts involved are used in GCMs, but anyone who says, for example, "aha! You've averaged the diurnal cycle in your model, therefore the GCMs are wrong" isn't thinking.
Lets consider a very heavily idealised model of the greenhouse effect. There's only one "atmospheric level", and energy transport is by radiation only. Very importantly, this is an equilibrium model. In each layer (sfc, atmosphere, space) the fluxes balance; none of the layer's temperatures are changing over time.
[SUN. SW to Earth] ^ [LW to space] (1)
[S=1362 W/m2; 0.7*S/4=238 W/m2] |
V ^
------------ V ---[ATMOSPHERE Ta]-----+------------- (2)
V ^ V
V | |
V ^ V
V | |
V ^ V [LW absorbed at sfc]
/////////////////////[SURFACE Ts]//////////////////// (3)
The surface, at temperature Ts, emits thermal radiation given by (rho)Ts^4. The atmosphere at temperature Ta emits thermal radiation (upwards and downwards, this is important) according to the Stefan-Boltzmann law given by (rho)Ta^4; (rho) is the Stefan-Boltzmann_constant, 5.67/10^8 W/m^2/K^4. Or close enough for our purpose here.
[Update; note, although I've written (rho) here, and it all works of course because it is just an identifier, the usual symbol is the Greek "sigma", so (sigma) would have been clearer. Thanks to mz.]
You'll see at once that this is not a strictly realistic model of the Sun-Earth-Atmosphere-Space system. Never mind, we'll not worry about that much now. Lets just note the salient features of the model, without justifying them:
1. The Earth is assumed to be uniform and a perfect blackbody. Its also either perfectly super conducting, or some other appropriate set of assumptions to get a uniform surface temperature. It still spherical, though, if that helps.
2. Solar radiation, S, is 1361 W/m2. But because the Earth is a sphere, and the ratio of the area of a sphere (4.pi.r^2, Earth's surface area, which emits thermal radiation) to a circle (pi.r^2, Earth's cross-section to Solar radiation, which determines how much Solar we absorb) is 4, the average insolation per unit area of the Earth is 1361/4 at the top of the atmosphere. But since Earth's albedo is ~0.3, the average insolation at the surface is 0.7*1361/4 = 238 W/m2 (if you do the approximations slightly differently you get 239; no-one cares about that difference at this level of accuracy).
3. In this version, the atmosphere is entirely transparent to Solar radiation (also known as SW, for Short Wave) and entirely opaque to Earth's emitted thermal radiation (also known as LW, for Long Wave). And for the purposes of the model, SW and LW occupy non-overlapping bands; this last assumption is realistic, unless you're being really picky.
4. Energy transport is by radiation only. This is not at all realistic for the totality of the Sfc-Atmos system, but it isn't too implausible if you think of the model "surface" as representing some level of the atmosphere, perhaps 400 hPa.
5. There is only one "atmospheric" level, and only by convention is it called "atmosphere": it could be a sheet of glass. It has no defined height above the surface.
We can now write down the energy balance of the three layers:
(1) Space. Solar radiation (0.7*1361/4 = 238 W/m2) absorbed by the Earth equals the LW radiation lost by the Earth. Hence,
238 = (rho)Ta^4
Woo, that's good. We can immeadiately work out the temperature of this layer:
Ta = fourth_root(238*10^8/5.67) = 254 Kelvin.
(2) The Atmosphere. This one is a bit harder, but not much. The Solar SW radiation doesn't appear, since the atmosphere is transparent to SW. So the terms are: the upwelling LW radiation from the Earth's surface; balanced by two terms, from the upward (lost to space) and downward (absorbed by the Earth's surface) thermal radiation emitted by the atmosphere. The crucial point here is that there are these two LW "loss" terms, and they must be equal, because they are both thermal emission from each side of an object, the atmosphere, with the same temperature, Ta. So:
(rho)Ts^4 = 2 * (rho)Ta^4.
From which the (rho) cancels, leaving:
Ts = fourth_root(2) * Ta.
Which is nice and simple. We now know the surface temperature, and its warmer than the atmosphere, by a factor of fourth_root(2) = 1.19. Ts = 302 Kelvin; roughly.
(3) The surface. Note that we've now run out of variables to find the value of, since we know the sfc and atmospheric temperatures, so we'd better hope the sfc budget balances. The terms are: incoming solar, 238. Outgoing thermal, (rho)Ts^4. And incoming atmospheric thermal, (rho)Ta^4. So:
238 + (rho)Ta^4 = (rho)Ts^4.
Happily, if you look back to the balance for layer (1), you'll see we've already deduced that (rho)Ta^4 = 238, so this equation just says:
2 * (rho)Ta^4 = (rho)Ts^4
Which makes it a duplicate of the balance for layer (2), and thus it must balance, because we've already balanced that layer. So it all ends happily, phew (you may be tempted to see that as sleight of hand but it isn't; it had to happen like that, or the physics would have been wrong).
In summary
We end up with an energy balance that looks like this:
[SUN] ^ [LW to space] (1)
[S=1362 W/m2; 0.7*S/4=238 W/m2] | [= 238 W/m2]
V ^
------------ V --[ATMOSPHERE 254 K]---+------------- (2)
V ^ V
V | |
V ^ V
V | |
V (rho)302^4 ^ =238*2 V [LW absorbed at sfc=238 W/m2]
/////////////////////[SURFACE 302 K]//////////////// (3)
Having done that...
You've probably guessed that I've written all this down because someone else has got it wrong. That someone is "Derek CAVEMAN SCIENTIST", and his version is a set of slides at www.globalwarmingskeptics.info/thread-2250.html (Update: actually he's changed them. Sigh. Fortunately I took a webcite. As far as I can see from a quick scan he has removed some redundant pics, but his basic errors remain).
He starts off with some pics he's found. Lets go through them.
A picture roughly corresponding to the above occurs in a Beeb page the greenhouse effect which appears to be part of some "GCSE bitesize" thingy. They don't put any numbers on the arrows (I suppose S-B is beyond GCSE), (?hence?) they don't explain the /4 geometry, and they do make it easy to mistake the thermal LW emitted by the Earth for "reflected heat" (though if you bother read their text they do get it right). They also don't explain energy balance, or that the downwelling LW is part of it. Overall, not a very good effort I'd say.
Analogies with a real greenhouse are unhelpful. Real greenhouses work differently. Not everyone realises that, and some people get hung up on the terminology and forget that they're trying to understand reality.
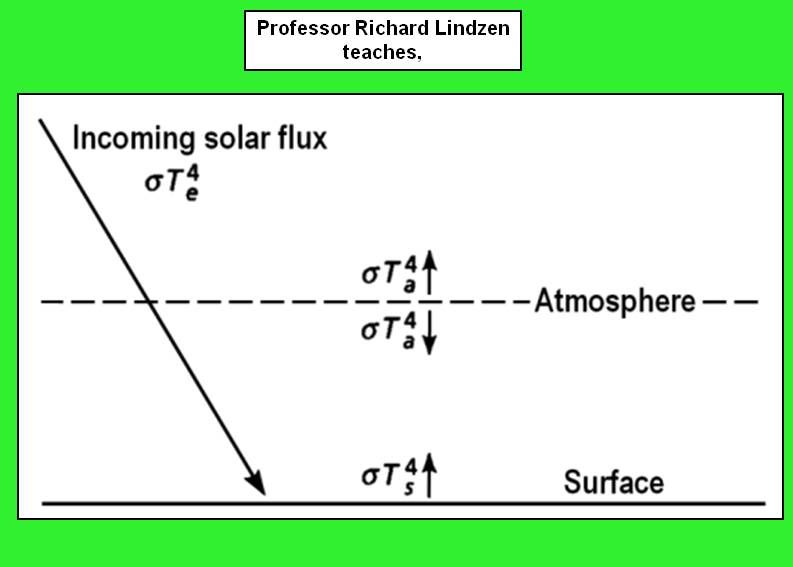Here's a pic that corresponds closely to mine. Its attributed to Lindzen, and that's quite believeable, because about basic science he's likely to be right.
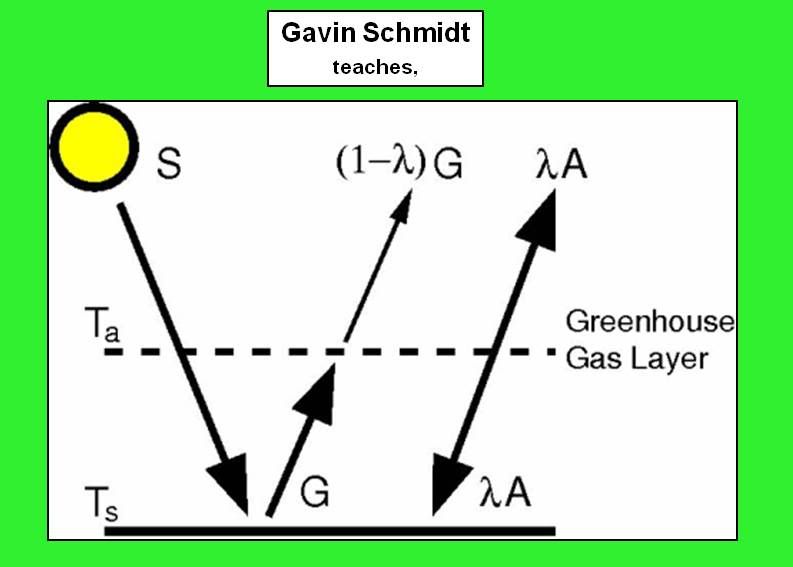This one is attributed to Gavin, and that's plausible too, because this one is also correct. It reduces to the previous one, or to mine, if you set (lambda) to one. It isn't clear to me if the source for my pix realises this. (lambda) represents the absoption of LW in the "atmosphere" layer. If (lambda)=1 all the LW is absorbed, as in my model; if (lambda)=0 the atmosphere is transparent to LW, and there is no greenhouse effect. This complexity adds nothing fundamentally interesting. Also the real atmosphere is opaque to LW when its of any thickness, so (lambda)=1 is reasonable at this level of detail.
Or, you can call the incoming solar Is*(1-(alpha)) where (alpha) is the planetary albedo of ~0.3; 1-0.3 is the 0.7 I'm using explicitly. This makes no difference; its just a matter of labels. You can also fold in a surface albedo, too; again, it makes no real difference.
But, what you can't do is this: which is to say, write the wrong numbers onto the arrows. This is obviously broken, because the surface energy budget doesn't balance, and nor does the atmospheric layer balance either. Not at all by coincidence, they are out of balance by the same amount, 239. This pic is described as "a fair and accurate representation of all the above model 2 diagrams".
What's gone wrong? Well, as we saw from my correct version, the upwelling LW from the surface needs to be twice the downwelling (and upwelling) from the atmosphere, in order to make this model balance. And that happens because the surface is warmer than the atmosphere. In the picture I've inlined, the author has the surface emitting 239 W/m2, which will only happen if Ts = Ta. So, this picture can be sort-of considered as an unstable state, before it equilibriates, if you want to be generous. You can make the picture correct by replacing the erroneous "239" pointing to box 3 with the correct value, 2*239.
[Update: thinking about this, is it possible to explain the Author's confusion by him thinking this is a diagram of energy flowing round the system, in a step-by-step way? That is to say, he thinks the leftmost arrow happens *first*: SW enters and strikes the Sfc. *Then* he thinks the sfc emits LW, and naturally (on this incorrect view) he thinks that must be 239 too. *Then* he thinks the atmosphere emits thermal radiation. I think that really is what he's doing wrong. Oh dear. That isn't at all how the diagram should be interpreted: everything happens at once, and everything is in equilibrium. There is no step-by-step to it. The numbers on the arrows (1 to 4) do not represent a sequence in time. Uupdate: this is indeed how he is thinking; I notice that he actually explicitly says "One is supposed to follow the diagram from left to right. ie, arrow 1, arrow 2, arrow 3 and then arrow 4." Oh dear.]
What would happen, physically, in a world that really had those arrows on it? Well, instantaneously, to make the sfc upwelling LW consistent with the surface thermal radiation, Ts would have to be 254; ditto for Ta. From that picture, the surface would start to warm, because there's a positive imbalance of 239 W/m2. The atmosphere would instantaneously start to cool (before warming back to 254 later as the surface warms), because it would have a negative balance of 239. The exact path that Ts and Ta take would depend on the heat capacities of the layers, but eventually it would equilibriate at my values.
Returning to the slideshow, our Author has got badly confused, because we next come across:
Ta has already been described by him as sunlight in (240W/m2) = Tg (240W/m2) = Ta (240W/m2)
This makes no sense at all: the incoming 240 W/m2 (or 238, or 239, whatever) is, errm, in W/m2. It can't equal Tg (T_ground; my Ts) to Ta, because Tg and Ta are in Kelvin.
Our author then presents this pciture as "Professor Nathan Phillips also explains in this pdf Greenhouse effect "theory" model 3." I don't know why he calls this "model 3"; its the same as the previous ones.
The Greenhouse effect “theory” as clearly depicted in the above diagrams has (at least) four fatal flaws, which are as follows.
This is the bold assertion our author makes. Lets go through it:
1) A 2 parallel plane (2PP) model used - Inappropriate, does not apply to earth.
This an idealised model, so its not expected to be entirely accurate. But this criticism isn't a very good one: on Earth, the vertical scale is small compared to the horizontal, so representing the atmosphere as a plane is quite reasonable.
2) The power of sunlight received at the top of earth’s atmosphere is divided by four (P/4) - This is unphysical, and can not be applied to earth.
This is a failure of abstraction. I think our author understand the area-of-circle divided by area-of-sphere bit; what he hasn't realised is that if you're applying a time-independent view you can average over the day-night cycle, and over the Earth's geographical area.
3) In the model 2 type, 240W/m2 is absorbed by earth’s atmosphere which becomes 480W/m2 radiated by the atmosphere. The atmosphere is depicted as emitting the same power or amount of energy both up and down, ie, twice what it receives. 240 W/m2 of energy is created. - Energy can not be created.
All we're seeing here is the Author's confusion. He has written the wrong numbers onto his "model type 2" diagram, and then complained that the numbers are wrong. Um.
3 cont) In the model 3 type the atmosphere is depicted as radiating 240W/m2 before the surface warms it. This is double accounting, at best, and is by any other name, creating energy.
No, the picture is time-independent. Its a steady state once all layers have come to equilibrium. The surface has, indeed "warmed the atmosphere" and the atmosphere has "warmed the surface". There is no double accounting, all fluxes balance, no energy is created or destroyed.
4) In the model 2 type earth's surface receives 480W/m2, but is depicted as only radiating 240W/m2.
Only in our Author's broken version. See above.
We now come on to a pile of pix of what our Author calls "model type 4". these are no longer the idealised model; instead, they're considerably more complicated diagrams dealing with a whole pile of extra processes that we deliberately abstracted out of the simple model to make it tractable. If you don't understand the simple model, you're unlikely to get far with this one.
That's about the end of the slide show.
Returning to the divide-by-4 bit, which seems to worry people
As I said earlier
Solar radiation, S, is 1361 W/m2. But because the Earth is a sphere, and the ratio of the area of a sphere (4.pi.r^2, Earth's surface area, which emits thermal radiation) to a circle (pi.r^2, Earth's cross-section to Solar radiation, which determines how much Solar we absorb) is 4, the average insolation per unit area of the Earth is 1361/4 at the top of the atmosphere.
This seems to worry some people as "unphysical". Weeell, if it helps you, rest assured that GCMs don't do this: they apply the diurnal cycle or radiation point-by-point, adjusting for latitude, and they include the effects of clouds and atmospheric scattering and surface albedo.
Another way of looking at it is, how could you rescue it so it was physical? One way is to render the Earth entirely uniform, and super-conducting to heat. In which case the "dark side" gets its share, irrespective of whether the sun is up or not. You have to make the "atmosphere" super-conducting too, of course.
But a better way is to realise that its an approximation: we know that in the real world, there is a day-night temperature cycle but (at least, say, over the oceans - we can imagine all this going on in an aqua-planet world if we like) its not very large. And then you'd need to fold in the latitudinal dependence too.
This all returns to my The New Aristotelians post: in order to make progress in science, you need to understand what to abstract, and what to keep.
Another way of thinking about it...
...which is in fact exactly the same way of thinking about it, even further simplified.
If you don't like the numbers of the maths, don't despair, there is hope for you. Its possible to get a qualitative understanding with no numbers at all.
* Agree that the Earth is heated by the sun,
* and that it emits thermal radiation to balance the heat from the sun.
* In the absence of atmosphere, that's it.
* With an atmosphere (that absorbs some or all LW, but no SW) the LW from the Earth warms up the atmosphere,
* which emits thermal radiation upwards and downwards.
* Therefore, the Earth is warmer in the presence of an atmosphere, because it is heated by two sources: the sun and the atmosphere.
Easy, no?
Very late update
From March 10th: reading some comments at ATTP I think I begin to understand where the "its all the lapse rate" Doug-Cotton-types are going wrong (other than their a-priori insistence that it can't possibly be GHG's): they have in mind the black-body T, correct, and the lapse rate, correct, both of which they at least half understand; and the "effective emission height", which they don't understand at all. But they think of it as fixed. So they think of the sfc temperature as being from the temperature profile (as set by EEH and lapse rate) at the sfc. Or something like that - it can be hard to tell whether they think they're starting from the EEH or the sfc. But all this is so obviously wrong (the EEH isn't fixed) that its hard to know what else to say.
Refs
Every man and his dog has their own pet explanation of the greenhouse effect. If you're not a "skeptic", and you can cope fairly easily with the maths and with S-B, then you probably want a more advanced version. Like the wiki one, or I'll collect some here.
* Learning from a simple model - Gavin's, at RC. Goes through the maths faster, and therefore gets beyond my very simple model to more interesting stuff.
The pic is Klee; found via the lost.
* Science of Doom Reference post - goes through some of the basics.
- Log in to post comments
My 'slide' is from here: http://www.realclimate.org/index.php/archives/2007/04/learning-from-a-s…
You really should use QuickLatex for the equations though.
[Ta. I'll link that from a newly created references section. Eqs: hmm, yeah -W]
w00t -- ASCII art!!1!!
But seriously, your "Another way of thinking about it..." explanation is exactly the view of the greenhouse effect that I've been trying to encourage: "The Earth is warmer in the presence of an atmosphere, because it is heated by two sources: the sun and the atmosphere." None of this "like a blanket" or "absorbs and re-emits" or other silliness.
I may have missed it, but it seems that you're ignoring the emissivity in your simple model. Was that intentional, or am I missing some subtlety?
[I didn't quite ignore it; I said "the atmosphere is entirely transparent to Solar radiation... and entirely opaque to Earth’s emitted thermal radiation". Its easy enough to fold the emissivity into the model if you want to, but it complicates the maths a little and it doesn't add anything fundamental to the solution. Gavin's post adds this -W]
Okay, I read Gavin's post after I posted that comment. You've essentially just assumed lambda = 1, and it should be something like 0.8 (at least, I think that's what you've done).
I've learned quite a lot from your and Gavin's post. My idealised GHE was even simpler than what you're presented here :-)
[I don't quite understand Gavin's post, because the "true" emissivity has to depend on the thickness of the atmosphere, which in this model is somewhat arbitrary. And in the real atmosphere is effectively opaque, at least at certain wavelengths. Thinking about it, Gavin's number probably wraps up both the thickness and the spectral windows stuff; and of course in this version of the model there are no "windows" because apart from LW/SW we aren't considering wavelength dependence -W]
I also found Gavin's post a little confusing. I think I've also seen the emissivity presented differently. Elsewhere I've seen the net outgoing flux (wavelength averaged) as eps sigma T_surf^4 with eps being called the emissivity and usually eps = 0.6. If I look at Gavin's post, the net outgoing flux is
out Flux = (1 - lambda)G + lambda A
lambda A = lambda G/2
so, you can rewrite this as
out Flux = (1 - lambda) G + lambda G/2 = (1 - lambda/2) G
which ends up being the same as I've seen before.
I must say, though, that the nice thing about the way you've presented it is that one can essentially assume that it's opaque to the outgoing surface flux and you get a pretty good representation of the process.
I'm assuming that I can guess where you discovered a link to this erroneous description of the GHE.
[You can also care about the surface emissivity, and if you do you need to make sure whether you're talking about sfc or atmospheric. Again, for this model, the surface emissivity doesn't matter much - all that happens if (sfc emissivity is less than one) is the sfc gets hotter for a given level if incoming radiation, because the thermal radiation is reduced. In the real world a hotter sfc has consequences - for evaporation, for example - but for this model it has no consequences other than changing the value of the thing called Ts -W]
Thanks for the article, William. Out of interest, roughly how many of the incoming 238 W/m^2 are turned into kinetic energy, such as winds and the hydrological cycle?
[My pulled-out-of-thin-air answer is that the atmosphere, considered as a heat engine, is very inefficient; I'd guess perhaps 1%. Others will know better.
Update: http://www.lpl.arizona.edu/~rlorenz/clouddiss.pdf suggests I was about right. And the bit about raindrops is interesting -W]
Of course, Eli had even a two level model in his GT discussions/paper
and an interesting (to Eli) take on what happens near the surface. If you really look in detail, the downward radiation to the surface is probably not as important as downward transport of thermal energy from the adsorbed radiation by eddy diffusion.
Interesting confusion in #6. ALL of the energy absorbed in the atmosphere is turned into kinetic energy by collision, most of it in the form of heat, a bit in the form of work. Much of the kinetic energy is re-radiated as IR. Much of the adsorbed solar energy in the troposphere goes to evaporation of water droplets. Much of the adsorbed solar energy in the stratosphere goes first to dissociation of ozone.
Eli #6: I didn't write my question correctly. If Earth (by which I mean the planet and its atmosphere) is receiving 238 W/m^2 of electromagnetic radiation (mainly light photons) and it is radiating 238 W/m^2 of infrared photons there is zero net energy to perform mechanical work (to power the winds, currents, etc).
Earth isn't a 100% efficient perpetual motion machine (such things don't exist) therefore it must be radiating less power into space than it is absorbing from the Sun. I'm just curious to know the size of the difference.
[I think your original question was better :-) All the energy received gets re-emitted to space, because no energy gets "stored" in winds. But some of the energy is transiently in kinetic energy. And if you read the paper I ref'd, the answer does turn out to be about 1% -W]
Pete, I think there is still some confusion. Energy is conserved.
You seem to be implying that when we do work, we use up some energy. This isn't actually correct. When we do work, we typically convert one form of energy into heat.
Consider the following. I push a box along a surface with a force that accelerates the box to some final speed. In doing this, I've converted chemical energy (food) into kinetic energy. However, if the surface has friction, then the box slows down and stop. All my initial energy has now been converted into heat.
The same happens in our climate. We receive energy from the Sun. This energy can be used to do work. But all the kinetic motion gets dissipated (if it didn't, winds might get forever faster) and is turned into heat. On average, then, an equal amount of energy is radiated back into space as we receive from the Sun. If this didn't happen, we would just continue to warm (i.e, the heat would build up). That we typically don't (although we kind of are at the moment) means that we lose as much energy as we gain.
Given that Eli is also a physicist, he can probably correct anything I've got wrong (hopefully not too much :-) )
Thanks for the paper, William. (I hadn't spotted your update to #6 until you mentioned it in #9). My original question was much better :-)
For most subjects I can usually find scientific (i.e. correct) answers to my questions via web searches, but on this subject I encountered many articles and papers that I'm fairly certain were not based on the science of this universe.
Oh yeah, the Earth also rotates.
@ #10
Thanks for your very clear explanation. I was thinking through it while cooking dinner when my error suddenly became obvious. The net heat power is zero, but the Sun's energy is travelling *through* Earth's systems on its way into space, which takes time. Therefore, Earth can convert it into as many different forms of energy as it likes before finally converting it all back into heat and radiating it into space. It's equivalent to having a zero interest loan.
For each second of heat transfer delay there are 238 joules/m^2 available to drive Earth's systems. As you pointed out, the joules that are turned into kinetic energy will eventually turn back into the same number of joules of heat then radiate into space.
Since the albedo of the solid and cloud surfaces is some two to eight times larger than the albedo of the water covering most of the planet, some dynamics are to be expected.
Russell, Eli expects you mean in the visible and NIR?
Pete Atkins, here is a good cartoon:
http://www.atmosp.physics.utoronto.ca/people/guido/images/climate_syste…
Models that are based on the completely false physics that radiation from a colder atmosphere can actually help the Sun in raising the temperature of Earth’s surface are a complete fiction. It cannot do so. Physicists will tell you (if you even bother to ask a specialist in thermodynamics like myself) that such radiation undergoes what they call “pseudo scattering” in which it is immediately re-emitted in a resonating process, without any of its electro-magnetic energy being converted to thermal energy. This provides some of the electro-magnetic energy in the SB calculation for the warmer surface, and thus slows radiative cooling, but it can have no effect on molecules colliding at the interface and transferring thermal energy by conduction and evaporative cooling.
But none of this is what really determines planetary surface temperatures anyway. The base of the Uranus nominal troposphere is hotter than Earth, and yet it receives no direct solar radiation worth mentioning.
Valid physics can be used to confirm beyond a shadow of a doubt that a gravitationally-induced temperature gradient will always evolve spontaneously in a vertical plane in any solid, liquid or gas that is exposed to a gravitational field. This happens at the molecular level where molecules swap kinetic energy and gravitational potential energy when in free flight between collisions. No one has correctly rebutted this, and wires outside cylinders also develop thermal gradients so no perpetual motion can occur.
There is a predetermined thermal profile in Earth’s atmosphere caused by gravity which, without water vapour or greenhouse gases, would intersect the surface in the vicinity of 25C, but then water vapour reduces the gradient (due to inter-molecular radiation, not the release of latent heat) and we end up with a mean of about 15C.
It is natural cycles, probably regulated by planetary orbits, which are the primary determinants of climate. That’s why it’s not carbon dioxide after all.
[Yawn. You've written a pile of words, with no meaning. You're not a physicist, you're an English grad. Try engaging with the maths - don't worry, its not too hard, just a few equations. Its all set out in patient detail in my post. Do, please, point out the errors in either the equations or the assumptions -W]
"I don't believe anybody who doesn't know LaTex" - science
Dear Mr.
[Dr. Consult my thesis for the LaTeX -W]
Connolley, in physics we physicians
[Are you claiming to be a physician, or a physicist? -W]
know a shit about climate. But it is nice to see that a informatician already solved all the emerging problems that need to be solved. Thank you so much.
[You're somewhat incoherent. I think you're trying to say that I've solved some problems; of course I haven't; none of this is new -W]
Dear Visiting Physicist,
You don't know a few things. First of all the radiative lifetime of CO2 in the (0,1,0) bending mode is about 1.1 sec. Second, the mean time between collisions at 1 atm is about 0.1 ns, Excited CO2 molecules change rotational states in 1 to two collisions. Further the vibrational deactivation time is about 1 10 microsecond. That means that only about 1 in 1,000,000 excited CO2 molecules radiates directly. Mostly the vibrational energy is quickly degraded to kinetic energy (e.g. thermal excitation).
Always a pleasure to educate visiting physicists:)
@ Eli
"Dear Visiting Physicist, You don’t know a few things"
Heh. Congratulations, Eli, on the climate blog understatement of the year.
OK The errors in the assumptions relate to how radiation actual transfers thermal energy - when it does and when it doesn't. If radiation from a colder atmosphere strikes a calm water surface, can it penetrate, say, 2mm below the surface? If it can, would its electromagnetic energy be converted to thermal energy? If not, what happens to that energy? If so, we have an independent one-way transfer of thermal energy from cold to hot, decreasing entropy, which is impossible. But if you think it possible, then suppose the warmer layer of water rises to the surface and evaporates 3 seconds later. Does the energy "remember" that it can't really make its way back to the atmosphere as latent heat or by conduction and convection? Does it remember that it has to produce a "net" compensating radiative flux? The way in which climatologists bend physics is absurd and is a travesty of physics - which I have studied and taught over five decades.
Physicists are now starting to publish papers which explain how the radiation is actually "pseudo scattered" by the surface and can never penetrate the water, quite unlike the solar radiation.
You people have a lot of modern physics to catch up on, because it is now possible to prove beyond doubt that gravity forms and maintains a temperature gradient in all solids, liquids and gases, and this fact can be used to explain how the required energy gets into the surface of Venus to raise its temperature slowly over the course of its 4-month-long day. It can also explain why the core of our Moon is far hotter than the surface ever is, and why the temperature gradient in Earth's outer crust is more than 20 times steeper than that in the hot mantle.
Yes, you have a lot to learn. I doubt that you can explain why the base of the Uranus nominal troposphere is hotter than Earth's surface, even though no internally generated energy or direct solar radiation reaches it.
If anyone here can answer these questions my respect for your knowledge of physics will be somewhat elevated.
[Still a notable lack of maths and instead rather a lot of words. That, coupled to a deliberately-vague reference to unspecified papers, doesn't exactly fill me with confidence. Your "questions" relate to radiation penetrating water, and so are completely irreleveant to the model we're talking about, which works fine for a solid surface. Did you realise that? But, I'll try answering anyway:
1. If radiation from a colder atmosphere strikes a calm water surface, can it penetrate, say, 2mm below the surface? [The "colder" bit is irrelevant. The exact penetration depth is also largely irrelevant; LW is absorbed in the top few millimeters (Descriptive Physical Oceanography: An Introduction; Lynne D. Talle et al.]
2. If it can, would its electromagnetic energy be converted to thermal energy? [Yes, the LW gets converted to thermal]
3. If not, what happens to that energy? [Irrelevant, because of the answer to 2]
4. Does the energy "remember"... [No.]
Um, so, I've answered your questions but it doesn't seem to have been very illuminating. Did that help you? -W]
Primary, yes. Only? No. Currently dominating? Oh, if only there were some way to know what planetary orbits were doing at any given time! I guess we'll never know...
"The surface, at temperature Ts, emits thermal radiation given by (rho)Ts^4. The atmosphere at temperature Ta emits thermal radiation (upwards and downwards, this is important) according to the Stefan-Boltzmann law given by (rho)Ta^4; (rho) is the Stefan-Boltzmann_constant, 5.67/10^8 W/m^2/K^4."
By rho, do you mean sigma? I've never seen Stefan-Boltzmann denoted by rho, neither in http://en.wikipedia.org/wiki/Stefan%E2%80%93Boltzmann_law
[Um, quite likely. My Greek lettering was never up with the best :-( -W]
What is emitted from the surface is radiation carrying electro-magnetic energy. Not all of that electro-magnetic energy has been generated by thermal (kinetic) energy that was in the surface: much of it is merely re-emitting the electro-magnetic energy that was in the back radiation. That energy never was converted to thermal energy. This is what you don't understand.
[I don't think that's true. The absorbed LW becomes kinetic/heat, which then gets re-emitted as thermal radiation. If you're suggesting that any significant fraction of the downwelling LW is re-emitted by the individual sfc molecule that absorbed it, then I think you're wrong. But we can try to find out: do you have a reference for your claim? -W]
When low frequency radiation (with low energy photons) is emitted in a microwave oven it does not raise the temperature of a plastic microwave bowl, but the Sun's radiation would do so.
[Because the plastic bowl doesn't strongly absorb at microwave wavelengths. It does strongly absorb in the viz -W]
Yes it does happen to raise the temperature of water molecules in food, but it does so by physically rotating those molecules in synchronisation with each wave, so that is not normal absorption, and slightly higher frequencies may have no effect if they don't resonate.
[I think you're totally lost. Where are you getting all this stuff from? -W]
@ #17
"that such radiation undergoes what they call “pseudo scattering” in which it is immediately re-emitted in a resonating process, without any of its electro-magnetic energy being converted to thermal energy"
You are claiming that materials have an absorption coefficient of zero for wavelengths longer than the equivalent wavelength of their surface temperature. If true then RF and microwaves wouldn't be able to heat anything on this planet.
Similarly, an infrared laser having a wavelength of around 10 micrometres would not be able to heat its target to much above room temperature: because a hotter target would immediately re-emit the laser radiation in a resonating process, without any of its electro-magnetic energy being converted to thermal energy. Clearly, this is absurd.
Oh goody, new pinatas. The Weasel has all the luck.
[There's an old Go proverb: the stronger player always seems to have all the luck -W]
As to" It is natural cycles, probably regulated by planetary orbits, which are the primary determinants of climate."
Only the Earth's planetary orb, not Jupiter or whatever else. We appear to be deeply into Landscheidt and Gerlach territory with this bunch
Yeah that's what Joe Btfspik would say
FWIW microwave radiation is strongly absorbed by molecules with dipole moments (basically an asymmetric distribution of charge). Water has a humongous dipole moment and absorbs strongly. Most plastics have very small dipole moments and absorb hardly at all.
Eli thinks he will apologize to Gerlich, Tscheuner and Kramm for thinking that they were thegreatest possible box of rocks. Maybe not.
Eli needs him some brackets
If radiation from a colder atmosphere strikes a calm water surface, can it penetrate, say, 2mm below the surface?
{no}
If it can, would its electromagnetic energy be converted to thermal energy?
{It's converted to thermal energy at the surface or near it}
If not, what happens to that energy?
{See previous answer. Conduction is an important heat transfer mechanism in a liquid}
If so, we have an independent one-way transfer of thermal energy from cold to hot, decreasing entropy, which is impossible.
{If cows were horses pigs would fly}
{Oh yes, the lapse rate was explained about 100 years ago, glad news has finally come to whatever planet you are commuting from..}
William, I'm very interested in learning a lot more about the greenhouse effect, but the questions I'd most like to ask at the moment are too humiliatingly naive to ask on a public forum :-(
A pointer to someone who could spare the time to answer my questions via e-mail would be greatly appreciated.
[It would be best to put them here, in comments. Or at least the first couple of questions, to get some idea of the kind of things you're wondering about. Then I could write an exciting blog post about it. Seriously, one of the things I learnt years ago in seminars that if you're sitting there wondering what the speaker is going on about, so are half the rest of the room, but they're afraid to look silly so you should ask. Or, you can use wmconnolley at gmail in the normal way -W]
I see. So you have described an independent isolated process in which thermal energy has been spontaneously converted to electro-magnetic energy in a cold region of the atmosphere and (as about 70% of the world's back radiation does) it strikes a water surface, but you then think it can actually penetrate that water surface by, say, 2mm and have its electromagnetic energy go through the complicated process of being converted back to thermal energy, thus raising the temperature of that layer of water. Hence in that completed, independent process (for which there is no subsequent dependent radiation process) you have transferred thermal energy from a colder region to a warmer region and thus caused entropy to decrease.
Well, I guess you had better change the rules of the game and edit the Wikipedia entry for The Second Law of Thermodynamics next.
I notice it was edited recently, removing the paragraph which correctly explained that, in a gravitational field, the state of thermodynamic equilibrium which evolves spontaneously is one which must exhibit a thermal gradient. That paragraph could have been used to explain, for example, how the necessary energy gets into the surface of Venus in order to raise its temperature by 5 degrees during the Venus day from 732K to 737K, even though only 20W/m^2 of direct solar radiation reaches the surface, but over 16,000W/m^2 would be required to raise the temperature in that range with a net input of energy of course.
[Ha ha, you mean this? Like it says, removed good faith but incorrect and unsourced edit; see talk page. And indeed you can see the talk page. And if you really believe what you say, you could even go to the talk page and try to demonstrate that you do know what you're talking about. But I don't think you (or Douglas Cotton) would fare well against Chjoaygame -W]
Oh, and why is the base of the nominal Uranus troposphere hotter than Earth? These planets are not still cooling down, and Uranus has no significant internal energy generation or solar radiation in its lower troposphere - or any surface there for that matter.
[You're back, but still on words not maths. I'd like you to answer a simple question, which so far you haven't: do you agree that all the equations I've given are accurate, and that the physical system (given the simplifications described) is correct? Naturally, if you answer No, you also have to state clearly whether its the equations, the physics, or the simplifications that you believe to be in error, and if so in what way -W]
[Sorry guv. I'm going to insist on an answer to my question in #32 before any more comments from you make it through. Once you've answered, I'll restore your fine comments -W]
The deductions you make from your equations are wrong because, as I have already correctly stated, "The errors in the assumptions relate to how radiation actual transfers thermal energy."
I have enlarged upon that in subsequent comments pointing out that your answers describe a process that violates the Second Law of Thermodynamics because it postulates a decrease in entropy.
[Rest snipped, because veering off course. No, I'm afraid you haven't even attempted to show how my process violates the SL. From your failure to describe any of the equations as wrong, I can assume you agree that all the equations are correct, and the energy balances are all correct. We're left with your rather vague assertion that "The errors in the assumptions relate to how radiation actual transfers thermal energy." Its not at all clear to me what you mean by that. We're agreed, I hope, that if solar (SW) radiation strikes a solid black body then the radiation is absorbed, and re-emitted as LW as described by S-B. And the same for the LW. So I'm at a loss to understand exactly what it is you disagree with. Please state your disagreement more precisely, as befits someone claiming to be a physicist -W]
[See #33]
No the energy balances in your calculations are not correct, because you have assumed that all passages of radiation actually transfer thermal energy. They don't. I have given you an example concerning back radiation striking water
[Snipped, again, you're veering off topic and you're still not answering. You don't seem to understand that your points about water are irrelevant; in my little toy model, the surfaces are solid, not liquid. I'm afraid that "all passages of radiation actually transfer thermal energy" doesn't really mean anything, at least to me. If thermal radiation strikes a black body, it is absorbed. It must be; this is part of what "black body" means. When that radiation strikes a solid surface it must necessarily be converted into thermal energy, no? In which case, your statement is obscure -W]
I can't decipher enough of Visiting Physicist's word salad to properly respond. As far as I can tell he's off in Tim Ball / Doug Cotton territory, i.e., the greenhouse effect doesn't exist and it's all due to hydrostatic compression, or something similar. Would that be a fair summary?
[I think so. Its beginning to look very familiar. Its probably telling that the edit to wiki that he praises was made by an account called "Doug Cotton" -W]
Your calculations are wrong because they do not fit with reality. The onus is on you to find out why.
[No, not really. Mine are the std ones and are widely accepted. Your crit, like that of VP, is frustratingly inprecise. Its almost as though you can't actually find any flaws. But I think we can take one step forward: your "because they do not fit with reality" indicates clearly that you accept that the equations themselves are correct; you just don't accept or understand the idealisations involved -W]
If you applied them to moist air in the gap between double glazed window panes (which emulates the troposphere) you would deduce that moist air would keep a room warmer than would very dry air or argon. That is the opposite of what happens.
You have treated layers of the atmosphere as if they are black or gray bodies, but they do not fit the definition of such because they also gain and lose energy by convection, diffusion, condensation and maybe other non-radiative processes. Hence the S-B equations are inappllicable.
[I've already dealt with that: you're suffering from failure-of-abstraction -W]
Furthermore, the energy balances in your equations are also wrong. Radiation only ever transfers thermal energy from warmer to cooler regions.
[Aha! Excellent. A clear statement from you: some (or perhaps all) of my energy balances are wrong. Please tell me which, and how you would rewrite them to be correct. Essentially my picture has "four arrows": SW down, LW up, and LW u/d from the "atmosphere". Which of those do you think is wrong? -W]
There is no two-way transfer of thermal energy just because radiation may go both ways. Its electro-magnetic energy is not converted to thermal energy in a target which is warmer than the source, because all the frequencies merely resonate with the warmer target which can also emit the same frequencies with greater intensities. Only the Sun can raise the temperature of the surface, not back radiation from a colder atmosphere. But the Sun could not raise the Earth's surface temperature to the estimated mean temperature with direct radiation in the absence of a gravitationally-induced thermal gradient. This is blatantly obvious when the temperature of the surface of Venus is rising, and it is even more obvious at the base of the nominal Uranus troposphere where it's 320K.
[You notice what you've done here? You've just used words, like VP. You never ever use equations -W]
Alex Hamilton, please provide the science to answer #26. When you've done that I might be bothered to explain how microwave ovens actually work using science rather than the urban myths used in comment #25.
[Snipped again. I'm sorry, but its fairly clear you're only here to push your own pet theory. My usual response to that is "fine, just link to it, don't spam my comments" and in your latest you do provide a link - "Radiated Energy and the Second Law of Thermodynamics". Its also pretty clear by now that you're Doug Cotton, so why not start using your name? -W]
Sigh.
It continues to amaze me that people insist the greenhouse effect can't work, despite the fact that we directly measure the thing using real instruments. Look at most any micrometeorological study on the surface energy budget.
Is there really any point in arguing with such folk? I guess it might be informative for onlookers, but I have to wonder if it's worth the bother.
Is there any chance that AH and/or VP actually know what the 'base of the nominal troposphere' means? I.e., where's the surface on a gas giant? Given the core temperature of Uranus should we find it surprising that the temperature at the base of the nominal troposphere is 320K? No. On earth 300 km below the surface we find temperatures over 1000C. So Uranus' 50C seems pretty chilly by comparison. Might be why they also call it an ice giant.
Kevin. There is no evidence that the core of Uranus is still cooling off, because there is nowhere near the energy imbalance at TOA that would be expected if it were. It is just like Venus - cooling a little at night and warming back up by the same amount the next day.
You have not explained how the required thermal energy gets from the colder Venus atmosphere into its surface in order to raise the temperature by 5 degrees during its day. You can only explain this if you start with accepting that the gravitationally induced thermal gradient is in fact the state of maximum entropy and is thus isentropic with an inevitable thermal gradient.
PS This item says the core temperature of Uranus is 5,000K.
http://www.universetoday.com/19234/core-of-uranus/
Alex Hamilton, the calculated energy balance for Uranus is about 0.4 W/m2. That is, it emits less than it receives from the sun.
But do read what else Ray Pierrehumbert writes about that:
http://goo.gl/G51KkL
"The energy balance of Uranus is therefore E = 1.06 ± 0.08; " [1]
The above is a percentage of about 3.7 W/m^2 of incident solar radiation at Uranus TOA. [2]
So you are out by a factor of 10 Marco - energy imbalance on Uranus is a mere 0.04W/m^2
That's quite a small amount If you think the 5,000K core is still cooling then I would expect far more imbalance than that.
But it isn't and it won't cool significantly in a billion years unless the Sun cools significantly..
[1] http://www.sciencedirect.com/science/article/pii/0019103590901553
[2] http://nssdc.gsfc.nasa.gov/planetary/factsheet/uranusfact.html
[Thank you for posting under your True Name -W]
Doug "et al", did you follow the link I provided? I guess not.
William, are you sure it is Doug Cotton? Alex Hamilton is one of the PSI people, too, and the "et al" seems to suggest they are now some kind of hive...
[I'd missed the "et al.". That is a bit weird. Perhaps it should be read as "etc.", and qualifies the Bsc, suggesting the existence of further unspecified qualifications? -W]
[Looking at #48, I guess he did mean "etc". Either that, or its someone taking the piss -W]
Sorry - I should correct that reference to 1.06 ± 0.08. It is the ratio of emitted to absorbed flux for Uranus, but note that it could be less than 1.0, with more absorption. Neither does it necessarily have to reflect what is coming from the core, because it could be due to a small compression of the atmosphere.
Note this statement ...
‘The temperature of Uranus’ atmosphere is consistent with heating only by absorbed sunlight … .’ [3]
[3] Fix, J.D., Astronomy: Journey to the Cosmic Frontier, WCB/McGraw-Hill, New York, p. 286, 1999.
et al = other qualifications (though not relevant)
[No, sorry. You still have unanswered questions; see above.]
Douglas
"That paragraph could have been used to explain, for example, how the necessary energy gets into the surface of Venus in order to raise its temperature by 5 degrees during the Venus day from 732K to 737K, even though only 20W/m^2 of direct solar radiation reaches the surface, but over 16,000W/m^2 would be required to raise the temperature in that range with a net input of energy of course."
A Venus day is 116 earth days. A net increase of less than a tenth of a Watt lasting for an earth month would be required to raise the temperature of the atmosphere near Venus's surface by 5C.
So an extra 20 Watts/m^2 in and 19.9 and-a-bit Watts/m^2 out would solve your conundrum.
Rent a Clue asks:
I see. So you have described an independent isolated process in which thermal energy has been spontaneously converted to electro-magnetic energy in a cold region of the atmosphere
{well yes, see, here it is nicely worked out for you for the bending mode of CO2, and here, for example is a good discussion of Equipartition of Energy something that goes back to Gibbs and Boltzman and you evidently emptied from your mental locker when you took up Economics}
and (as about 70% of the world’s back radiation does) it strikes a water surface, but you then think it can actually penetrate that water surface by, say, 2mm and have its electromagnetic energy go through the complicated process of being converted back to thermal energy,
{since this is what Eli does for his day job, why yes. Collisional deactivation of molecules excited by photons is a pretty well studied area in the gas phase and even now in liquids and solids }
thus raising the temperature of that layer of water.
{That's what happens when you heat something, or perhaps you have a problem with how IR lamps heat stuff}
Hence in that completed, independent process (for which there is no subsequent dependent radiation process) you have transferred thermal energy from a colder region to a warmer region and thus caused entropy to decrease.
(How G&T. The intelligent photon theory again, with the little demons knowing that they should not touch anything hotter. A theory, which, of course, demonstrates world class ignorance.
It is only the NET of the energy transfer which is governed by the second law. On net more photons from the hotter body are transferred to the warmer one than from the colder to the hotter.}
There is no two-way transfer of thermal energy just because radiation may go both ways. Its electro-magnetic energy is not converted to thermal energy in a target which is warmer than the source, because all the frequencies merely resonate with the warmer target which can also emit the same frequencies with greater intensities.
{so just how do those photons from the colder source know that they should not convert to thermal energy in the warmer body? Intelligent little photons they are!!!.
There are two interesting things about this argument.
First, the photon demon would actually be a huge violation of the second law.
Second it assumes that re-radiation is immediate. It ain't.
Less interesting is the word salad in the last sentence with which an attempt is made to rescue the weak argument.,}
Eli, the remark "so just how do those photons from the colder source know that they should not convert to thermal energy in the warmer body? Intelligent little photons they are!!!" is very helpful for understanding the nature of the confusion, thanks.
[Hey, I was going to say that! In fact, the more I think about it, the better it is -W]
Interestingly, Lucia ("The Blackboard"), Roy Spencer, and WUWTs have all banned Doug Cotton (and his sockpuppets as quickly as they uncover them) because his notions are too bizarre for them (very few anti-science notions are too bizarre for Watts).
This simplified model of the atmosphere does more harm than good. It's the basis for the false notion that extra CO2 in the atmosphere increases global temperatures. There is no data to support this conclusion.
The many false assumptions and gross approximations in this model make application of proper physics impossible. For a start, as Eli #12 notes, Earth rotates. Consequently, the Earth's surfaces receive 239 W/m2 only about twice a day like a broken clock.
[No, you're wrong. Multiply wrong. 239 W/m2 is the daily average, across the entire globe. But the "actual" value varies geographically too. Some places at some times get significantly more, some less. But you're suffering from abstraction failure: until we can agree the simple model (on its own terms) there's no point moving on to more complex problems. You don't like the conculsions of the model, so you seek to complicate things to a degree that nothing can be learnt -W]
Secondly, the atmosphere is not a heat source like the sun.
[of course not. No-one is suggesting that it is. Did you not read my equations? The atmosphere is neither a sink nor a source; it is neutral, as it must be -W]
The heat content of the atmosphere results from whatever energy arrives from the sun today added to what was left over from yesterday. IR absorbing gases near the Earth's surface transfer almost all the absorbed LWIR to the bulk atmosphere by collisions (Eli #8 and #20). Subsequently, the warmed air rises. At sufficiently high altitudes, emissions will take precedence over collisions and, on average, around 239 W/m2 will go to space.
[Words, words, words. Can you not accept - does it not embarrass you - that the one clear defining characteristic of all you folk who deny this very basic model is that you're incapable of writing down equations? that you always resort to the ambiguity of words? -W]
No, I don't have equations to account for the additional complexity, but any less complication breeds misunderstanding as demonstrated in the comments above. Your model, like that of realclimate and elsewhere, completely ignores the roles of conduction, convection, evaporation, precipitation, let alone clouds and a host of other natural factors.
[Yes, it does. and this is deliberate. Just as our model for rolling ball bearings ignores friction, when we're trying to talk about inertia. You're stuck with Aristotle and his ox carts -W]
Thus the simple concept of an "idealized GHE model" doesn't just cause confusion, but IS the fatal flaw at the heart of climate science.
[Words, words, words. No maths. You, like "visiting physicist", are no physicist at all: you're an arts school grad -W]
What W is saying is: if you are not doing the maths, you are not doing physics. Even an arts school grad like myself can understand that.
Secondly, the atmosphere is not a heat source like the sun.
{No, it's a survival blanket See the comments at the link also}
At #56, Eli compares the atmosphere to a survival blanket that both cuts off convection and reflects back thermal radiation. I just read a recent post on his website that suggests vertical mixing, aka convection, predominates over radiation near the surface. Whereas only high up does the process become completely radiative.
[That is correct. The GHE isn't terribly important at the actual physical surface of the Earth; you need to go higher up. Fortunately, because (of course) you bothered to read my post before complaining, you knew that already, since its point 4. Oh, wait... -W]
The blanket effect near the surface is a combination of blocking by absorption and limited energy transport by a combination of eddy diffusion and radiation. The point of the post was to show that mass transport played an important role near the surface in the greenhouse effect. The net is to slow down energy transport by radiation from the surface.
Chic
"No, I don’t have equations to account for the additional complexity, but any less complication breeds misunderstanding as demonstrated in the comments above."
Most of the "misunderstandings" relate to inappropriately trying to add complexity to the model, or inventions of physical phenomena that can easily be disproved.
The "greenhouse effect" is *ever so slightly* counter-intuitive when presented in a certain "sceptical" way. A simple model makes it blindingly obvious what is going on.
So happy you did this calculation - I have wanted to see it done, but did not know the proper terminology to ask for it (Spherical cow was about as far as I got)
A question, and I apologize if I missed it in your post or the discussion (incipient insomnial brain death) - what would be the climate sensitivity in Celsius to a doubling of atmospheric CO2 in your model?
Thanks. :)
[Its not possible to answer that from my model. In the simple model here, the atmosphere is already 100% opaque to LW; this corresponds to some (non-physical) limit of CO2 saturation. If you wanted to look at that issue, you'd need to make the atmospheric absoption correspond roughly to current CO2, and then modify it for doubled CO2. Gavin's post attempts the former; doing the latter is possible, but probably not a good idea: this model really is too simple to try to do that -W]
[As before. You need to answer the questions -W]
Eli continues with his heat transfer from cold source to higher temperature sink boob.
Even Joel Shore (a co author of the hilarious G&T comment) admits that this was an elementary howler.
Now that Eli is a retired gentleman of leisure he should read some elementary physics books.
Nice post. Even I could work through the maths, so I think you should be congratulated. It also encouraged me to try again to comprehend Gavin Schmidt's slightly less simple model with renewed determination, and I think I got somewhere this time. It is so good that experts put this stuff on the net for free to help us lay people get a small flavour of the basic physics involved. I'll admit the comments have gone above my head (clearly I'm not as clever as some photons) but I'm thoroughly entertained by the suggestion that centuries of well-established physics can be thrown out so casually.
Eli and W: Now that we agree that energy transfer near the surface is predominantly convection with radiation negligible and the reverse being true at the top of the atmosphere, how can you be satisfied with the classic GHE model that reinforces the false notion that additional IR absorbing gases will warm rather than cool the planet? How do you know that Earth's surface would not be even warmer without IR absorbing gases?
[Because we don't believe in fairies -W]
Steve Milesworthy: What inventions of physical phenomena are you referring to? Are not conduction, convection, evaporation, and precipitation all well-understood integral processes involved in atmospheric energy transfer? The simple model blinds you to what is actually going on.
To better understand the idealized GHE model I made a spreadsheet, checked it against the three examples on the Wiki page, then read about albedo, greenhouse gas absorptions, etc. Going through this process enabled me to find answers to my question that I felt were too naive to ask in public. (William, did you receive my e-mail? I've managed to find some good explanations.)
Eli @#57 quite rightly pointed out that a survival blanket prevents loss of body heat through radiation. The blanket's infrared reflection coefficient is nearly 1. An average-sized adult has a surface area of approx. 2 square metres and a skin surface temperature of 33°C (306 kelvin), which means their radiated power is 1000 watts in the infrared region centred around 10 um. When in a room having an mean surface temperature of 20°C such a person would receive 840 watts from the room, a net loss of 160 watts (ignoring conduction, convection, and insulation from clothing). If, as some are claiming, a warmer surface cannot absorb radiation from a cooler surface/object, we would die very quickly from hypothermia at a radiative heat loss of 1000 watts.
To put this into perspective 2,100 kcal per day of dietary intake is 8,800 kJ/day, which is equivalent to an average power of 102 watts. Resting metabolic rate varies between individuals, but it's somewhere in the region of 60 to 80 watts -- nowhere near the 1000 watts we're radiating! Obviously, warmer objects do indeed absorb a great deal of thermal radiation from cooler objects :-)
Clothing just changes our bi-directional radiative heat transfer. The survival blanket has a reflection of nearly 1.0. Thick clothes aren't nearly as reflective to infrared, but they do reflect a very useful amount of heat back, therefore, less is transmitted to a cooler environment. The same happens in the reverse power transfer direction. The net power transfer reduces as the reflectivity increases. Which is why thermal insulation keeps warm things warm and it keeps cool things cool.
Another way to visualize the thermal insulation of clothing is to use equivalent temperatures, which is the method used in the idealized GHE model. A person inside a survival blanket is receiving back all their emitted radiation, which is exactly what would result from being in an environment at the same temperature as their skin: 33°C. From outside the blanket, it again reflects all the radiation therefore its equivalent temperature appears to be same as that of the environment. With no insulation, the equivalent temperatures are the same as their actual temperatures.
Apologies if that was too long-winded. It will take me a few days to generate some simple algebra.
How lawyerly unintelligent. Energy transfer from and to the surface is both eddy diffusion and radiation. Convection is heat flow in a gas from a warmer to a colder body, so except in an inversion there is no convection from the atmosphere down to the warmer surface
Energy transfer FROM the Earth to space is only radiation, unless you think the tooth fairy hauls it away with your kid's molars.
Thus, increasing GHG concentrations will warm the Earth.
Peter, Eli thinks you skipped a zero there. People radiation at ~100 W
Chic,
Start with paragraph 1 of "Visiting Physicist's" first post #17. It's so grammatically poor it is difficult to know what VP meant. If I assume that I can guess what was meant, I see that there is some invented physics that photons have knowledge of temperature - which they don't, and that they are (in an unspecified situation) emitted "immediately" after being absorbed, which is impossible.
A physicist and a specialist in thermodynamics would be very keen to simplify the scenarios, for example by specifying how radiation emitted by a gas cloud of a given make-up and temperature would interact with two or three different, warmer, surfaces.
The simple model doesn't blind people who know that there are other processed going on. The simple model helps explain *one* of the processes and is one step along the way.
WMC suggests that VP is an English grad, but the grammar is too poor for that.
Chic, did you write this elsewhere:
"Most infrared radiation absorbed by CO2 molecules will be transferred to other air molecules near the Earth surface. This cools the surface during the day and keeps it warmer during the night."
Eli, people may sometimes have a *net* radiation ~100 W . They'd have to be very small or very frozen to be emitting only 100 W :-)
Steve,
You brought up inventions of physical phenomena in response to my objection to the simple GHE model which leads to erroneous and/or premature conclusions such as CAGW. I have no insight into the mind of a photon. However, I doubt that a photon from a cold object will raise the temperature of a warmer object.
[Then you just aren't thinking; or you're completely ignorant of the relevant physics. That alone wouldn't be terribly surprising, or even shameful. what is shameful is you sticking to this error even when people point it out. However, than you for being so explicit about your error; it will provide fertile material for my next post, unless Eli gets there first -W]
Yes, I did say CO2 helps cool the Earth's surface during the day and keeps it warmer during the night. During the day, the air above the surface warms faster with more IR absorbing gases than without. The surface is cooler because heat transfer by convection is accelerated. After sunset, the surface will cool slower because of emissions from IR absorbing gas emissions. Note that I am not inventing any new phenomena and these processes cannot be explained by a model that doesn't account for daily variation in solar insolation.
Eli, in response to #67: Energy transfer at the surface involves all the known standard processes, not just radiation. This is precisely why the simple GHE model is misleading. If it was solely used to teach radiation, there would be no problem.
[You realise this directly contradicts your previous comment, don't you? Please tell me that you're capable of comparing the two and realising the inconsistency -W]
Unfortunately, many in the climate science community are using this model to propagate an as yet unsubstantiated hypothesis that increasing amounts of CO2 in the atmosphere will result in catastrophic consequences.
The issue is not convection OR radiation but convection AND radiation. Each has its place during a 24 hour day. Convection predominates as the surface warms during daylight.
Your statement "Energy transfer FROM the Earth to space is only radiation" belies the role of convection, endorses the misleading GHE model, and leaves you with your completely unsupported conclusion.
[You're about at your repetition limit, BTW. Further comments just saying the same thing will get snipped -W]
[See #37 73 -W]
Chic Bowdrie, you used the term CAGW. This means you lose the argument immediately. Thanks for playing.
That Chic can not acknowledge that radiation is the only way possible for energy to transfer from earth to space means that he has no argument to make.
And before you reply, Chic, think about what the words "to space" mean. It's key to understanding the greenhouse effect.
Hint: it doesn't take place at the surface.
"Chic Bowdrie, you used the term CAGW. This means you lose the argument immediately."
Brooks' Collorary to Godwin's Law? I like it …
I don't see how #37 has anything to do with my comments. [Sorry, I meant 73. The rest, as before -W]
Chic
"However, I doubt that a photon from a cold object will raise the temperature of a warmer object."
In that case you can discuss the problem with William's model *without* the need to deflect the discussion (as others have don) by referring to all the other important processes in the atmosphere.
W: Do you censor opposing views because
[repetition is tedious and valueless? Yes. But if you have something new to say, that will be fine -W]
“However, I doubt that a photon from a cold object will raise the temperature of a warmer object.”
Magic energy!!
x + 0 = 0
Eli, more like:
x + 0.99x = x
Eli, Pete, et al.,
How does a warm object avoid loosing more energy to the cold object that it receives a photon from in the same time frame?
[Um, well. You see the equations I've written down? Those are the answer to your question. If you don't understand them, then you don't know what is going on. If you don't know what is going on, then you need to stop, and go back to a level that you do understand, and build up to where you can actually say something about the subject to hand. Its better to do that than to insist loudly that your misunderstanding of the problem shows a fundamental error in well known science.
Or, you can do it in words: your "warm object avoid loosing more energy to the cold object" shows your error: you're thinking only of heat exchanges between warm (sfc) and cold (atmos). You're forgetting the energy input from the sun -W]
[Burrowed -W]
Probably the way you want to think about this is that the back radiation from ghgs slows the rate at which the surface is cooling.
Chic, "How does a warm object avoid loosing more energy to the cold object that it receives a photon from in the same time frame?"
There is also energy output to cold outer space.
A hot sun warms the earth. The earth warms the atmosphere. The atmosphere loses heat to cold outer space.
Similar to #84 if you reduce the rate the atmosphere loses heat to cold outer space (by adding CO2, say) what happens to this energy?
How does a warm object avoid loosing more energy to the cold object that it receives a photon from in the same time frame?
The surface does lose more energy to the atmosphere than it gains in back-radiation from the atmosphere. But it gains something and something is more than nothing.
Case 1: You give me ten dollars. I give you back two.
Case 2: You give me ten dollars. I give you back none.
Do you see any difference between those two cases?
Now replace the word "dollars" with the word "photons".
@Chic #83
1. The cooler object is emitting fewer photons per second than the warmer object.
2. The cooler object is emitting photons that, on average, have a lower energy (hence a longer wavelength) than the photons emitted by the warmer object.
NB: The cooler object is not reflecting back the photons it receives from the warm object, it absorbs them and emits its own -- at a lower rate and with a lower average energy. Likewise, the warmer object is not reflecting back the photons from the cooler object, it absorbs them. Using watts per square metre in radiated energy transfer calculations is much more practical than using individual photon transfers.
Hypothetical example of radiative heat transfer...
I'm out in space, billions of miles away from a star, when my spacesuit suddenly rips open and detaches. My skin at 33°C is radiating 500 watts per square metre. Would it help if I had a 0°C spacecraft to shelter in while I repair my spacesuit? The spacecraft would irradiate me with 316 watts per square metre thereby reducing my net heat loss to 184 W/m^2, which would be tolerable if I worked quickly on repairing my spacesuit.
I hope the above has illustrated that cooler objects do indeed transfer a lot of heat to warmer objects via radiation.
For anyone who wants to learn more there's a free online MIT edX course Global Warming Science which just started last week. You can register up until March 12.
Sorry correct link is https://www.edx.org/course/mitx/mitx-12-340x-global-warming-science-1244
At Pete #87,
In either case, I'm colder than before. Not warmer.
A cold object cannot increase the temperature of a warmer object without some third-party heat source.
[See my response at #83. Also, please think. Everyone else: can I ask you to stop pointing out the bleedin' obvious to CB? If he hasn't got it yet, he's doomed, so just give up. Please -W]
Well we could always pledge to not allow folk like him and Eli's current lil richard to post unless they let Victor and ATAP do so.
But I think Chic *has* got it.
This
"A cold object cannot increase the temperature of a warmer object without some third-party heat source."
implies this possibility:
"A cold object can increase the temperature of a warmer object with some third-party heat source."
[Well spotted; nice inversion. You are correct; lets hope Chic is capable of realising that he was correct -W]
So true
Re #32
The equations are based on an incorrect initial assumption that the troposphere would be isothermal if it were only pure nitrogen and oxygen. It would not be because, if it were then the kinetic energy of molecules would have to tend towards being homogeneous, whereas every time a molecule happened to have any upward component in its free path motion just after a collision, it would have to start creating the extra gravitational potential energy out of nothing because it cannot use up its kinetic energy.
Re #34
"No, I'm afraid you haven't even attempted to show how my process violates the SL"
I did so two years ago in my peer-reviewed paper "Radiated Energy and the Second Law of Thermodynamics" (linked above) published on several website in March 2012.
[If you mean http://tallbloke.wordpress.com/2012/03/13/doug-cotton-radiated-energy-a…, that's just words, and they appear to be a repeat of your misunderstandings above. If you mean the linked http://tallbloke.files.wordpress.com/2012/03/radiated_energy.pdf, that's a 404. Maybe TB got bored with the slayers? You might want to have a word with him -W]
FYI - William Connolley your "response" is a little out of date.
Thursday, 20th February, 2014,
Major revisions / rewrite again today..
I will continue to improve the piece, which has changed significantly since your post here was written, in light of responses I am aware of.
[You've stripped out some of the redundant pictures. You still, critically, have the wrong numbers on though. For "Model type 2" you say explicitly "One is supposed to follow the diagram from left to right. ie, arrow 1, arrow 2, arrow 3 and then arrow 4." This appears to be your key error - you think the arrows happen sequentially in time. But as I said, they don't. I'd rather hoped that you'd be able to read and understood what I've said -W]
Those with nothing better do to might enjoy looking into
http://soylentnews.org/article.pl?sid=14/02/27/2333227
(soylent news -- "it's people!")
developing as a replacement for the late lamented slashdot
William, you will find that David Archer does explain GH "theory" in the stepped manner I describe. As do many, many others. As have many, many others.
http://www.youtube.com/watch?v=8-5PsoF7Vp0
I have no doubt too that the way it will be explained in the future will have to change... and not just in the way you describe.
[No. He just writes the arrows down in that order. He could have written them down in any order. You've fundamentally misunderstood what is going on. This is an equilibrium viewpoint, not a time-dependent one. I don't know how to say that any more clearly. I think it will be too embarrassing for you to admit your error, so I suspect you're doomed to continue to insist on it.
Notice that he explicitly states (~18:00) that everything has to balance, which is an explicit contradiction of your picture. And then at 22:30 he explicitly (and correctly) writes down the budget for the ground, which doesn't agree with your (incorrect) budget. His budget only makes sense if the equations are not sequential. This is a very basic point, and cannot but be obvious if you understand the equations he is writing down.
At 33:05 he writes down Tg = fourth_root(2) * Ta, again in contradiction to your version -W]
> I have no doubt
There's your problem.
You're not doing science.
William, I state,
"Model type 3 - A 2PP very simple global energy budget.
Four arrows. Arrow 2 = 480W/m2
David Archer has shown above why the diagram should be read as arrow 1, arrow 4, arrow 2, and arrow 3. Plainly it is false logic.
In this model the atmosphere is depicted as having been warmed to 480W/m2, ie, 30C, by earth's surface which is according to the "theory" on average 30C.
In fact, this model type is a completely different type of model, it depicts energy flows or fluxes, not heat flows. This sounds a trivial difference, but it is not.
An energy flow is not necessarily a certain temperature, nor does it necessarily indicate a certain temperature.
Energy is the ability to do work, whereas heat is only one of the ways by which energy can be moved around."
In other words, yes, I do understand the stepped structure the various model types are explained in. AND, I accurately describe it.
BTW - It is not me doing the "science" it is me describing how GH "theory" advocates do the pseudo science.
Big difference...
Oh lord. Derek, energy is NOT the ability to do work. Heat is a form of energy, work is a form of energy. Work can be 100% converted into heat but the amount of heat that can be converted into heat is limited by the second law.
So, sadly, Dereck, you do not understand.
but the amount of work that can be converted into heat is limited by the second law.
Eli Rabett
http://rabett.blogspot.com
2014/03/02
"Oh lord. Derek, energy is NOT the ability to do work."
http://physics.about.com/od/glossary/g/energy.htm
"Definition: Energy is the capacity of a physical system to perform work. Energy exists in several forms such as heat, kinetic or mechanical energy, light, potential energy, electrical, or other forms."
I could change the word ability to capacity. How's that Eli? Does not change the meaning of what I wrote though.....
> A person inside a survival blanket is ... in an environment at
> the same temperature as their skin: 33°C. From outside the
> blanket,... its equivalent temperature appears to be same as
> that of the environment.
Wait. What?
... Its easy enough to fold the emissivity into the model if you want to, but it complicates the maths a little and it doesn't add anything fundamental to the solution. ...
Doesn't it make the amount of surface warming depend on the thickness of the atmosphere?
[Well, strictly dependent on the emissivity, but you can think of it as the thickness maybe -W]
And thus explain how adding greenhouse gasses to the atmosphere will produce surface warming.
[Only a bit, because (all together now) its a little bit more complicated than that. Looking up from the surface, the atmos is already opaque in the LW, except for windows regions. The emissivity only changes higher up. Etc. So, yes, you can add something to the model that looks somewhat like the effects of adding GHGs, but only a bit -W]
hmm, Derek, see the second sentence, although the entire thing is a train wreck. Heat is energy, etc.
#104: Eli Rabett
"but the amount of work that can be converted into heat is limited by the second law."
And here I thought it was the amount of heat that can be converted into work.
it was late....
... Only a bit, because (all together now) its a little bit more complicated than that ...
Um, this is a model in which the surface is at an uniform temperature.
And if you add emissivity then you can split the atmosphere into layers in a sensible way.
[Burrowed. You've said all this before, and you're becoming spam -W]