Atom by Atom Interaction: "Direct Measurement of the van der Waals Interaction between Two Rydberg Atoms"

I'm always a little ambivalent about writing up papers that have also been written up in Physics: on the one hand, they make a free PDF of the paper available, which allows me to reproduce figures from the paper in my post, since I'm not breaking a paywall to do it. Which makes it much more attractive to write these up. On the other hand, though, they do a pretty good job writing accessible descriptions, so there's not that much for me to add.

In the case of this paper, I'll write it up anyway (albeit somewhat more briefly than usual, because they already did a nice job), just because the concept here is so cool. For all that modern politics is a sucking swamp of awful, living in the future continues to be pretty amazing in terms of the science.

Dude, I don't have any idea what you're talking about. I mean, I look at that title, and I see "Direct measurement of jargon jargon technical term mumble." What's so cool about that? Well, it is a bit of a vocabulary test, I'll grant that. But if you know what the terms mean-- or at least can hold off your attack of the vapors long enough for me to define them-- the concept is pretty awesome.

Oh, all right, let's hear what all these weird words mean. Thanks for your vote of confidence...

So, the thing they're after here is a force called the "van der Waals" interaction, which is a tiny force between two neutral objects-- atoms, molecules, surfaces, whatever. This force is very weak, but also very important in a lot of phenomena-- interactions between atoms or molecules in vapors and fluids, and even adhesion between surfaces-- they specifically cite gecko toes as an example.

Stop right there. How do you have an interaction between neutral atoms? I understand static electricity and magnets, but I thought the whole point of neutral atoms was that they don't interact? They don't interact very strongly, but if you think about it, those neutral atoms and molecules are made up of charged particles, which interact electrostatically.

It's easiest to see with atoms. At any instant, you can (very roughly) imagine an atom as a positive nucleus with a negative electron somewhere outside it. Because they're not at exactly the same position, the electric field they produce doesn't cancel out perfectly everywhere. Technically, it's a "dipole" which just means (loosely) "a positive charge close to but not on top of a negative charge," and produces an electric field pattern that looks a lot like the classic "iron filings over a magnet" pattern. At a point somewhere on a line drawn through the midpoint of the dipole, perpendicular to the axis between the two charges, there's a force on a charge that's not directly toward or directly away from the dipole, but parallel to the axis.

Which makes iron filings line up with it? Well, this is an electric field, not a magnetic one, so we'd say that a positive charge at that spot gets pushed in the direction of the field. But that's the right basic idea.

You see, if you put a second atom at a point on that line, the small field from the first will push the electron in the second atom in one direction, and the positive nucleus in the opposite direction. Which tends to line those two up with the field from the first, making them another dipole. Which produces its own field, which then acts back on the first atom, producing a force that attracts them together.

So, wait, neutral atoms are attracted to each other? But if that's true, why don't we stick to everything? Well, to some degree, you do. But the van der Waals force that comes out of these interactions is extremely weak, and drops off very rapidly with distance. When you go through the math, it turns out to drop off as the sixth power of the separation between the atoms, so if you double the distance between them, the force drops to 1/64th of its original value.

That's... really small. But this is real? Oh, absolutely. There have been lots of measurements of van der Waals forces between different objects. You can work out what the strength of the interaction has to be from looking at bulk thermodynamic properties, you can look at the way atoms bounce off surfaces and determine the force from that, and lots of other tricks. What nobody's been able to do, though, is to take two neutral atoms, plunk them down at a set distance, and measure the strength of the interaction between them.

So, what's this paper, then? They took two neutral atoms, plunked them down at a set distance, and measured the strength of the interaction between them.

But... I thought you said you couldn't do that? No, I said nobody had done it. These guys just did.

But if the force is really small, and drops off really quickly, how did they do it? Well, with the other technical term from the title, Rydberg atoms. These are atoms excited to really high energy states, much higher than the ordinary states we deal with.

Define "really high." Well, if you talk about the simplest atom, hydrogen, the lowest energy state gets assigned the number 1, and transitions in the visible region of the spectrum generally involve atoms moving between states 3, 4, and 5 and state 2. People start calling them "Rydberg atoms" when you get to states with numbers around 20 and up. In this specific case, they used numbers 53, 62, and 82. Now, in rubidium, the lowest state starts at 5, but that doesn't make much of a difference here-- these are highly excited atoms.

And that helps... how? Well, the van der Waals force is ultimately due to the dipole character of the neutral atoms, which gets stronger as you separate the charges more. Higher energy states, roughly speaking, correspond to pushing the outermost electron farther away from the nucleus, so these highly excited Rydberg atoms are much more dipole-ish, which means the van der Waals forces between them get bigger. Dramatically bigger, as it turns out.

So, that makes the force big enough for them to hold one atom in each hand, and measure the tug between them? Well, no, because in that case what you'd mostly measure is the force between the hands. If you want to measure the force between single atoms, you need them to be isolated in space with nothing else around, which they accomplish here by holding each atom in its own optical trap. They take two laser beams, focus them down to small points a known distance apart, and trap one atom in each focus.

But how do they measure the force? By how much laser power they need to keep the atoms apart? No, though it's a good effort. What they do instead is to look at the energy of the two, and how the interaction affects their ability to excite the Rydbergs in the first place.

OK, what? Well, when two things interact, one way to describe it is as a change in their energy. So, the van der Waals interaction shifts the energy states of the two interacting atoms. But the way you create those interacting atoms in the first place is by using a laser to excite each atom from the ground state up to the Rydberg state, which requires a laser frequency that matches the energy difference. If the van der Waals interaction changes the energy, then at some point, the laser doesn't work any more, and you can't excite both atoms to the Rydberg state.

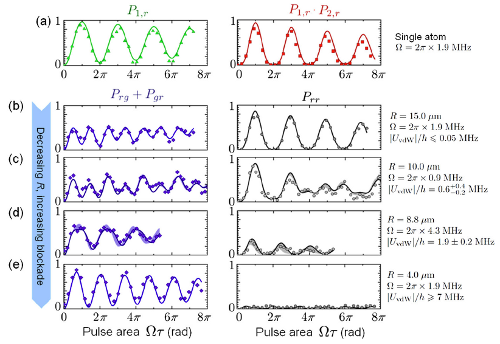
That's what they measured in this experiment, in the rather complicated figure that's the "featured image" above, which I'll reproduce here so you don't have to scroll back and forth:

Figure 2 from the paper described in the text.

What they're plotting in each of these sub-graphs is the probability of exciting atoms to the Rydberg state (number 62, though that's not critical). The left column is the probability of one of the two atoms being excited (technically the combination of the probability of finding one in the ground state and the other in the Rydberg state plus the probability of the one in the Rydberg state and the other in the ground state). The right column shows the probability of finding both atoms in the Rydberg state.

The graphs at the top with red and green data points are for single atoms, where they only loaded one of the two traps. The four graphs below, in blue and black, show the probability for progressively smaller distances between the two traps, from 15 microns down to 4 microns separation. If you look in the right-hand column of graphs, you can see the "blockade" effect from the van der Waals interaction shutting the excitation off: at large separations, there's a substantial probability of both atoms being excited, while at small separations, that probability is basically zero.

There's some complicated stuff going on in the left-hand column, but they understand what it is pretty well-- the solid curves are fits from a theoretical model, and agree quite well with the data. Using those fits, they can get the strength of the van der Waals interaction for each of the measured separations.

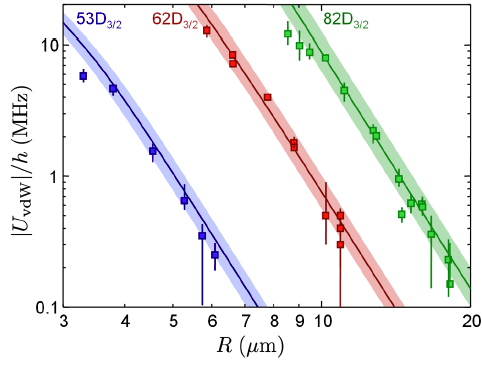
And when they do that? When they do that, for three different Rydberg states, they find results that agree beautifully with the theoretical prediction. Which they present in the following graph of van der Waals strength versus distance:

Figure 3 from the paper described in the text.

The points here are their measured values, and the solid lines are the theoretical prediction. The key statement about this is a phrase that warms the heart of any physicist: "without any adjustable parameter." That is, these aren't fits where they tweaked things to match the data: they calculated what the strength of the interaction ought to be, and drew a line on that basis, and the line agrees beautifully with the data.

So, this is what they mean by a direct meaurement of the van der Waals force? Yep. And that's what I mean by living in the future being awesome: we've got to the point where we can measure essential interactions atom by atom: putting two atoms a set distance apart, and directly measuring the strength of their mutual interaction. That's a great testament to both the advance of laser technology and the ingenuity of experimental AMO physicists.

I still think it'd be cooler if they measured the force needed to pull an atom out of the trap. But, you're right, this is pretty cool. Thanks. My pleasure.

Béguin, L., Vernier, A., Chicireanu, R., Lahaye, T., & Browaeys, A. (2013). Direct Measurement of the van der Waals Interaction between Two Rydberg Atoms Physical Review Letters, 110 (26) DOI: 10.1103/PhysRevLett.110.263201