Lots of folks have been asking me to write about φ, the golden ratio. I'm finally giving up and doing it. I'm not a big fan of φ. It's a number
which has been adopted by all sorts of flakes and crazies, and there are alleged sightings of it in all sorts of strange places that are simply *not* real. For example, pyramid loons claim that the great pyramids in Egypt have proportions that come from φ - but they don't. Animal mystics claim that the ratio of drones to larvae in a beehive is approximately φ - but it isn't.
But it is an interesting number. My own personal reason for thinking it's cool is representational: if you write φ as a continued fraction, it's [1;1,1,1,1...]; and if you write it as a continued square root, it's 1 + sqrt(1+sqrt(1+sqrt(1+sqrt(1...)))).
What is φ?
-----------------
φ is the value so-called "golden ratio": it's the number that is a solution for the equation (a+b)/a = (a/b). (1+sqrt(5))/2. It's the ratio where if you take a rectangle where the ratio of the length of the sides is 1:φ, then if you remove the largest possible square from it, you'll get another rectangle whose sides have the ration φ:1. If you take the largest square from that, you'll get a rectangle whose sides have the ratio 1:φ. And so on:

Allegedly, it's the proportion of sides of a rectangle that produce the most aesthetically beautiful appearance. I'm not enough of a visual artist to judge that, so I've always just taken that on faith. But it *does* shows up in many places in geometry. For example, if you draw a five-pointed star, the ratio of the length of one of the point-to-point lines of the star to the length of the sides of the pentagon inside the star are φ:1:

φ is also related to the fibonacci series. In case you don't remember, the fibonacci series is the set of numbers where each number in the series is the sum of the two previous: 1,1,2,3,5,8,13,... If Fib(n) is the *n*th number in the series, you can compute it as:

History
--------
There are a ton of stories about the history of φ. Most of them are utter bunk.
Many histories will tell you that the pyramids of egypt are allegedly built on the ratio of φ - nope. They're not. Many people will try to point of ratios of greek temples that are allegedly φ. Nope - that's just apophenia, like Gary Osborn and his 23.5 degree angles.
We do know that φ was identified by someone from the cult of Pythagoras - quite possibly Hippasus, our poor drowned friend from the history of irrational numbers.
It was well known by the ancient Greeks: Euclid write about it in his *Elements*; and Plato wrote about it in his philosophical works. In fact, I would argue that Plato is the initiator of all of the bizzare flaky metaphysical gibberish frequently attached to φ: he believed that the world was made of up four elements, each of which was formed from perfect polyhedra; the allowable polyhedra were built from triangles which included certain supposedly perfect ratios, foremost amont them the ratio φ. Thus to Plato, φ was one of the most fundamental parts of the universe.
The reason it's called φ is actually a reference to a greek artist who used it in his compositions; his name (lost in my notes) started with the letter φ.
After the Greeks, there wasn't a lot of interest in φ until the sixteenth century when a monk named Pacioli write a text called "The Divine Proportion", which discussed φ and its uses in architecture and art. Da Vinci studied Pacioli's text, and was fascinated by φ it ended up taking a major role in many of this sketches and paintings. In particular, his infamous "Vitruvian Man" sketch is his illustration of how the human body supposedly embodies the divine proportion φ.
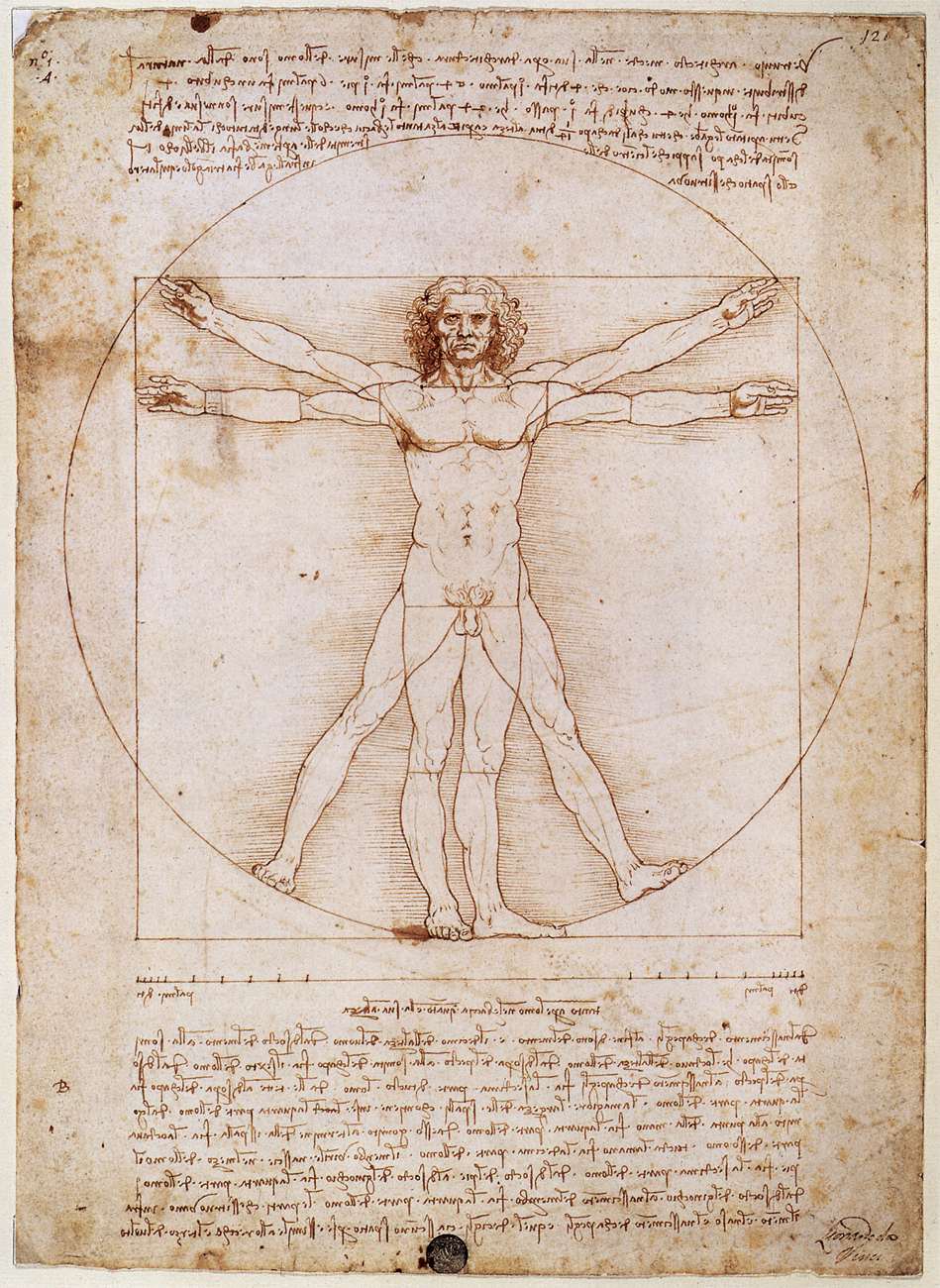
Of course, once Da Vinci embraced it, artists and architects all over Europe immediately jumped on the bandwagon, and it's pretty much continued to be used by artists and architects all the way to the present.
Unusual Uses of φ
-----------------------
φ does manage to show up in some astonishingly odd places. The basic scale used by western music is built on the fibonacci sequence - which, as I said above, is deeply related to φ. Several musicians have taken advantage of this; in fact Bela Bartok used it as a fundamental construct in some of his works, particularly the wonderful 12-part fugue in his "Music for Strings, Percussion, and Celesta".
You can build a number system called φ-nary on φ. The interesting this about this is that despite φ being an irrational number, every integer has a *terminating* representation in φ-nary; but every *fraction* has a *non-terminating* representation in φ-nary. Is φ-nary *useful* for anything? Not particularly, but it's pretty neat anyway!

Another aspect of Ï: it appears in many biological systems. This is due to the reiterative nature of the Ï ratio (as you point out, take a square out of a rectangle with the ratio Ï and you get another rectangle with a Ï ratio), and the reiterative nature of many biological forms (such as the spirals of the nautilus shell or the arrangement of sunflower seeds).
I believe the artist whose name gives us the letter φ for this constant was Phidias, whose work defines Classical Greek sculpture at its highest form, approaching --- dare I say it? --- the Platonic ideal of what Greek statues should be. (Obligatory Wikipedia link.) According to Larry Gonick's Cartoon History of the Universe, "Before Phidias, statues were stiff. After Phidias, they grew over-wiggly." (Quoting from memory, so it'll be approximate.)
According to MathWorld, "The symbol φ ('phi') was apparently first used by Mark Barr at the beginning of the 20th century in commemoration of the Greek sculptor Phidias (ca. 490--430 BC), who a number of art historians claim made extensive use of the golden ratio in his works (Livio 2002, pp. 5--6)." That Livio book is the following:
Livio, M. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books, 2002.
You didn't mention another *very* interesting little property about phi: Any power of phi is equal to the sum of the two immediately preceding powers. That is, phi^n = phi^(n-1) + phi^(n-2). Notice the similarity to the fibonacci sequence - this is why they are linked, iirc.
So, this implies two very fun little things. Phi + 1 = Phi^2, and Phi - 1 = 1/Phi.
Also, due to this, you can easy decompose any power of phi into multiples of phi and a constant. The multiple and the constant are always adjacent fibonacci numbers.
Another link between phi and fibonacci series - the ratio between two adjacent fibonacci numbers tends toward phi. This relationship is actually more general. The fibonacci sequence is a specific instance of the more general Lyer sequence (I believe it's called). A Lyer sequence is constructed exactly as the fibonacci sequence, where each value is equal to the sum of the previous two values, but it can start with any two numbers. So the Fibonacci sequence is a Lyer sequence starting with 1,1.
If you take the ratio of successive terms of *any* Lyer sequence, they will converge on phi.
You may also notice that the powers of phi are actually a Lyer sequence of their own, starting with 1,phi. The fact that the ratio of two successive powers of phi converges on phi is trivial, of course. Phi^n/phi^(n-1) is obviously just phi for all n.
The basic scale used by western music is built on the fibonacci sequence - which, as I said above, is deeply related to Ï.
I'm a music school graduate, and I had to look this up. I think you'll find that the fibonacci sequence shows up in music in much the same way that it shows up in pyramid construction -- as a post-facto rationalization using enormous fudge factors. You can model something like a scale using fibonacci numbers and pure intervals, but it's a purely hypothetical construct, of no real use outside experimental works. The modern equal-tempered scale (as on a piano) is actually based on intervals defined as the twelfth root of two. Singers, violinists, and other flexibly tuned instruments are constantly adjusting pitches subjectively, in reaction to other pitches and in accordance with learned esthetics of style. In the real world, single pitches and intervals are extremely fuzzy things.
You can make a better case for the appearance of phi in the proportions of large-scale Western classical compositions -- the climax of a sonata-allegro form usually occurs at or near phi/T, where T is the duration of the composition -- but then, classical composers were well aware of phi, so this is probably no accident.
Phi is interesting mathematically & shows up in some parts of nature, but aesthetically it has no special status -- it's like beauty of the Pythagorean musical scales: something that philosophers convince themselves of in order to infuse visual or musical art with some higher divine order. In reality, that stuff isn't especially appealing (which is not to say it's repugnant).
Two things:
a) I think you mean that phi=sqrt(1+sqrt(1+...)), not 1+sqrt(1+sqrt(1+...)) (which would be phi+1=phi^2).
ii) What do you mean by "the Western music scale is based on the fibonnaci sequence"? I was under the impression that it was based on the 12th root of 2...
Regarding my previous comment, the correct name is Lucas sequences, not Lyer sequences.
This is an immediate consequence of the fact that Ï is a solution to the quadratic equation x2-x-1=0.
One of those kooks who happened to wind up in a respected position is Dr. Atalay at Mary Washington College. He wrote a book, 'Math and the Mona Lisa' and spoke at my university to promote it. I knew he was full of it when he said that the ratio of the distance from a persons navel to the floor and their height was approx. 1/phi. Approximately? 1.5 is APPROXIMATELY phi. So we went back to our labs and measured the ratio for ourselves. 1.7, 1.4, 1.8, etc. It turned out he was off by ~25%, if I recall. A few other things he said turned out to be BS.
Hope that douche sells a lot of books.
Xanthir:
No need to wonder "i[y]rc." The relationship is pretty clear.
The same holds for any linear recurrence, and this is how you can solve for closed forms. Fibonacci sequences are given by the recurrence: Fn+2 = Fn+1 + Fn, which has the characteristic equation x^2 = x + 1.
This has exactly two solutions, phi and 1-phi. Integer powers of phi and 1-phi follow that same recurrence, and because it is linear, so do all linear combinations. The Fibonacci sequence is one of them. MarkCC gave the closed form above.
But if, for instance, you had the recurrence Pn+2=Pn+1 + 2Pn, you could set up its characteristic equation x^2 = x + 2, which has roots 2 and -1. If you set P0=0, P1=1, you get the sequence 0,1,1,3,5,11,21... Solve for the coefficients and you get its closed form: (2^n - (-1)^n)/3.
I'm not completely sure how you prove that every solution is a linear combination of powers of the equation roots (something to do with eigenvalues?). Here's a write-up on MathWorld: http://mathworld.wolfram.com/LinearRecurrenceEquation.html
Another nice algorithmic puzzle is how to compute the nth Fibonacci number in O(log n) integer multiplications (ignore that nice closed form). There are various ways to approach the question, but the one I always liked was based on expressing the Fibonacci recurrence as a matrix multiplication.
(Fn+2,Fn+1) = (Fn+1,Fn)M
where M=
1 1
1 0
That should be enough of a hint.
You can of course calculate any linear recurrence in similar fashion. I think this is also where eigenvalues come in, but my brain is very rusty in that department.
One more entry in my ongoing series of "Potentially Useful Links Posted to Other People's Blogs"! This time, I'd like to introduce everybody to an article by Keith Devlin entitled "Good stories, pity they're not true". It's a pretty good introduction to φ and the legend-memes which have grown up around the number. To quote the punchline,
Oops, I forgot to quote this part of Devlin's article:
Devlin's sources are the Livio book mentioned earlier and George Markowsky's "Misconceptions About the Golden Ratio", published in the College Mathematics Journal in January 1992 (Google Scholar).
Hugh Fraser (a British Columbian jazz musician) composed The Golden Mean Suite, inspired by the golden ratio.
http://www.hughfraser.com/hugh2.html (composer, performer)
(Producer: http://www.drborrie.com/bios.html -- to listen to a bit of it: http://www.drborrie.com/Sounds/Golden%20Mean.mp3 ).
Hundreds of millions of Europeans (and of others, I suppose) see this proportion on a daily basis: our printer/copier paper has these dimensions.
A0 is a poster; A1 is A0 cut in half; generally, A(n+1) is An cut in half (for any n). Our printers and photocopiers take A4.
Music is not based on Fibonacci numbers, but on integer proportions. 1/2 is an octave; 1/3, a fifth; 1/4, two octaves; 1/5, two octaves plus a major third; 1/6, two octaves plus a fifth; 1/7, a seventh; 1/8, three octaves; 1/9, three octaves plus a whole note. The human ear hears these intervals; the big intervals usually in low frequencies, the smaller intervals in higher notes (e.g. flageolets on strings, or harmonics you hear in wind blowing around a corner. Our music follows nature in this respect: lots of octaves and fifths in bass lines, smaller intervals in the higher parts. E.g. a major seventh chord (in C, that would be C E G Bb) is a very natural chord, being nothing else but the 1/4, 1/5, 1/6 and 1/7 harmonics of a (much lower) ground tone of 1/1.
So there are lots of proportions there but I do not see any Fibonacci.
In response to Reinier's comment: The A-paper sizes actually use the so-called silver ratio, sqrt(2)/2, which has the property that when a sheet is cut in two halves, both halves are in the proportion of the original. This can be expressed as 2b/a = a/b. Compare to the golden ratio, (a+b)/a = a/b, where one of the cut pieces is in the original proportion and the other is a square. Yay for equations which readily reflect their geometric interpretations.
It'd be fun if you expanded on using irrationals as a base, like phi-nary. I'd always expected bases to be natural or atleast rational numbers.
One aspect of phi that is most often overlooked is that Philadelphia starts with it, and almost ends with it.
You say they are all bunk yet give us no proof to disprove them. You can't claim something and then just leave it as you are the end all.
I wrote a short piece on Golden Ratio as well, it combines video with a light explanation of Phi, Uncertainity Principle and Chaos theory.
http://shuzak.com/Personal/Mathematics-In-Numb3rs.php
But anyway, there are many misconceptions surronding the Golden Ratio...some originating from Da Vinci Code. For example, the number of bees in a hive are not proportioed according to the Golden Ratio.
Again, thanks, all.
I was just thinking about those 'special' numbers again last night, like pi, e, and phi. The reason they're so special is just that they happen to be linked to very important facts. The number itself is arbitrary - it's the circle, or the growth, or the geometry that matters. The number just happens to be there.
I still find the numbers amazing, it's just always good to ground yourself every once in a while and remember *why* they're so amazing.
I'm supposing that φ-nary is pronounced "finery"? :-) All these numbers, dressed up in their finery...
For some links to phinary:
A lot of explanation, though not very organized.
The wikipedia entry on it.
Note - for the wikipedia entry, if you didn't get it immediately, a digit with an underscore is supposed to be negative. It took me a while before I understood how the example worked because of this - I thought it was equivalent to a digit with an overscore. >_<
In case anyone cares and it's not obvious, here's an answer to the algorithmic problem I mentioned above (how to calculate the nth Fibonacci number in O(log n) integer multiplications).
Start with: (Fn+2,Fn+1) = (Fn+1,Fn)M for M given above.
Then it's easy to show by induction that(Fn+1, Fn) = (F1, F0)M^n = (1,0)M^n, which is simply the top row of M^n. So if you can calculate M^n, you can easily get the value of Fn+1.
If n is a power of two, you can calculate M^n by repeatedly squaring the matrix. If n is not a power of two, you can represent it in binary as a sum of powers of two, and get M^n by multiplying those values. So, for instance, if n is 37, then n=32+4+1. Calculate M^2, M^4, M^8, M^16, M^32 by repeated squaring and then calculate M^32*M^4*M.
Of course, you don't need to do the full matrix multiplications. In fact, it is not hard to see that the matrices M^n always have the form:
a+b a
a b
So if you just want to know the values of a and b for M^n for some power of two, you can iterate using:
(a,b) := (a*a+2*a*b, a*a+b*b)
Applying this iteration a few times (all right, I used an Excel spreadsheet), we get (1,0), (1,1), (3,2), (21, 13), (987, 610), (2178309, 1346269), so the values of F1, F2, F4, F8, F16, and F32 respectively are 1, 1, 3, 21, 987, and 2178309.
In response to marcus' comment: "It'd be fun if you expanded on using irrationals as a base, like phi-nary. I'd always expected bases to be natural or atleast rational numbers."
What about natural logarithms? Base e. Last I remember, not only was e irrational, it was also transcendental.
I'm sorry that others enthusiasm for phi has turned you against it.
How come no one has printed out the first few digits of phi? 1.618033988749894 .... and more. Its delightful that phi - 1/phi = 1. And useful to quickly get a feeling for the limits of accuracy of whatever computing system you're working with. For the system I'm currently using 1.0-phi-1/phi = 1.11E-16.
One more point in defense of phi. If you need to find a root numerically between two values, a and b, you will proceed more rapidly to the solution if you choose test subintervals using phi (golden section) rather than 2 (bisection).
Xanthir notes that Phi+1 = Phi^2. A good visual confirmation of this is the image at the top of the page. The width of the larger triangle is Phi^2, and the widths of the two squares inside it are Phi and 1, thus Phi+1=Phi^2.
Similarly, if you look at the heights of the rectangles, you immediately see that Phi = 1+(1/Phi) (confirming Xanthir's other statement that Phi-1 = 1/Phi)
What software do you use for your various diagrams, BTW? Thanks.
justWondering:
I use OmniGraffle on the Mac for all of my diagrams. It's all around one of the best pieces of software I've used - incredibly powerful, witha fantastic, clean UI and tons of subtle contextual help for creating attractive diagrams.
Another interesting observation from the image at the top can be seen by calculating the area of the rectangle.
Imagine continuing the process of dividing the rectangles into smaller squares and sub-rectangles infinitely many times.
What you wind up with is a series of smaller and smaller squares with sides phi, 1, 1/phi, 1/phi^2 ...
The sum of the areas of this infinte sequence of squares will be equal to the area of the original rectangle.
The expression becomes:
phi^3 = phi^2 + 1 + 1/phi^2 + 1/phi^4 + ...
or
1 = 1/phi + 1/phi^3 + 1/phi^5 + ...
Maybe some people like the golden ratio ( and the whole myth around it ), because they believe they know a secret of the world.
ArmchairMathNerd:
That's a very interesting observation that you can also see when you represent numbers in phinary.
Because of the relationship Ïn=Ïn-1+Ïn-2, any time you find _011_ in the number you can change it to _100_. For example, the number 11.01Ï can also be represented as 100.01Ï. This is actually necessary to write phinary in 'standard form' - standard form never has two 1s in a row.
This runs in reverse as well, obviously. So, if you were to take, say, the number 1Ï, you could change that to 0.11Ï. This can be changed to 0.1011Ï, which can then be changed to 0.101011Ï, which can then be changed to 0.10101011Ï...
In other words, just like .999...=1 in decimal, .101010...Ï=1 in phinary. This is why that relationship you noticed in the diagram works.
"the fibonacci sequence shows up in music in much the same way that it shows up in pyramid construction"
Yeah I had to choke on that one a little too. The modern Western scale is 12 notes (chromatic scale) whose ratio is based in the 12th root of 2... which is roughly 1.0594630943593. So given the frequency of A (440 Hz), the frequency of A# is 1.0594630943593 times higher (rounded: 466.164 Hz).
There have been many "Western" scales, but that's a different contentious topic.
Speaking of music and math, I only learned very recently (well into middle age) that the black and white keys on the piano could be defined by a simple mathematical relationship. This is old news to anyone who has had even a little musical theory. Actually I have known since childhood that an octave doubled the frequency and that adjacent keys were the 12th root of two apart, but I didn't realize that the notes chosen for the standard scale could be generated using a simple formula in modular arithmetic.
To demonstrate this, you can generate white and black "keys" in an Excel spreadsheet as follows.
(1) Put this expression cell A1: =MOD(ROW(A1)*5, 12)
(2) Now copy-paste it down column A as far as you like.
(3) With conditional formatting, set all cells with values greater than or equal to 7 to black.
Now the black and white cells will be arranged like piano keys (you can introduce an additive constant to adjust the starting point).
This is just a variation on the well known "circle of fifths" from music theory. The reason (as I understand) that it is chosen this way is that you get (approximately) a fourth or fifth using keys that are five or seven steps apart respectively (note: 7= -5 mod 12). The white keys are spaced so that if you start with a white key you almost always get another white key five or seven steps away. It's easy to verify this if you have a piano or music keyboard handy.
If you pick some spot on a circle, mark it 0 and move 5 steps clockwise, mark it 1, five more steps, mark it 2, etc. you eventually fill up the circle. Now color the values 0-6 white and 7-11 black. This will also give you the pattern of keys on a piano, but it is easy to see that this is equivalent to the formula using modular arithmetic.
I apologize for the trivial music theory. Often people say that music is a good way to introduce kids to mathematics. I wish that conversely, somebody had used mathematics to get me excited about music at an early age, because it is something I sadly missed out on.
I just found this blog. Cool stuff.
I've been writing some on math for another blog. How do you format this for math? I've been typing in Word, adding formulas in MathEdit, saving the images to photobucket, and then pasting into the blog.
But I'd love to use LaTeX.....
Thanks
Peter:
I mostly use HTML entities for mathematical characters. When I can't avoid it, I do more complex equations in MathType, export them as images, and upload those. I'd like to use MathML, but I haven't been able to make it work so far with the ScienceBlogs templates.
TeX4ht has the ability to generate really gorgeous looking webpages with math, but it uses a mixture of MathML and embedded images, which makes it very painful to use for blog entries on moveabletype, which is what we use at SB. So you might want to look at that.
one of the absolutely most brilliant mathematical modeling proofs i have ever seen uses (completely unexpectedly) phi.
the problem is often called "conway's soldiers" because the proof (and possibly the problem) was john conway's. you can find it at:
http://www.cut-the-knot.org/proofs/checker.shtml
if you have never seen this problem, it's worth looking at. it uses pretty much only high school algebra, but it proves that a solution to a completely non-algebraic problem is impossible. just another good use of phi.
Mark:
Thanks. By HTML entities, do you mean raw HTML code? Any good bur introductory places on doing it?
More generally, I am looking around your blog and really like the material. I'm a data analyst, not a mathematician, but I like this sort of thing, and like educating the public about some neat math ideas.
My only problem now is that each blog i go to uses a different structure, so figuring out and rememebering the best way to navigate around each is a bit of a pain....
thanks for responding
Peter
Peter:
HTML entities are special syntax in HTML for characters that aren't part of the normal typable character set.
So, for example, to write ∀, what I'm actually typing is ∀.
There's a really good site with a list of the HTML character entities at: http://www.avenue-it.com/html/extracharacters.html
Xanthir:
That's very cool. Since your phinary scheme shows the results of recursively applying the definition of &phin = &phin-1 + &phin-2 to the &phin-2 term, the obvious thing to try next is recursing on the &phin-1 term, and then of course on both terms.
Doing the recursion on the &phin-1 term winds up showing off the Fibonacci series in interesting ways, as was noted earlier.
Recurse on every term and Pascal's triangle starts to emerge. You get an infinite number of expansions of this form:
Sum[Binomial[n,j]*phi^-(n+j), {j, 0, n}] == 1
where n is the nth row in Pascal's triangle.
(you can use http://www.mathmlcentral.com/Tools/ToMathML.jsp to convert the expression above to Mathml and to render it as a gif)
he believed that the world was made of up four elements, each of which was formed from perfect polyhedra; the allowable polyhedra were built from triangles which included certain supposedly perfect ratios
History of science check, here. Plato believed that the traditional four elements were characterized by--not made up of physically of--four of the Platonic solids. You know--cube, tetrahedron, octahedron, icosahedron. The fifth, the dodecahedron, he identified with the cosmos as a whole (because it's sorta-spherical, as the ancient Greeks believed the universe to be).
Three of those Platonic solids are made up of equilateral triangles; the cube is, of course, made up of squares, and the dodecahedron has pentagonal faces. You tell me if phi is present somehow in those figures, or other irrational numbers, but Plato was as good a geometer as he was a geometrical mystic, and the main reason he cared about them (and the reason we call them Platonic solids) was their intrinsically interesting geometric property (which I assume everyone here is already familiar with).
I am not a mathmatician, but an art student who was asked to research the golden ratio. I have recently written a manuscript called N3 (N to the 3rd power) It is divine and inspired. It wasn't until I started researching golden ratio that I realized the reason it baffles you mathmaticians is because it truly is divine. If we could just take a moment and stop trying to solve the equations of the earth around us and the stars and the moons, then maybe we will finally come to the conclusion that we need to seriously investigate the human heart. It is Gods creation, literally and the feelings of love and emotion that dwell there can literally lead us to the greatest treasure I have ever found. It is an actual place!I know each person must find this place themselves, but I do want desperately to help others find it. Once you find it everything makes sense. Naturally the golden ratio and Pi are Gods theories, his equations. You are all amazed at how it is used in music, Davinci's paintings, codes, the human face, nature, biological sequences, well I want to testify to all you men and women out there that think they have a masterful brain that you DO! God created it and his brain is incomprehensible, so quit trying to figure out his theories on your own intellect, visit him through prayer and search the scriptures. All the answers are there. Read Revelation 20 and 21 where you will find that there is a place the is foursquare (a cube-like structure) where the children of God will enter and dwell with Christ. The earth will be cleansed by fire and be like a sea of glass, a crystal ball. Isn't the golden ratio cirle with its triangles and pentagon like a crystal ball? Imagine it spinning like the earth. I cannot explain further. It sounds a bit complex, but makes total sense to me because I am his creation and his mind inspires mine. Thank you for reading. Debbie Jones
Timecube?
Re: #43 I'll wait for the movie of The Da Vinci Timecube.
Re: #42 "... the dodecahedron has pentagonal faces. You tell me if phi is present somehow in those figures..."
Phi comes up several times, with lots of nice pictures and equations, at:
Weisstein, Eric W. "Dodecahedron." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Dodecahedron.html