Yesterday's Wall Street Journal has a *spectacular* example of really bad math.
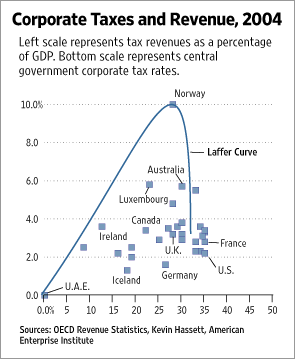
The WSJ is, in general, an excellent paper with really high quality coverage of economic issues. But their editorials page has long been a haven for some of the most idiotic reactionary conservative nonsense this side of Fox News. But this latest piece takes the cake. They claim that this figure is an accurately derived Laffer curve describing the relationship between tax rates and tax revenues for different countries; and that the US has the highest corporate tax rates in the world.
There's an idea in economics about taxes called the Laffer curve, which is based on the extreme value theorem. What the Laffer curve describes is the relationship between tax revenues taken in by the government and take rates. Naively, you might assume a linear relationship between taxes and revenues: raise the tax rate, and the amount of money that the government brings in increases.
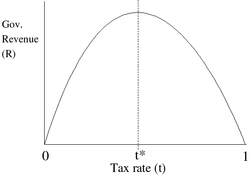
But reality isn't so simple. When you increase tax rates, you reduce the amount of money available to people and businesses for investment. So it's not a simple linear thing; the size of the pool of taxable profits can be altered by changing the tax rate, because a higher tax rate reduces the amount of money that can be invested in growing a business, which can slow the growth of the business, which reduces its taxable profits. The Laffer curve is a model for the relationship between tax rates and tax revenues. It starts off roughly linear, and then the revenue growth rate starts to slow, until it reaches an inflection point, and revenues start to *decrease* as tax rates increase. The figure to the right is a drawing of the standard Laffer curve borrowed from Wikipedia.
What people like the WSJ editorial page like about the Laffer curve is that one of the implications of it is that if your tax rate is *past* the inflection point, then you can *increase* tax revenue by *decreasing* the tax rate. So they constantly argue that our tax rates area on the downward-trending side of the curve - and that therefore, lowering takes isn't just good because it means that people get to keep more of their money, but it's in some sense free, or even *better than* free, because it will have either no impact or a positive impact on government revenue.
The catch, of course, is that for that to be true, you need to be on the far side of the curve, where revenues are dropping because the rate is so high that it's stifling investment. The WSJ editorial board constantly argues that we're on that side. And they argue it in stupid, sloppy ways.
Which brings us to the subject at hand: the WSJ's latest effort to support their argument that we're on the wrong side of the Laffer curve. They take a scatter plot of tax revenues as a percentage of GDP against take rates for a selection of countries, and then argue that it's an illustration of the Laffer curve. The thing is, it's more of a laughable curve than a Laffer curve. If you look at the data, what you see is a scatter that looks an awful lot like a typical noisy linear curve. It's got one extreme outlier, which the WSJ chooses as an inflection point, and then they curve fit on either side. The resulting curve is blatantly ridiculous - the tax rate smoothly increases in an almost linear way up to almost 25%; slows to crest over about 3%, and then falls into an almost perfectly vertical line over the next 4%. It's a terrible curve fit, which is just simple foolishly wrong.
In fact, it's an example of the same kind of nonsense that I wrote about in the very first post on the original GM/BM back at blogger, where the Geiers were analyzing autism rates, and *wanted* to show an inflection point, so they inspected the data, picked an outlier, split the data around it, and then argued for an increasing slope on one side, and a decreasing slope on the other, even though a single linear regression with a shallow increasing slope matched the data better than the double-curve with their chosen inflection point.
That's exactly what's going on here. For *some* reason, Norway is an extreme outlier in this data. Eliminate Norway, and you've got data that looks awfully close to either a nice linear slope, or to a very shallow Laffer curve. But drawing the curve not as any reasonable mathematical curve fit, but instead building it specifically to pivot on the outlying point, they've created an artificial and ridiculous curve. Sure, it supports what they're arguing for: it was artificially and dishonestly created to do exactly that.
Here's an interesting fact, which the WSJ folks certainly know about. In mathematical curve fitting, where you try to use some kind of regression method *honestly* fit the curve to data, you *never* wind up with a curve that intersects the most extreme outlier. The fact that this curve does just demonstrates its dishonesty.
The data underlying this is also definitely not honest. Calling the US corporate tax rate 34% without any qualification isn't honest at all; it neglects to mention the fact that the US has one of the most ridiculously loophole-ridden tax codes in the world, and that the actual average rate actually paid by American corporations is dramatically lower. (Just for example, the WSJ cites the average state tax rate at 4%; actually statistics show that the state rates really paid were under 2.5%, and the larger the business, the lower the rate they paid. In 2003, for example, Boeing and ATT paid *no* state taxes *at all*.)
I don't know where we fit on the Laffer curve. Frankly, I think our tax code is so distorted by random loopholes that it's probably impossible to make a blanket statement; for some businesses, we're probably taxing them enough effectively reduce the tax revenues received from them; for many others (can you say oil company?), we're clearly *not*.
But the idea that this curve produced by the WSJ folks has *any* meaning at all is simply laughable.

Ugh... Since when is the AEI considered a reliable source of data anyway?
The economics blogs suggest that Norway is an outlier because of oil revenues. Other oil rich countries either have low tax rates or are not very dilligent at corporate tax collection.
Not to mention Norway's huge ($300 billion +) investment stash (http://en.wikipedia.org/wiki/The_Government_Pension_Fund_of_Norway) which might throw things off a bit.
umm - do a global search and replace: replace "inflection point" by "extremum". The curve as drawn has no inflection point.
Give them credit for being clever.
When I first heard of the Laffer curve in the news decades ago, the news coverage never explained what it was.
Your article is the first description of what the curve is.
Thanks much. Now I know what all that blather was about a quarter century ago.
until it reaches an inflection point
You mean a maximum, right?
I wouldn't quite say that it's linear when you leave out Norway. There seems to be a maximum at somewhere around (30%, 4%) -- I think that for tax rates between 30 and 35% I see the points tending downwards. (And I am sufficiently ignorant of economics that I assure you I am not grinding any sort of ideological axe.)
Of course, trying to fit a curve mathematically to this plot can't be done unless you know ahead of time that the curve should be, say, quadratic -- and we don't know what shape it should have a priori.
Isabel -- I noticed the same hint of a turnover, but I think it's probably just a mirage. Jiggle all the data points half a tick in a random direction, and that peak would disappear!
Incidentally, curve fitting is something that's been on my mind lately. A few days ago at work, I made a plot that looked *very* much like a power law with an exponential cutoff, but a power law without a cutoff fit it just as well. I'm beginning to suspect that without an a priori model, fitting isn't any use at all... :P
Pardon me if my question sounds extremely naïve, but can't that be simulated? Isn't it possible to build a reasonable model illustrating the Laffer effect, and helping to determine where the inflexion point is, according to a few key parameters?
I guess my question could be rephrased as: in these days where we attempt to model cimate change, building a model showing that the Laffer curve is for real, shouldn't be that difficult, should it?
By the way, hello from ... Norway, the country of the tax optimum (uh?).
"You mean a maximum, right?"
No, I suspect he means a point where a curve alternates concavity (upward/downward), i.e., a point of inflection.
Correction: even with Norway you've got data that looks awfully close to either a nice linear slope. It might be slightly heteroscedastic, but it still looks linear (and adding the quadratic term in the regression increases the R2 by less than 0.2%).
Bob
If they placed the inflection point around, say, Australia, it might look half-reasonable and BS'able.
I think the point is being missed here. The WSJ should be challenged to provide the R^2 values for their curve and a linear regression curve. I will bet the ranch that their curve will have a significantly lower value then a linear regression.
I thought the same thing when I read it.
But the function doesn't change concavity; It's derivative is always decreasing.
The WSJ and other "supply side" minions would use graphs in the shape of Sesame Street's "Cookie Monster" if they thought it would help cut taxes on their corporate buddies and the super-ultra-mega wealthy.
The theoretical maximum of the beloved Laffer curve is, I would hypothesize, very, very simple to determine: it is far closer to zero (or negative taxation, why not?) of whatever tax rate corporations and the super-rich find themselves at present.
So if today's tax rate were 10%, that maxima would be at, who knows, 2%, and if today's tax rate were 2%, then that maximum would be at 0.05%, and if today's rate of taxation of corporations and the super-wealthy were at 0.05%, then the WSJ editorialists and pals would argue that ideally their tax rate should be at -2%, where the rest of us pay them dividends simply for being so wealthy.
And don't forget Martin Gardner's Neo-Laffer curve, from his Scientific American column many years ago. Martin accepted the two endpoints of the curve, where zero or 100% taxation will obviously drive revenue to zero. But anywhere in between, any real economy will be so complicated, non-linear, and chaotic that it is absurd to draw _any_ simple-looking curve. The real curve, says Mr. Gardner, would have quite a collection of valleys and peaks of varying sizes - and good luck predicting where the myriad rises and falls will be. Here's Martin G.'s Neo-Laffer curve:
http://ase.tufts.edu/cogstud/graphics/tempfig4.gif
Seeing where the US and France are according to the WSJ "Laffer curve" it seem like an infinitisimal tax decrease would give a fantastic increase in revenue. However, I suspect that the authors argue for a somewhat larger reduction than that. So, their ridiculous curve doesn't even work very well for their arguments' sake.
Isn't it also possible that the curve isn't being derived from the data, that the shape of the Laffer curve is being asserted on some other grounds and the points are just to show where various nations are in relation to it?
And yet by some coincidence that theory which dare not speak its name produces a point exactly on Norway?
As always, Mark hits the nail on the head: someone *wanted* to see a Laffer curve, looking at data points that, in essence, look like a bowl of tea leaves. But the textbook predicts a curve, so a curve it shall be. This is the kind of situation statistics thrives on. And whenever statistics is involved, I'm never sure if the lying is deliberate.
I wonder what function they used to give that steep drop-off? Of course, if you look at the data, you end up concluding that any functional relationship between the tax rate and revenue only explains a tiny part of the variance, so you might as well forget about the Laffer curve as a guide to tax policy.
"But the function doesn't change concavity; It's derivative is always decreasing."
I don't see how the derivative can always be decreasing, the tangent line on the curve would have to alternate direction at some point. But as the above poster noted, it's difficult to even discern the function they're using by simply looking at the graph.
Although the tangent (and hence the derivative) goes from positive to negative, there is no point where it is not decreasing.
An easy way to prove that the Laffer curve has no points of inflection is to notice that the tangent line never crosses the curve.
"An easy way to prove that the Laffer curve has no points of inflection is to notice that the tangent line never crosses the curve."
You're right, I accept the correction. I was thinking in terms of relative extrema and overlooked a simpler indication.
"I don't see how the derivative can always be decreasing."
Draw a line tangent to the curve. The derivative at that point is the slope (steepness) of the line. At the left the line is very steep and becomes less so as you move to the right. Since the line rises to the right the slope is positve at the left. At the peak the slope is zero. To the right of the peak the slope is *negative*. Positive to zero to negative-- always decreasing.
"Draw a line tangent to the curve. The derivative at that point is the slope (steepness) of the line."
As I mentioned the tangent line in my post, it should be obvious I already know this. I overlooked a more important detail.
Point 1: The graph is comparing total tax revenue to corporate tax rates. A more useful comparison would be to compare corporate tax revenue with corporate tax rates. Total tax revenue in France isn't higher than in the US because the nominal corporate tax rate is slightty lower - it's higher because personal income tax and value-added taxes in France are much higher.
Point 2: Nominal corporate tax rates are deeply misleading in any case because there are huge differences between nominal and effective tax rates depending on deductions and other aspects of the tax system. For example, in most developed countries, workers pay taxes to fund universal heath care. In the US, employers are given tax incentives to buy private health insurance fro their workers. Those tax concessions reduce the effective tax rate below the nominal tax rate.
Point 3: Virtually the only unambiguous evidence of a positive revenue effect from cuts in nominal tax rates comes from countries where the nominal rates were at 80% or greater. Claims that US tax cuts produced higher government revnue are based on conflating several different logical fallacies.
For example, we're told that tax receipts in 1987, after the Reagan tax cuts, were higher than in 1980. This is true in nominal terms - i.e. if you ignore the high inflation of the intervening period. Hell, if we lower taxes to 1% and just print a few hundred trillion dollars in fiat money, we can probably produce an even higher increase in nominal tax revenue.
Australia and Luxembourg are also anomalous outliers.
Here in Australia we've been incredibly fortunate over the last years in that the commodities boom has delivered a massive profit boost to our mining companies.
Luxembourg is a relatively low tax country within the EU and attracts large investment inflows from Germany and other countries. The country is also an attractive legal residence for European companies (American readers should be familiar with te expression "A Delaware company".)
I find it interesting too that the CEI and WSJ are apparently claiming that Canada and France are more business-friendly and entrepeneurial than the US. I doubt that's an argument they'd be making in any other circumstances.
Wait wait wait.... Taxes are higher in the US than in France or Germany? That doesn't sound quite right...
Ooh, as a professional statistician, do you mind if I fume at that for a moment?
The imposed Laffer curve is awful statistically: we have a huge suite of techniques for fitting curves to data like this: least squares, non-linear least squares, splines etc. etc. None of them would produce a curve like that with the data.
Most problems commonly associated with statistics are due to the people who are mis-using them. A lot of attention is paid to trying to prevent this sort of abuse: through statistical training, education of the public and other efforts (e.g. the Royal Statistical Society made a public statement on the Sally Clark case, because the evidence presented was so bad). We dislike things like this as much as everyone else does, and it doesn't help that we get the blame.
In reality, it's the economists who are the evil-doers. We're pure as the driven snow, and standing up for all that is good and can be counted! :-)
Bob
I have always wondered about corporate taxes. Corporations have so many write-offs that I'm not sure on what money they are even required to pay taxes off of. Aren't investments tax write-offs anyways? If a corporation has a huge operating margin but reinvests a large portion of it, doesn't that mean they only have to pay very little tax?
First of all, the x-axis shows corporate taxation. Secondly, the point for France is approximately on the same spot as the US on that axis.
Lies, damned lies and statistics, this looks like to me. Perhaps an article on how curves should really be drawn is in order?
I have worked as employee, contractor, or consultant for many corporations, often in the Software Engineering department, and on special projects for the very top executives, including:
Boeing, Burroughs, EarthLink, Ford, General Motors, Hughes, Lear Astronics, Systems Development Corporation, Yamaha.
There was enormous diversity in the politico-economic beliefs of the managers and executives that I worked with, as well as among the engineers and secretaries and others. But there is no question that the Wall Street Journal was as universally respected as Aviation Week and Space Technology (in the aerospace companies), and IEEE Computer or Communications of the ACM at the computer/software companies.
The management clustered around reverence for Capitalism in an unrestrained form (such as Taiwan has more than the USA). They appreciated the vast amounts of money that they were able to pry away from U.S. Army, U.S. Navy, U.S. Air Force, Federal Aviation Administration, and NASA, by means of Proposals that ran to 1,000,000 pages in length (and in which I was often deeply involved as writer, editor, or management Gold Team reviwer, or the like).
Once your tax dollars were in corporate hands, they were systematically plundered in what I best describe as ongoing criminal enterprises. The "Laffer Curve" invented during a 3-martini lunch at WSJ is benign compared to the frauds that I saw (and officially audited!) at these large corporations.
The corporations made routine use of the Revolving Door. They hired former government officials who used to shovel money to them, and used them to help get more. They sent former executives of the corporation to the government, to improve the efficiency ofd the shoveling. Once in a long while, someone was caught, and their hands were slapped. Sometimes the slap was more substantial, as with Boeing's multibillion dollar Air Force Tanker scam, or Rockwell's Rocky Flats dumping of plutonium in the Denver water supply, which got the installation shut down, and the employees not laid off with benefits, but somehow out the door with no benefits.
I have never seen any of the fraud perpetrators go to jail. I am still furious that nobody went to jail for the Challenger and Columbia tragdies, for instance, on Manslaughter.
Google "Mens Rea" for the reason embedded in US law as to why Corporations cannot be guilty of most crimes.
The Wall Street Journal was the bible of my grandfather, who worked his way up from floor sweeper at a haberdashery to founder of a stock brokerage and owner of a seat on the New York Stock Exchange. he was opposed to Unions, Taxes, and FDR for good reasons. But I think he'd be uncomfortable with such a blatant lie as the WSJ has printed here.
I'm not so much offended as a Mathematician, as I am offended as a Capitalist and a taxpayer and a former card-holding journalist.
Good thing that Rupert Murdoch doesn't own the WSJ. Why, he'd bias their news writing to achieve political ends and to line his and his friends' pockets with gold. Oh, just a second...
Speaking as a card-carrying PhD-emburdened computer scientist, I can say with absolute conviction that Communications of the ACM is the most useless, mind-numbing mixture of utter bullshit and meaningless corporate buzzworrhea ever produced outside the DC Beltway, with occasional homeopathic quantities of actual information to cut the stench.
So when you write that WSJ was as universally respected as CACM, I know exactly what you mean.
Bob O'H said: Ooh, as a professional statistician, do you mind if I fume at that for a moment? ... The imposed Laffer curve is awful statistically...Most problems commonly associated with statistics are due to the people who are mis-using them...We dislike things like this as much as everyone else does, and it doesn't help that we get the blame.
Indeed, whenever someone tells me that people lie with statistics, I remind them they lie with words too. Does that mean we dismiss the English language? To take what some say seriously, one would think in statistics classes the instructors told us to do whatever we wanted.
More to the point, I think it worth noting that while dittoheads chant like a mantra that Reagan's Laffer-inspired supply-side tax cuts "doubled revenues", I've never seen a rigorous demonstration of this. My own attempts failed, the claim only holding up prior to adjusting for inflation, after which the Reagan years were indistinguishable from the Carter years prior or the Bush 41 years to follow.
And now Republicans areo continue to make this claim, sans evidence, that Bush 43's tax cuts have done the same. Prove it I say.
While I agree that the "curve fit" is howlingly, atrociously bad, there is another significant problem with the WSJ chart -- it does not in fact present data by which one might evaluate a supply-side claim. Not even with a better model. Not even after excluding "outliers." The data just are not in the figure.
Mark's graph shows the Laffer curve as supply-side theory is typically portrayed: there is some optimal tax rate at which government revenue is maximized.
The horizontal axis on the WSJ chart is the top marginal tax rate on corporate profits, so it is not necessarily an accurate measure of the actual rate at which corporations' incomes are taxed. It's better than nothing, I suppose, but since these taxes are levied on profits, not on income, a country-to-country comparison is meaningful only if taxable profits are calculated the same way from country to country (which I strongly doubt).
Note further that the vertical axis on the WSJ chart is the tax revenue from corporate taxes as a fraction of GDP. (In 2004, total federal tax receipts were 16.3% of GDP, so the data presented for the USA in the graph cannot represent total federal tax revenues.) However, US government statistics for 2004 show that corporate income taxes were 1.6% of GDP, so there are other contributors to the numbers for the vertical axis. This again muddies the meaning of the plot.
But neither of these are, in my thinking, the biggest non-regression-related problem with the chart. They serve to make the meanings of the points fuzzy, but one might be sorta kinda able to spot trends if there are trends to be spotted.
The killer problen is that the vertical scale is tax revenue as a fraction of GDP; it says nothing about the size of the GDP or the amount of tax revenue received.
Thus, the relationship between the ordinate and abscissa values on the WSJ chart might tell us something about the relationship between taxable corporate income and GDP, but it tells us nothing about the relationship between government tax revenue and corporate taxation. It does, IMO, tell us something about the state of critical thinking skills at the WSJ.
A paper that Cosma Shalizi coauthored has a test that can distinguish between different alternatives here.
And no, curve fitting is of no use for these types of problems:
I would dearly like to take this method out for a test ride next time I have to navigate these types of problems.
On second thought, that was too harsh. Curve fitting should show you when a power law wouldn't fit at all.
Why would anyone believe that the Tax revenues were a function of a single variable?
(Tax rates). It seems ridiculous on the face of it.
Much more important than the rate is the how the taxes are spent: are they being used to improve the infrastructure, or are they being used to reward corruption?
The data points that we see would seem to indicate that if the tax revenue function were a function of one variable then it would not be continuous.
What it looks like is the graph of a function of several variables which some moron projected onto a plane spanned by one variable axis and the graphing axis.
An economic take on this is posted by Brad DeLong. Basically, Norway's revenues are not solely from corporate taxes, but from excise taxes on oil.Omitting these details misplaces them on this graph (and the curve cannot be charitably interpreted as anything other than a fraud).
http://delong.typepad.com/sdj/2007/07/caccianli-i-cie.html#comments
There's the more important question of whether the tax rate paid by corporations is anything other than zero.
Corporations don't pay tax because corporations don't really exist. To the extent corporations pass the tax on to stockholders, those stockholders are being taxed twice.
Anonymous, this is not true in most developed countries since shareholders are credited for the corporations tax paid. It was true in the US until Bush did away with the double-taxation of dividends.
This is pretty much the only aspect of Bush's tax cuts which you'll find are broadly suppotted by economists of all political bents.
Just a few comments on the "maximum / inflection point" issue:
On the Laffer Curve from Wikipedia, that is in fact a maximum, not an inflection point. For a differentiable function, a local maximum is at a point where the first derivative is zero. For a tax rate close to 0, the function has a positive derivative, and for a tax rate close to 100%, the function has a negative derivative. If the function has a continuous second derivative, then there must be a maximum somewhere between 0% and 100%. (Note the Martin Gardner Laffer curve that does _not_ have continous second derivatives.)
There is indeed no inflection point in the Laffer curve shown. An inflection point occurs when the second derivative is zero, and it may indicate a point where the concavity changes from up to down or vice-versa. As pointed out above, one way to test for a change in concavity is to see if a tangent line crosses the function.
A key point to bring out is the one implied in comments 22 and 24. The function is increasing and then decreasing, and hence the derivative is positive and then negative. However, the derivative is always decreasing, which is perhaps better stated as the second derivative is always negative. Since the second derivattive is always negative, there is not inflection point.
Sorry to be so long winded, but I taught calculus last year, and I went on and on about that stuff to my HS AP class. Everybody who knows math knows this stuff, but it can be tricky to people who haven't had to explain it to beginners recently. I'm sure that Mark CC just slipped when he said "inflection point" instead of "maximum".
It would be interesting to fit those data with a second or third degree polynomial. My guess from just eyeballing (sorry to be so technical...) is that the coefficients of the second and third order terms would be negligible. If one removed the U.A.E. point, the first order term would probably also be very small. So, it would seem there is very little correlation between the
tax rate (as stated in this plot) and the revenue (as % of GDP) collected. Does this imply that Laffer was simply wrong, or that the data are not what they purport to be (as mentioned by several posts above)?
Spudbeach, you don't need a continuous second derivative, or even first for that matter. So long as the function is continuous, it will have a max on the interval.
Anonymous:
Corporations pay takes because they *do* exist.
Incorporating a business is a tradeoff. By incorporating, the business becomes an independent legal entity, with a set of legal rights, like the right to own property, to
borrow money, etc. These rights are *independent* of the rights of the owners of the corporation; so if the corporation goes bankrupt, it forfeits *its* property, but not the property of the owners. The owners are shielded from risks by creating the corporate entity: they aren't liable for the corporation's debt, for legal liabilities of the corporations activities, etc. The assets of the corporation belong *to the corporation*; the profits of the corporation belong *to the corporation*. The corporation as an entity can decide to keep the profits within the corporation, or it can decide to pay them out to its owners. When it pays them to its owners, it is a *transfer* of assets from one entity to another.
In exchange for that separation of the corporation from the owners, making the corporation its own entity, the corporation becomes liable for taxes *as an independent entity*.
As a business owner, you *can* decide not to incorporate. If you do that, then your business isn't liable for any taxes on its own; the profits of the business belong to you, and you alone; and the only tax you'll pay on its profits are *your* taxes. But if the business fails, *you* are liable for its debts.
It's a tradeoff; you can separate the business assets and liabilities, making it a legal entity that needs to pay taxes; or you can take the risk yourself.
Seems perfectly fair to me.
To Bob O'H: I agree. Statistics are a very powerful tool when applied correctly, but as far as my (layman's) experience goes, but a tool that is particularly prone to misapplication and worse forms of abuse (e.g. just hinting at its application, as happened in this case).
Ceteris Paribus I guess. How else is an economist to earn a living?
As another professional statistician, I'd like to point out that this is not a case of bad curve fitting. I can't think of any way to fit a curve 'through' the data which results in what they've got, which is a curve which totally ignores all but two points in the left-hand portion of the data.
"Why would anyone believe that the Tax revenues were a function of a single variable?"
The Laffer curve is so fundamentally dishonest it shouldn't even be printed in plot form: the most one should ever be able to say is that tax revenue goes to zero at 0% and 100% taxation, and that implies that there must be a turning point somewhere in the middle. This is a complicated situation, though, and there may be more than one turning point. Furthermore, there isn't any good evidence of where those turning points should be, and it is almost certainly a dynamic function of societal conditions. Martin Gardiner's neo-Laffer curve on the Wikipedia page sums it up nicely.
I tend to look at anyone who actually prints a Laffer curve as a serious argument as being fundamentally dishonest, or incurably stupid.
"Why would anyone believe that the Tax revenues were a function of a single variable?"
Here's something else that ticks me off about the Laffer curve: I would strongly suspect that it is also dependent on the rate at which taxes are changed, and the direction . In a sense I would consider it a system which would probably exhibit hysteresis; if you lower taxes from some high value, you'll probably find a different 'peak' to tax revenue than if you raise taxes from some low value, if for no other reason than the psychological impact on investors and businesses.
I created a dataset based on the values in the chart, and ran a couple of regression equations to see what the data actually say. I thought it would confirm Mark's point, but there is a somewhat curvilinear relationship here. The bivariate correlation is .32, (p = .09), largely supporting Mark's linear interpretation. I then entered the squared term for tax rate to test the curvilinear relationship in the next step of the equation, and it had a beta weight of -1.16 (p = .11), suggesting that a quadratic curve (inverted U-shaped) also somewhat fits the data. With Norway excluded as an outlier, the linear relationship gets stronger (.41, p = .03), but so does the quadratic relationship (-1.27, p = .07).
Exclude the UAE (a special case because 0% tax forces 0% return regardless of all other factors), and exclude Norway too (just because that outlier looks suspicious and as though other factors might be in play -- and, yes, I know that's really dodgy reasoning!!), and what do you see? Pretty much a cloud of points, that simply suggests that the expected take from corporate taxation is about 3.5% of GDP regardless of the nominal rate. What does that suggest? This could occur if nominal rates of taxation are not actually well correlated with actual rates of taxation, due to the formulation of tax codes (with loopholes) and accounting practices.
Yup, the WSJ stuff is complete b*****ks (apologies to non-UKers who might not know what the *s stand for).
#54: "apologies to non-UKers who might not know what the *s stand for"
"Bricks"? "Books"? "Bjorks"? I'm TOTALLY lost! :)
Sam,
Your math reasoning may be dodgy but your conclusion is correct. Norway is an extreme statistical outlier on tax revenue. The mean tax revenue is 3.3%, with a standard deviation of 1.8. So Norway lies 3.7 standard deviations away from the mean-- an extreme outlier.
gg, nevermind the b0ll0cks
Isn't it slightly problematic that if you extrapolate their "fit" it actually goes negative before you reach the US/France corporate tax rates?
If WSJ wanted to be honest, the data for corporate income taxes paid as a percent of corporate income for the various countries are most likely available. They certainly realize that for most countries tax loopholes and surtaxes exist which skew the actual tax revenue from the stated tax rate. As Mark points out, this is simply a case of editorial dishonesty intended to suppport a prior bias.
Caledonian:
If you read the article, they clearly say that what they're talking about is that curve derived from that data.
When discussing the various tax burdens on corporations or individuals, I have not once seen any attempt to calculate a "total tax burden", or the percentage of one's income that one pays in taxes of all sorts. In this country there is a multitude of taxes from a wide variety of sources. There are not only federal taxes but state taxes, property taxes, school taxes, fuel taxes, sales taxes, inheritance taxes, service fees and the myriads of other ways various organs of government has to raise revenue. Focusing on one specific portion of tax at the exclusion of all others is deliberately misleading. Without knowing what the entire tax burden is on various corporations and how that differs depending on type of business, location and other circumstances, any analysis of the issue is going to be flawed from inception and more subject to the political biases of the people presenting the data.
Attempting to describe (or even postulate)a well-fit Laffer for an entire macro-economic world map is worthless and somewhat intentionally deceptive.
Caution: Laffer theory-work ahead--
It is easy to imagine how it might work for an individual actor: You have the opportunity to work overtime this week, or stay at home and watch football. Your decision will be based on the actual amount of money that you bring home, AFTER TAX.
So as the Gov raises your rate, your take-home on the overtime drops, and your marginal benefit becomes increasingly smaller.
At a certain point, it isn't worth it to you anymore, and you stay home.
When you give up the overtime altogether, the Gov loses ALL tax revenue on the overtime.
Ergo, by lowering the rate and putting more of the benefit of the extra work back in your pocket, the Gov encourages you to do the extra work. Lower rate, but more income to tax for the Gov. They "make it up on volume."
Of course, if they get the mix wrong, and lower it too much, you don't necessarily work more than you planned in the first place, so they are foregoing revenue needlessly. Find the "tipping point," as they say. The "point of diminishing return at the margin," as the economists would say.
Simple, right?
Well, not if you try to extend the theoretical construct from individual actors to the entire macroeconomic structure of the world!
Especially when the countries you "randomly" select to draw your bogus curve don't have the same (or in some cases even similar) tax structures or public policy goals, and are different in size, culture, climate, resource distribution and quantity, and type of government!
I mean seriously, what the heck were they thinking with this? It makes, like, no sense at all. Sigh. A little knowledge is a dangerous thing, I guess.
(But anyone with enough knowledge to get what they are saying or implying ought to see it for what it is...so who are they trying to BS?)
An easiler type of tax curve to graph:
Cato Policy Report, July/August 2007
The Global Flat Tax Revolution
By Daniel J. Mitchell
[Daniel J. Mitchell is a senior fellow at the Cato Institute and is currently writing a book on international tax competition.]
In the early 1990s, Rep. Dick Armey (RTX) proposed a flat tax. He would have junked the Internal Revenue Code and replaced it with a system designed to raise revenue in a much less destructive fashion. The core principles were to tax income at one low rate, to eliminate double taxation of saving and investment, and to wipe out the special preferences, credits, exemptions, deductions, and other loopholes that caused complexity, distortions, and corruption.
The flat tax never made it through Congress, but it's been adopted by more than a dozen other countries since 1994.
[truncated]
As seen in Table 1 {follow hotlink to see it; I'm unable to cut and paste it here as text}, most of the new flat tax nations are former Soviet republics or former Soviet bloc nations, perhaps because people who suffered under communism are less susceptible to class-warfare rhetoric about "taxing the rich."
[truncated]
Stipulated: The graph is stupid, and the Laffer curve is unemployable in anything but econ papers for academia.
I just think people are not quite clear on the corporate tax issue.
There is a really fine point to be made about the taxation of an entity that is essentially a conglomeration of shareholders. While, as Mark says, a corporation has some presence separate from its owners, there is more at play. The "legal" existence of a firm isn't quite the same as an extant taxable person. For instance, you can't put a firm in jail for accounting malfeasance. Taxes, fines, and profits all devolve to the people who own shares, including profits (if any) from the sale of assets once the operation of the firm is paid for. When tax is levied, it's levied on the activity the firm undertakes, and then on the transfer of profits (if any) to the shareholders. Increasing taxes means that either the shareholders make less, the firm gets rid of people/capital, or the company raises prices to compensate. The _elasticity_ of each is uncertain and highly variable. So not much may happen if taxes change some. If they change a lot, some combination of everything may occur. But it cannot be avoided that taxation of a corporation impacts not some independent legal entity only, but the people who constitute that entity's owners, workers, etc.
Also, while it's the kickbacks and backscratching loopholes that make the news, the biggest contributors to huge firms not paying taxes are the totally legal allowances for things like debt. The funny-biz comes from what firms group under the legal label as deductable. Items that are considered expenses help deduct from the amount that is taxed. But a lot of those expense are legitimate: there is no "loophole", there's just a distorted view on what should or shouldn't count towards expenses. Debt interest can be written off, for example, as is clearly expressed, no loophole required. But capital assets get financed through debt, and so on. The crying shame is the complexity of the tax code; to really figure out where companies hide things takes so much time and effort (and companies hire the people who would be good at finding it to actually DO it at much higher salaries), that we have a huge circular waste of time and money as people try to avoid taxes and the government hunts down illegal evasion. It's a tax that lots of firms avoid exceedingly well, and by doing so the firm deprives the government of revenue and the owners of value. So even if you really like having it, the country gets incredibly little from it.
Laffer curve is totally meaningless because it aggregates _present_ collections with potential collections in the _future_.
Besides, given that size of tax revenues represents nothing more than amount of resources expropriated from populace under threats of violence, the very idea that this amount should be maximized is quite dubious from a moral point of view.
For y'all that are wondering how that curve was derived, I'll tell you.
They didn't use excel to make that curve. They used powerpoint.
All this arguing about curve fitting seems to be giving them too much credit. As near as I can tell the y-axis is just a different form of tax rate. So they've graphed one tax rate, vs. a different tax rate. That's not even a laffer curve. The rest of the argument is moot.
The Laffer Curve itself only reflects a certain part of the economy - the part run by taxable corporations. If the state doesn't raise taxes from them at all (point 0/0), taxes would be paid only by individuals whose majority would work with corporations and thus receive higher wages (which would have the effect of a tax on revenues per employee), or cause a failure of the economy due to a decreasing demand of goods and services provided by these companies.
If taxation is at point 100/0, this means the entire economy is run by the state itself. No more corporations would be existent; a large amount of the tax sum would be necessary to invest and produce goods and services.
At any point in between, some profit stays with the private sector and will be spent, which creates demand, or saved, which creates demand later on (or devaluation or the next "financial crisis"). Some profit stays with the public sector and will be spent, which creates demand. - So, where's the difference that could cause any change in GDP?
I think huge differences between nominal and effective tax rates.