What Is Squeezing?

In the Physics Blogging Request Thread the other day, I got a comment so good I could've planted it myself, from Rachel who asks:

It’s a term I see used a lot but don’t really know what it means – what is a “squeezed state”? What does “squeezing” mean? (in a QM context of course…)

I love this, not only because it gives me an excuse to talk about cool physics, but because it will let me engage in blatant self-promotion-- I have a Science paper on squeezed states, which I've never actually written up for the blog. So this post will be a great way to set up a future post, ResearchBlogging that article...

We'll do this in the traditional Q&A format, though I hasten to add that the questions are not intended to represent Rachel in what follows (they sometimes get a little silly, so I don't want anyone to think I'm casting aspersions on Rachel).

You threw a Mr. Whipple picture up at the top of this post, like the gigantic Gen X dork that you are, but I'm going to assume that this doesn't actually have anything to do with toilet tissue? You're right, it doesn't. "Squeezing" in the context of quantum optics refers to a quantum process related to the Uncertainty Principle. With the proper manipulation of a quantum system, you can reduce the uncertainty in one of a pair of complementary, non-commuting observables at the cost of an increase in the other. I could've thrown a version of the Uncertainty Principle in there instead, but Mr. Whipple makes a better featured image than $latex \Delta E \Delta t \geq \hbar/2$.

I was with you up until "Uncertainty Principle," then... not so much. I assume you're going to explain this? Absolutely. Before we get to the quantum stuff, though, we need to back up and talk about classical physics. Specifically, the simple harmonic oscillator-- a mass bouncing at the end of a spring, say, or a pendulum swinging back and forth (provided it isn't swinging very far, anyway).

If you look at this sort of system, there are two properties of the system that matter: the position of the moving mass, and its momentum. If you track these two things as a function of time, you find that they oscillate back and forth, tracing out two sinusoidal curves that are out of phase with one another. When the position is as a maximum displacement from the center of the oscillation, the momentum is zero. Some time later, the position is at the center, and the momentum is at a maximum. Then the position is a maximum in the other direction, and the momentum is zero again. Then the position is at the center again, and the momentum is at its maximum value in the opposite direction. and finally, you come back to where you started.

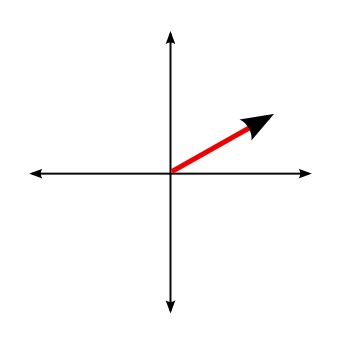
Now, you could make two graphs of these quantities, independent of one another, but in the 1800's, Henri Poincaré, among others, had a bright idea of a way to combine them into one plot. On the horizontal axis, you plot the position of the object, and along the vertical axis you plot its momentum. When you do that, the state of the system is uniquely represented by a single point somewhere in this "phase space." You can represent it by an arrow pointing to that spot, like this:

An arrow indicating the state of a system as a point in phase space.

The history lesson is nice, and all, but what does this have to do with squeezed states? I'll get there, don't worry.

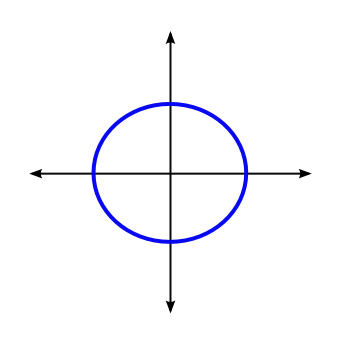
OK, I guess. So what's the point of doing this? Well, the beauty of this sort of scheme is that it lets you classify the motion of objects by looking at the shapes of their trajectories as they move through phase space. As time goes by, the point representing the state of our system will move around, and if we trace it out, we can see lots of interesting patterns. For a real system, these can get quite complicated, but for the simple harmonic oscillator, we just get a simple circle, like this:

A circular orbit in phase space.

That's a circle, all right. Again, why are we doing this? Well, this lets us know that we can reduce our system to a single, simple motion. Since the point representing our system is always on this circle, we only really need two numbers to characterize it: the radius of the circle (the "amplitude" of the oscillation), and the angle that an arrow pointing to the state at some instant makes with the horizontal axis (the "phase" of the oscillation). If we know the amplitude and the phase of an ideal harmonic oscillator, we know everything about it. We know where the arrow starts, and then it just spins around like the hand on a clock.

Which is nice if you want to talk about masses on springs, but I don't see what this has to do with quantum optics. Well, it turns out that masses on springs aren't the only harmonic oscillators out there. If you go through a bunch of math, it turns out that the equations describing an oscillating electromagnetic field can be written in a way that looks exactly like a harmonic oscillator.

So... light is a mass on a spring? In a mathematical sense, yes. If you make the proper choice of variables, you can describe an oscillating electromagnetic field with a phase-space plot just like the ones up above. You're not plotting "position" and "momentum," but with a bit of care you can define two quantities that have the same sort of relationship, and a graph of one versus the other makes a circle. The exact definition doesn't matter for our purposes-- just be aware that there are two "quadratures" of the field, and they're related in this simple way.

OK. I don't see what's getting squeezed, though. That's because we haven't talked about uncertainty yet. In a classical harmonic osicllator, you're allowed to specify both the position and the momentum absolutely perfectly. The state of the system is an infinitesimally small point at the tip of the arrow in the diagram above, specifying both position and momentum to arbitrary precision. That point can be located absolutely anyway, including exactly at the origin, which would correspond to a system with zero energy, just sitting perfectly at rest.

But that's classical physics. Quantum physics doesn't allow that, right? Exactly. In quantum mechanics, you can't specify both the position and the momentum arbitrarily well-- instead, each of them must have some uncertainty. Instead of an infinitesimal point at the origin, then, the lowest-energy state of the system is kind of a fuzzy blob centered on the origin, like this:

The lowest-energy state of a quantum harmonic oscillator, in phase space.

This is the Uncertainty Principle, right? Exactly. The product of the uncertainty in position and the uncertainty in momentum has to be greater than some minimum value, which means neither of them can be zero. That product can be thought of as defining an area in phase space, a fuzzy blob representing all the points where the tip of that arrow might be. For the lowest energy state of the system, that blob is centered on the origin, and we traditionally choose to define our units for the horizontal and vertical axes so that the resulting area is a circle. It's also the smallest that blob can possibly be, a "minimum uncertainty state" in the incredibly creative terminology favored by physicists.

So, that's for the harmonic oscillator. And the same thing is true of a light field? Right, because you can make the math look exactly the same. For the right choice of units and parameters, the phase-space plot of a quantum light field containing, on average, no light at all, looks like a fuzzy blob centered at the origin, with the minimum possible uncertainty.

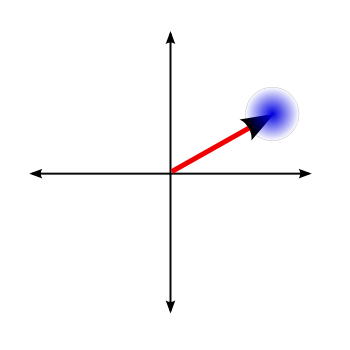
Oooookay. But no light at all isn't interesting. How do you describe some actual, you know, light? Well, it turns out that the best you can do, in terms of coming close to the classical picture, is to just move that blob out to some distance away from the origin. You still have a minimum uncertainty state, but it sits at the end of an arrow corresponding to some particular amplitude, like this:

A coherent state, the minimum uncertainty state of a quantum optical light field.

So, what does that mean? Well, the way to think about it is to imagine that the tip of that arrow lies at some indeterminate position within that blob. You can still associate some amplitude with the field-- because the arrow has a length-- but there's also an uncertainty in that amplitude. You can also assign it a phase, from the angle with the horizontal axis, but there's uncertainty in that, as well.

And this is still a minimum uncertainty state? Exactly. The circle is the same size as the one that was at the origin, just moved out a bit. If you let the amplitude become very large, so the arrow is much longer than the radius of the uncertainty blob, this becomes an excellent approximation of a classical light field. A fairly bright laser produces a field that's basically exactly what you expect from classical radiation, described beautifully by this kind of picture.

The technical term for this is a "coherent state," and the mathematical description of these is (part of) what won Roy Glauber a share of a Nobel Prize.

Are we going to get to the squeezing part soon? Yep; right now, in fact.

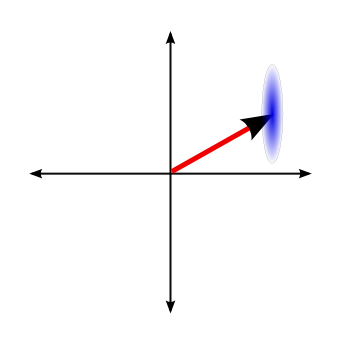
These coherent states describe a particular arrangement of uncertainties that corresponds to something very close to a classical field. They're not the only possible minimum uncertainty states, though. You can deform that uncertainty blob if you like, and create states that aren't circular blobs, provided you keep the total area the same. Like this:

A squeezed state, in phase space.

In this graph, we've reduced the uncertainty in one quadrature of the field, while increasing it in the other. The area of the resulting elliptical blob is supposed to be the same (though I did this freehand, so it probably isn't), with the increase in one exactly matching the decrease in the other. this looks kind of like--

Kind of like you took the original blob and squeezed it. Is that the origin of the name? Exactly. Which is relatively creative, for physicists.

So, does this thing still clock around the original circular path? More or less, yes. This is a "quadrature squeezed" field, with the reduction and extension happening in directions corresponding to the two perpendicular axes of our phase-space plot.

The fact that you're defining this particular arrangement suggests there are other ways to do this. Well, yeah. You can also have "amplitude squeezed" states, where the uncertainty in the length of the arrow goes down, and "phase squeezed" states, where the uncertainty in the angle of the arrow goes down. In either case, the uncertainty in the perpendicular direction goes up.

If that first thing clocks around at the same orientation, wouldn't that get you both of these? Right. If you have a quadrature-squeezed field like in the graph, and the arrow is along the horizontal axis, that's the same as amplitude squeezing. And if the arrow is along the vertical axis, that's phase squeezing.

So, this is something you can actually do? How? The usual techniques with light involve things like non-linear materials whose optical properties depend on the intensity of the light. If you have the higher-amplitude parts of your light field changing at a different rate than the low-intensity parts of your light field, that tends to stretch the blob in phase space. And there's a mathematical rule showing that you don't usually increase the area of these blobs-- I want to say that's Liouville's theorem, but I could be misremembering-- so as long as you start with a minimum uncertainty state, like a laser field, you end up with a squeezed state.

That's all very nice, but one thing's bugging me. When you talk about quantum light, you usually talk about photons. But you haven't mentioned the particle nature of light at all. What gives? Well, I'm trying to start simple. But yes, you're absolutely right, when you do this all out, you need to go to a description of light in terms of photons.

In terms of these phase-space plots, you can think of the number of photons associated with the field as describing the length of the arrow. This means that the arrows can only take on certain allowed lengths, each corresponding to a circle of a particular radius, which means a particular number of photons. So there's a length for, say, 100 photons, and a slightly longer arrow for 101 photons, but you'll never see an arrow of a length between those two values.

But... What does that mean for our uncertainty blobs? It means that they're composed of lots of different photon numbers, each with some probability. So, you have some probability for finding 100 photons, and another probability for 101, and 99, and so on. This is peaked at the value corresponding to the center of the blob, and drops off as you go higher or lower.

Technically, the minimum uncertainty condition ends up corresponding to a Poissonian distribution of photon numbers, which is a distribution whose width is simply related to the average number (it's the square root, in fact, but that doesn't really matter). An amplitude-squeezed state has a distribution that drops off more quickly than the Poisson distribution as you move away from the average ("sub-Poissonian"), and a phase-squeezed state has a distribution that drops off more slowly ("super-Poissonian").

But, wait, if the length of the arrows tells you the number of photons, doesn't that mean photon states are perfect circles? With a particular radius, yes. These are called "Fock states" if you're not tired of vocabulary yet.

But... How do you add together a bunch of circles to get a little blob? Very, very carefully.

Sorry to be flippant, but that's really a nasty, complicated issue. Constructing a sensible description of the phase of a quantum system is really tricky, and there are people who will argue that there is no such thing as an absolute optical phase of a single quantum system.

I've never entirely understood either side of this particular argument, so let's just leave it as "It's complicated," and move on. Please?

Fine. But what's all this good for? Well, when you start thinking about making measurements in quantum optical systems, these uncertainties produce noise in your signal, and limit what you can do. If you try to build, say, an interferometer, like LIGO, your sensitivity to changes in position is limited by the width of those uncertainty blobs.

But the critical thing is that it's limited by the width of those blobs in a particular direction. If you're clever about what you're measuring, you can use squeezed states to make better measurements, by decreasing the uncertainty in the direction you care about, at the cost of increasing the uncertainty in the other direction, that you don't care about.

Because of that, there's a lot of interest in squeezed states for precision measurement. Most of this involves light, but back at the turn of the millennium, I was involved in a project trying to do this with atoms, for possible use in an atom interferometer.

Which would be that Science paper you mentioned earlier? Exactly. which I will wwrite up another time, because this is long enough as it is.

Yes, yes it is. I hope this answers the basic question of what a squeezed state is and why it's called that, though. If not, well, you know where the comments are...