I've spent a bunch of time recently blogging about baseball statistics, which you might be inclined to write off as some quirk of a sports-obsessed scientist. I was very amused, therefore, to see Inside Higher Ed and ZapperZ writing about a new AIP report on women in physics (PDF) that uses essentially the same sort of rudimentary statistical analysis to address an important question.
I say "amused" because of the coincidence in methods, not because of the content. And, in fact, the content is... not likely to make them friends in a certain quarter of the blogosphere. I actually flinched when I read the sentence "This is further evidence that there is no systematic bias against hiring women." That phrasing is incredibly unfortunate in that it is likely to be interpreted in ways that will really upset some people.
It is, however, a true statement given their analysis and the relatively narrow question they're trying to answer. And it's an important enough point that it's worth writing up in a little more detail than IHE or ZapperZ did, to make clear what they are and are not saying. I'm not going to do this is funny Q&A format, though-- writing about this at all is somewhat fraught, and trying to crack wise while writing about this study is basically guaranteed to blow up in my face, so I will keep this as matter-of-fact as I can.
The new study is a statistical analysis of the distribution of women in physics, attempting to address the question of all-male departments. The statistics are pretty striking, and summarized in this table that I cribbed from Inside Higher Ed (hopefully the formatting won't go all wacky due to differences in CSS):
Physics Departments, Faculty Size and Gender
| Highest physics degree awarded | Bachelor's | Ph.D. |
| Smallest department (# of faculty members) | 1 | 3 |
| Median size of department (# of faculty members) | 4 | 22 |
| Largest department (# of faculty members) | 27 | 75 |
| Women's representation on physics faculty | 16% | 11% |
| Departments that have no women | 47% | 8% |
| Departments that have no men | 1% | 0% |
| Number of departments | 503 | 192 |
Those data seem pretty damning at the bachelor's-only level: nearly half of all physics departments have no women at all. Surely, this is evidence of bias, right? Those all-male departments must be a result of old-boy networks of sexists who won't hire women.
What the study shows, however, is that this can't actually be taken as evidence of bias, because many of these departments are very small-- the median size of a department at a bachelor's-only institution is four professors (meaning, for the record, that Union, where I work, is way above average-- we have eight tenure lines and two (soon to be three) permanent but non-tenured lecturer positions). Given that, there's actually a pretty decent chance of ending up with an all-male department just from basic statistics.
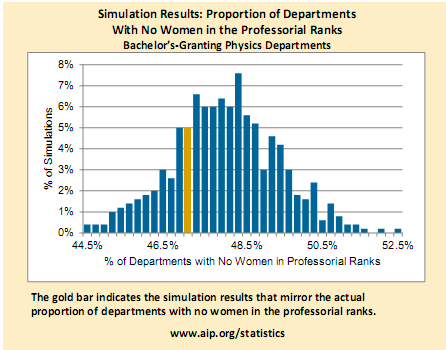
They demonstrate this by basically the same method I used in the first of the baseball posts linked above: they set up a simulation where they take an imaginary population of faculty with the same gender ratio as in the real sample, and assign them to departments of the same sizes found in the real sample completely at random. This is a little more complicated than the simple toy model I used for the baseball thing, because the probability of getting each gender changes as they assign faculty to departments. Then they look at what fraction of the imaginary departments ended up being all male. They repeated this 500 times, and got the graph showing how many of their 500 simulations gave a particular percentage of all-male departments that's the featured image up top, which I'll repeat here:
What you see is something that looks pretty much like a classic "bell curve" distribution, showing that there's an average fraction of departments with no women, and some uncertainty about that average. The yellow bar indicates what they see in the actual sample, which you can see is slightly below the peak of the distribution (the most likely value is 49%, they see 47%), though within one standard deviation of it. The same graph for Ph.D.-granting institutions looks like this:
Again, you see an average with some uncertainty, but the yellow bar is a little harder to see, because it's way off in the left wing. The observed number of all-male departments is much smaller than you would expect from a random distribution-- the most likely value is 12%, and the real sample is 8%. In fact, 90% of their simulations gave higher all-male fractions (so the real value is a bit less than two standard deviations below the mean). The overall numbers are all much lower, reflecting the larger average size of departments at Ph.D. granting institutions-- given a larger number of faculty, the odds of a random draw ending up all-male are much lower.
This suggests that if there's any systematic preference happening in hiring, it goes in the opposite direction of the most basic sort of sexism-- women are, in fact, somewhat more broadly distributed among departments than you would expect from simple chance. The fact that a sizable fraction of physics departments do not have any women is not by itself an indicator of bias against women, given the fraction of the faculty pool who are women. If you wanted to insist on putting a negative spin on this, you could try to argue that it's indicative of some sort of tokenism-- a willingness to hire one woman so the department isn't entirely male, but not more than one. But that doesn't seem all that likely, and if anything goes a bit against the conventional wisdom about women on hiring committees and so on.
Now, there's a big and important caveat to this, which is the emphasized clause in the previous paragraph. They have assumed a particular gender distribution among the imaginary faculty pool in their simulation, which matches the gender distribution of the real sample-- 16% of the bachelor's-only faculty are female and 11% of the Ph.D.-granting pool. That's descriptive, not prescriptive-- they would undoubtedly prefer a more equal split (and in fact re-run their simulations for higher fractions of women), but they're looking at what's actually out there for the purposes of this analysis. And it's important to remember that those low percentages are over all ranks of faculty-- from newly hired assistant professors to the moldiest of why-won't-he-retire-dammit full professors-- and thus include the effects of decades of past hiring decisions.
(They do, for what it's worth, give one quick indication of the present state, in their Figure 5, which shows that the percentage of women increases as you move to younger cohorts. The Assistant Professor (that is, pre-tenure) ranks are over 20% female, a percentage that's slightly higher than the fraction of women receiving Ph.D.'s in recent years. This is where you'll find the sentence quoted above that made me flinch-- "This is further evidence that there is no systematic bias against hiring women." Which is, as I said, a somewhat unfortunate phrasing, but not an inaccurate summation of their data: women are hired into tenure-track faculty positions in the same proportion that they graduate with Ph.D.'s, so looking at the system as a whole from the 30,000-foot-altitude kind of level, there's no clear indication of bias-- if anything, there's a very slight preference for hiring women. Though they note that even with a higher fraction of women in the pool, you would still expect some number of single-sex departments-- they ran simulations with numbers matching the assistant professor distribution (where, again, the proportion of women is slightly higher than among recent Ph.D. graduates), and those would give 37% single-sex departments at the bachelor's level and 3% at the Ph.D. level. Even at a 50-50 split among faculty, you'd end up with around 10% of bachelor's-only departments having no women (though in that case you'd also get 10% with no men...).)
What are the limitations of this? Well, it's a very global, 30,000-foot-altitude kind of study. All they can really say is that, on the basis of statistics, it is unlikely that there is a global, systematic bias against women that leads to the large number of all-male departments. The fact that a department has no women, particularly at a smaller school, does not necessarily indicate any bias in hiring beyond whatever may be indicated by the gender distribution of the available faculty pool.
This does not mean that there is absolutely no sexism anywhere, and that's not what they claim. All they can and do say is that the distribution we see in reality is no worse than you would expect from a purely random distribution. This does not rule out the possibility of bias in any individual department, or even some large number of biased departments, provided they are balanced by some number of unbiased or oppositely biased departments.
This also doesn't say anything about what kinds of jobs people have, or what they're paid, or any of a host of other kinds of potential bias. You could undoubtedly construct a pathological sort of system whereby the global appearance of no bias was produced by systematically excluding women from a small number of highly prestigious positions while distributing them more evenly among a larger number of low-status jobs. This kind of analysis will not allow you to detect that sort of problem (though there are other ways to get at those kinds of questions, and I have no doubt that AIP and other organizations are doing those tests).
This is basically analogous to the situation in the second of those baseball posts linked at the beginning. The batting average data I was playing around with are broadly consistent with what you would expect for a single, constant "innate" average-- that doesn't mean that you can't have an innate average that changes with time, just that you can't point to anything in the statistics that unambiguously shows those sorts of changes. Similarly, these data are broadly consistent with an unbiased (in a statistical sense) random distribution of women among faculty jobs, and that doesn't mean bias doesn't exist, just that there's nothing in the statistics that unambiguously indicates the presence of bias.
(Now, there are other arguments you could raise about this, like whether we ought to expect or want the hiring of candidates for faculty positions to resemble a random distribution. You could also argue that there ought to be a much stronger preference given to women in order to equalize the overall distribution, but that's a flamewar of a different color. And, obviously, a much more equal distribution in the candidate pool (more that 20% women) would be a wonderful thing, though that's an issue with an earlier part of the pipeline than they're considering here. Again, this study is descriptive, not prescriptive.)


I know that a handful of (mostly small, bachelors-only) colleges are still single sex. Most of these are women's colleges, but there are a handful that are still all-male. And some of these, such as Wellesley and (at least 20 years ago; I haven't checked if they have gone co-ed recently) Rose-Hulman, almost certainly would have physics departments. I would expect single sex institutions to prefer hiring professors of the same gender as the student body, but I don't know if that's actually true. I also don't know if there are enough single-sex institutions with physics departments to make a big difference.
I'd expect there might be a few departments that skew toward a male faculty for various reasons. The service academies come to mind. Their departments are large, and the effective size would depend on whether you included uniformed faculty as well as civilian, but there might be enough numbers to cancel out the small liberal arts women's colleges in the bachelor's column.
I don't really know much about the number of single-sex institutions out there-- in the sector of higher education I'm used to thinking about, the number is small, but I'm often reminded that there's a whole tier of religiously affiliated colleges and the like that just never make it into my awareness. I don't think their numbers would be big enough to skew anything, but I doubt it. It's possible that single-sex institutions trying to match the gender of their students is the source of the 1% of bachelor's-only institutions with no male faculty (that only needs to be about 5 schools, after all), but I doubt there are enough all-male colleges to significantly move the fraction of all-male faculties.
I only skimmed it, but I didn't see anything about the applicant pool. They use 11% and 16% as the percentages of female faculty that current processes hire into two different categories of institutions, and then assume them randomly.
If the applicant pools at PhD-granting and BA-only institutions are 11% and 16% female respectively, then they have a good case that the cause of disparities is not bias in the hiring process but rather problems in the processes that produce the applicant pools. However, I didn't notice any reference to the composition of the applicant pools.
I think this kind of statistical work points out an interesting point. When we do statistics-based evidence testing, we're doing it against a default hypothesis which we then falsify. But what hypothesis should we be taking as the default?
The results here aren't "the null hypothesis is correct", but rather "there's no reason to reject the null hypothesis (that the selection is unbiased)". I'm going to guess that a bunch of the grumbling on these results will boil down to the complaint that the null hypothesis they used (no bias), while possibly useful from a computational standpoint, is not really the default hypothesis that should be up for falsification. The (possibly implicit) argument will be that due to a long and well attested history of bias, the default hypothesis (or the Bayesian prior, if that's what you're into) should be one of bias, and it is incumbent on those who wish to prove unbiasedness to falsify the default hypothesis of bias, rather than simply show that the no bias hypothesis can't be excluded.
Alex: I only skimmed it, but I didn’t see anything about the applicant pool.
The only information about the applicant pool is mentioned in passing, around Figure 5. They show the gender distributions for different faculty ranks, and note that the fraction of female assistant professors is slightly higher than the fraction of Ph.D.'s awarded to women in recent years (the most recent report I could find from AIP used the 2008 class, and produced this graph, showing the fraction of Ph.D.'s to women at a bit less than 20%). There's a bit of an inference involved in calling that a statement about the applicant pool, but I don't think it's too much of a stretch to say that the assistant professor ranks are mostly filled with relatively recent Ph.D.'s. And even if they go back further than that, the number of Ph.D.'s earned by women has been steadily increasing, so a wider time window for the applicant pool would most likely lower the fraction of women in the pool.
It's also worth noting that the pattern of recent hires having a slightly higher fraction of women than recent Ph.D.'s goes back several years-- the same thing shows up in this report on 2006 data, so that's not a total fluke.
RM: The (possibly implicit) argument will be that due to a long and well attested history of bias, the default hypothesis (or the Bayesian prior, if that’s what you’re into) should be one of bias, and it is incumbent on those who wish to prove unbiasedness to falsify the default hypothesis of bias, rather than simply show that the no bias hypothesis can’t be excluded.
That's certainly an argument you could make, but if you're going to do that, you would need to have a clear criterion for falsification, and I'm not sure how you'd do that. To show a lack of bias, would you need to show that no single department engaged in biased hiring? Over what span of time?
Maybe a better way to think about this might be to view it as a limiting measurement. (I'm probably only saying this because of my long-standing fascination with precision measurement searches for new physics...) That is, this result does not rule out the existence of bias in hiring, it just places a particular limit on the size and scope of the possible effects. A more sensitive measurement-- something that looked at prestige and salary as well, or did a more direct comparison to the candidate pools for new hires-- might well find something, but the basically random distributions they see here suggest that the effects can't be all that big on a global scale. This might rule out the minimally supersymmetric grand unified theory of gender bias, as it were, but there are lots and lots of other versions that are still viable, and only weakly constrained by these data.
I'm not an expert in statistics, but I think "the default hypothesis of bias" mentioned by RM needs to be quantified, e.g., "the default hypothesis of bias larger than X" or "the default hypothesis of bias within Y of X"; then you have to choose X (or X and Y). Probably the only reasonable way to do so, lacking a solid theoretical basis, is by looking at data, in other words, by emperically estimating the bias; the AIP report suggests (subject to the caveats and assumptions discussed by Dr. Orzel) that, if you do so, the error bars for your choice of X will include 0, and empirically falsifying the non-null hypothesis will be difficult or impossible (for a suitable statistical interpretation of the word "impossible"), even if it is false.
It's not that the null hypothesis is computationally useful; it's genuinely useful. A very real problem with choosing a default non-null hypothesis is that, if it is falsified, somebody might hypothesize a different (smaller) non-null hypothesis, and if that is falsified, another, and so on; vast sums of money have been diverted from productive research to falsify a seemingly endless stream of unjustifiable non-null hypotheses (I'll refer you to the Respectful Insolence blog). The key word here is "unjustifiable", which is what the null hypothesis is useful for.
Why do simulations when you could get an exact expectation value from the Poisson distribution formula?
David,
The departments were not all the same size.
They do, in fact, invoke the Poisson distribution, and use it in assigning imaginary faculty to imaginary departments. The problem is, they're dealing with a wide range of different sizes of departments, which makes it very difficult to get a single prediction. You might be able to generate something, but the calculation would be so tortured nobody would be able to follow it, and the simulation is easier and more convincing in that case.
For the record, I think there the generally accepted number of remaining "independent" (meaning they aren't intimately connected with an all-female college, and only separate in name only) all-male schools in the US is 3: Moorehouse College in Atlanta (which has some partner schools but still retains a significant independent identity), Wabash College in Illinois, and Hampden-Syndey College in Virginia (which had a female valedictorian a few years ago, but only because faculty children of any gender are allowed). This does not include vocational religious schools of course.
All three currently have male-only physics faculty, according to their websites. Make what you will of this information.
Crap, that contained some typos. Notably Wabash is in Indiana not Illinois (stupid memory).
Wow, the way the author of this post and of the AIP paper contort their language with so many conditionals, warnings, disclaimers, caveats, and limitations before getting to the point.