This topic is an addition to the original list in the introductory post for the series, because I had thought I could deal with it in one of the other entries. Really, though, it deserves its own installment because of its important role in the history of laser cooling. Laser cooling would not be as important as it is now were it not for the fact that cooling below the "Doppler limit" in optical molasses is not only possible, but easy to arrange. That's thanks to the "Sisyphus cooling" mechanism, the explanation of which was the main reason Claude Cohen-Tannoudji got his share of the 1997 Nobel Prize in Physics.
So, you're finally going to explain those colder-than expected temperatures? Yep.
Took you long enough. Well, it's a complicated subject. It requires four pieces to work, three of which we've talked about at least briefly: one is that when you put multiple lasers together to make optical molasses, you can get patterns in the intensity and polarization of light, that are useful for making optical lattices, thanks to the second piece, the light shift changing the energy levels of the atoms. The third piece, mentioned briefly at the end of the lattice post, is that the atoms in question have multiple sub-levels, which can experience different light shifts.
The final bit is a phenomenon called "optical pumping."
Does this involve moving atoms through light pipes? No, "light pipes" are a completely different thing. Optical pumping is a way of moving a population of atoms between their internal states. By using the right kind of light, you can arrange to put nearly all of the atoms in a sample into a particular internal level of your choice.
The key to this is that light carries angular momentum that depends on its polarization. If the light has right-hand circular polarization, an atom absorbing the light not only acquires the energy of the photon, moving one electron to a higher energy state, it also increases the angular momentum of that electron by one unit. If the light has left-hand circular polarization, the angular momentum of the electron decreases by one unit. This moves an electron from one of the ground-state sublevels to a different sublevel in the excited state.
So you optically pump atoms into higher angular momentum excited states. But they don't stay in the excited state, so how does that help anything? They don't stay in the excited state, true, but when they drop back down to the ground state, they can only change their angular momentum by at most one unit-- they can go down one, up one, or stay the same.
This fact lets you move electrons into the maximum angular momentum state very quickly, through the absorption and emission of several photons. That's the "pumping" of optical pumping-- you use light to move all the atoms into one of the extreme states.
I don't follow. If the decay is random, how can you pump atoms in a particular direction? It helps to look at a cartoon of a simple example system. The simplest atom with multiple sublevels has two ground-state levels, and four in the excited state (these are labeled with half-integer values, for reasons that don't matter for our purposes):
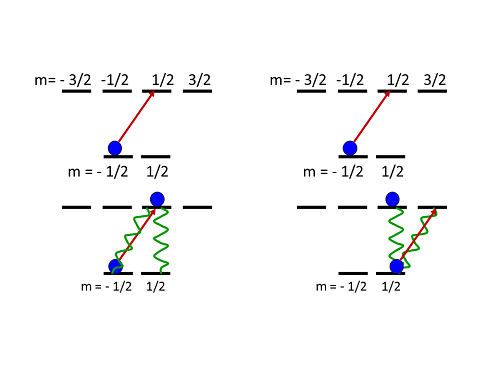Cartoon of optical pumping. Right-hand circular polarized light drives atoms into higher angular momentum states.
If you start with an atom in the negative angular momentum state and shine in right-hand circular light, you get the situation on the left: the atom absorbs a photon, and moves up in angular momentum as it goes to the excited state. From there, it can decay back to where it started (decreasing by one unit) or to the other of the two ground-state levels (dropping straight down, with no change of angular momentum). There's no higher-angular-momentum state for it to decay to, so it can't increase its angular momentum during the decay. If it goes back to where it started, it repeats the process, getting excited back up to the higher angular momentum state again.
If it decays to the other ground-state level, though, it's stuck. It can absorb a photon and go to the higher angular momentum excited level, but from there it can only go back to one ground-state sublevel. There's no state for it to decay to without decreasing its angular momentum.
This means that an atom starting in the negative-angular-momentum sublevel of the ground state will inevitably end up in the positive-angular-momentum sublevel when exposed to right-hand circular polarized light. It might take several cycles of absorption and emission, but those happen very rapidly-- tens of nanoseconds-- so in a fraction of a millisecond you can move essentially all the atoms in a sample into the positive-angular-momentum state.
And if you use left-hand circular polarization, it goes the other way? Exactly. Left-hand light will inevitably drive the atoms into the negative-angular-momentum ground-state level. Either direction will work, depending on your choice of laser polarization.
And this gets you cooling... how? These states have the same energy, don't they? So what's the difference? They start out with the same energy, but remember, they're in a laser field where the polarization of the light changes as you move from one place to another. And that means the two levels are subject to a different light shift, depending on the polarization of the light.
Why is that? In a very loose way, you can think about it in terms of the optical pumping process. An atom in the negative-angular-momentum state sitting in right-hand circular light isn't going to stay in that state very long, so it doesn't interact with the light all that much, and feels a small light shift. Once it's in the positive-angular-momentum state, though, it stays there and interacts strongly with the light, feeling a big shift.
The opposite is true for left-hand circular polarization: in left-hand circular light, the negative-angular-momentum level feels a big shift, and the positive-angular-momentum state feels very little shift. And this is the key to Sisyphus cooling.
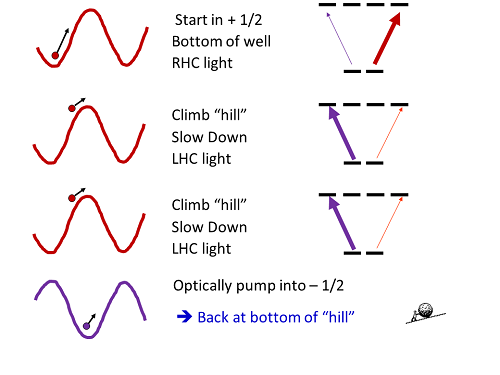
How does that work? Well, here's a cartoon of the process, drawn from my lecture slides for this stuff:
Sisyphus cooling.
Imagine you start in a region of right-hand circular polarization, with an atom in the positive-angular-momentum state. It feels a big light shift, lowering its energy. As it moves, though, it starts to leave the area of right-hand circular polarization, and the light shift decreases, so its internal energy goes up. That energy has to come from somewhere, so it slows down, as if it were rolling up a hill.
When it gets to the top of the "hill," then, it's lost some amount of energy (the exact amount depends on the intensity and detuning of the lasers). But the whole reason it's at the top of the hill is that the polarization of the light field has changed-- now it's not sitting in right-hand circular light, it's sitting in left-hand circular light. And a positive-angular-momentum atom doesn't last long in left-hand-circular light before it gets optically pumped to the negative-angular-momentum state.
Which puts it back in a place with a big light shift? Exactly. When it pumps to the negative-angular-momentum state, that state is light shifted down. Which means it's back at the "bottom" of the hill, but now it's moving slower than it was initially.
Doesn't it get back the energy that it lost? No, because it's carried off by the light-- the photon it emits in going from the excited state to the negative-angular-momentum ground state has a very slightly higher energy that exactly makes up the change in the light shift. So it lost energy climbing the hill, and then finds itself back at the bottom.
Thus, "sisyphus cooling." Exactly. The atom's predicament is exactly like the punishment meted out to Sisyphus in the afterlife, after he pissed the Greek gods off in some manner I don't recall-- he was condemned to push a giant rock up a hill, but every time he neared the top, the rock would slip away and roll back to the bottom, forcing him to start over.
It didn't pay to piss the Greek gods off. No, they had a sick sense of humor. It works out well for atomic physics, though, because this effect turns out to be an exceptionally efficient way of cooling the atoms down. You get Doppler cooling at the start, and once the atoms are fairly cold, enough that the light shift is roughly the same scale as their kinetic energy, the sisyphus effect becomes important, and cools the atoms down to temperatures well below what you expect from the simple theory.
And nobody expected any of this? I can't say I'm surprised, given the complexity... It's not quite true to say that none of this was expected-- people knew about optical pumping, and in fact, that's how they justified using the simple two-level theory for talking about laser cooling. They reasoned that the light would pump all of the atoms into the extreme angular momentum states in very short order, and once that happened, you really had only two levels to worry about, so the simple theory should be just fine.
What they didn't anticipate was the effect of the polarization gradients. But once they started using optical molasses beams with different polarizations, the gradients happen automatically, and you get sisyphus cooling. And thus, much lower temperatures than had been believed possible.
Pretty cool, if you'll pardon the inadvertent pun. Just one question, though: Why were they using optical molasses beams with different polarizations? Isn't that more work? Well, there were two reasons: one was to avoid making an intensity pattern-- if you use the same polarization for beams in opposite directions, you end up making a standing wave with spots where there's no light at all. Using different polarizations lets you make a uniform intensity field, and that's nicer to think about.
But there's another, technological, reason why you would use beams with different polarizations, but...
I know, I know, that's the next post in the series... Got it in one.
- Log in to post comments