I realize people are getting sick of reading me talk about this charged-tape business, which has run to one, two, three, four posts at this point. Truth be told, I'm losing enthusiasm for it myself. So this will be the final post, at least for now...
As I mentioned on Twitter, as I type this stuff up for the blog, I've toyed with the idea of hanging onto it instead, and writing it up for The American Journal of Physics or The Physics Teacher, so I could get a little professional credit for it. There are two problems with that (other than that some stick-in-the-mud editor or reviewer might regard these posts as prior publication: one, that I don't have time, and two, that I can never quite wrap everything up.
The last thing that occurred to me as something to do with this and my toy model of the system was to validate the atomic physics measurement I did with this, by simulating the behavior of charged tape interacting with an uncharged tape. This is a pretty straightforward modification of the VPython code I had (I decided not to be hard core and calculate the field at the uncharged object, and use that to get a polarization, and then a force, but just stuck in the equation for the polarization force). This works very nicely, and behaves just like you would expect:
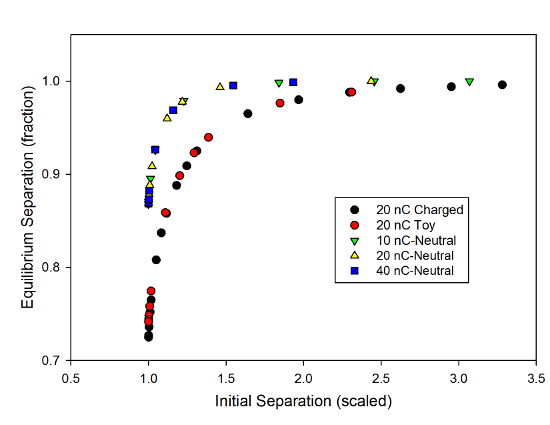 Simulated results for charged tapes, using the toy model to simulate the force between a charged tape and an uncharged but polarizable one.
Simulated results for charged tapes, using the toy model to simulate the force between a charged tape and an uncharged but polarizable one.
There are two curves in this, one showing the scaled results of the pendulum and toy models for the case with both tapes charged, and the other showing the scaled results for the charged-neutral toy model. Both of these show universal tipping point behavior, but the charged-neutral system "tips" much more rapidly, and settles at a smaller equilibrium distance.
That's exactly what you expect for this system, given the mathematical expressions for the forces. With both objects charged, the force drops off as the square of the separation-- doubling the separation decreases the force by a factor of 4-- while the charged-neutral case drops off as the fifth power-- doubling the separation decreases the force by a factor of 32. That means you need to get much closer to see a significant attraction, but also makes the "tipping point" behavior sharper, because the room for error is smaller.
Given these results, then, I decided to check what I did in that atomic physics post, and see if I could extract the polarization I put into the code by comparing the tipping points. Using the same procedure as that earlier post, I got a value of $latex 1.4 \times 10^{-17} $ for the polarizability. The problem is, the number in the code is $latex 3 \times 10^{-18} $, a factor of 4.5 smaller.
So, I thought maybe the problem is that I need to compare the equilibrium positions, not the initial separation. That's a slightly different calculation, which I won't grind through here, but when I do it out, I get $latex 1.25 \times 10^{-19} $, a factor of 20 too small.
So there's something wrong here, either with my code, or the analysis of getting a polarizability out of this method. And chasing that down is going to be fiddly and annoying. But the polarizability thing is probably the coolest aspect of this whole business, so I would need to understand that if I were going to write this up for a more formal outlet. Thus, this will probably stay on the blog.
Then again, we're short of projects for summer students, as two of our most research-active faculty are on sabbatical and not taking any students, so maybe I could put somebody on this and make it their job to figure out what idiotic error I made in setting up the code for the simulation...

One thing I would like to know is why does the tape pick up charges when peeled of? What relevant physics is at work here?
I suspect it's chemistry, actually. Something to do with the electron affinities of the molecules in the adhesive, etc.. I know that the best results come with the "invisible" tape that's sort of translucent-- the clear stuff doesn't work well at all. It also depends on the surface you're pulling it off of-- when we do this in lab, we have students put down a "base" tape and put everything else on top of that, so we know what we're dealing with. There's some variability in what happens to that base tape when you pull it up, that may depend on whether it's on a wood lab table or the formica counter.