The Sound of Simulated Bombs

So, last week I idly wondered about the canonical falling-bomb whistle. The was originally intended to be a very short post just asking the question, but I got caught up in thinking about it, and it ended up being more substantial. And leaving room for further investigation in the form of, you guessed it, VPython simulations.

This one isn't terribly visual, so you don't get screen shots, just a link to the code at Gist. It's a simulation of a falling bomb, with air resistance, tracking the velocity as a function of time. Then it calculates a "Doppler shift" using the velocity as a fraction of the speed of sound for an observer standing on the point of impact, and another some distance away.

Putting this together required some guesstimated numbers, so I gave the bomb a mass of 1000kg, a radius of 30cm (which don't seem wildly unrealistic from this page about WWII munitions) and dropped it from a height of 6000 m (around 20,000 ft, which is a reasonable value for high-altitude WWII bombing; I'm using WWII as a reference point because the whistling-bomb noise dates back at least that far).

What I wanted to see was how significant the shift would be for somewhat realistic conditions, and whether this could make a sound like the canonical falling-bomb whistle, decreasing in pitch. Looking at the physics, as in the diagram above, it ought to-- the falling bomb starts out coming toward the observer, shifting up in pitch, but an observer off to the side should see the velocity become more tangential as it drops, eventually coming back to whatever the default whistle frequency is. The question I wasn't sure about is how significant this change in pitch could be.

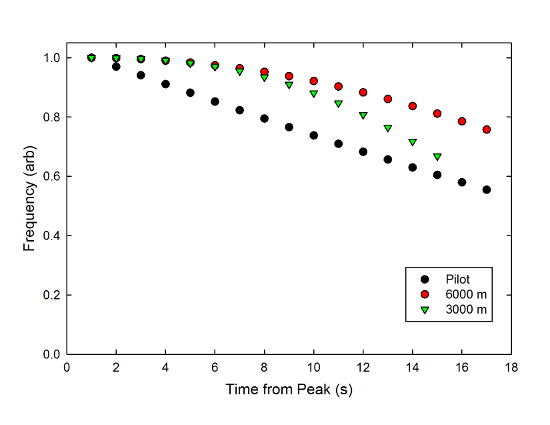
So, what does the simulation show? Well, the primary output is this graph:

Doppler shift due to a 1000kg falling bomb with a 30cm radius.

There are three curves here. The black points show the shift as seen by an unlucky person at the impact point, and it increases through the whole fall. In the absence of air resistance, this would be a straight line, but with air resistance, there's a little bit of curvature. The red points are for an observer who starts out 6000m away (the same distance as the height the bomb drops from), and first increases in pitch, then decreases. The green points are for an observer 3000m away from the impact point, and the shift is more dramatic, because the bomb has a velocity toward them for longer than in the more distant case.

The shift here is fairly substantial, because the bomb is falling very fast. It also does exactly the sort of thing you expect from looking at the velocity components above: first goes up, then down. So, you could get a falling-bomb whistle with the canonical decreasing pitch provided you're standing off to the side of the impact point. The closer you get to the impact point, the more dramatic the shift, both in terms of amplitude and speed-- if you make the distance to the observer just 600m, the shift goes from 70% above the original pitch to zero in just six seconds (not plotted here).

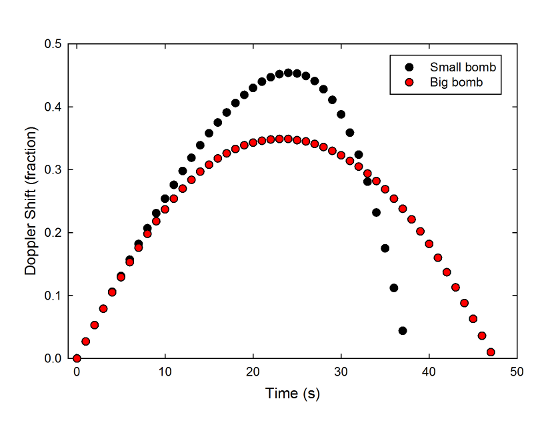
Now, this obviously presumes a particular size and shape, and thus an effect of air resistance. So, if we change the size, what happens? I tried doubling the radius for the same mass, and you can see what that does here:

The Doppler shift of a falling bomb for two different sizes, showing the effect of air resistance.

A bigger radius means more air resistance, and thus a slower terminal speed (this almost reaches terminal speed), which in turn means that it takes longer to hit, and has a smaller peak shift. You still get the reversal in pitch, though.

The other question that came to mind back when I was thinking about this was whether the decreasing-pitch whistle was a result of imagining things from the perspective of the person dropping the bombs rather than the person being bombed. I've seen clips of bombs being dropped where they seem to whistle as they leave the plane, but that might've been a dubbed-in effect, for all I know.

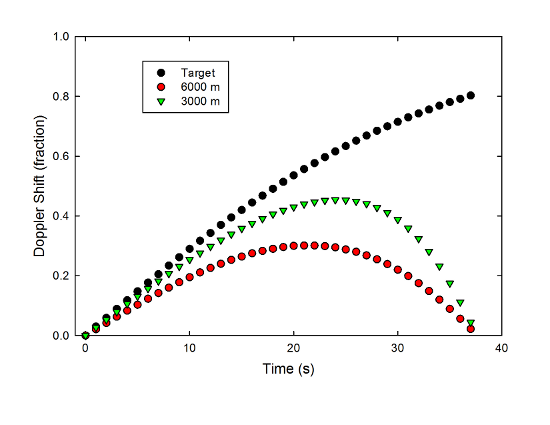
Anyway, just for fun, I thought it would be interesting to compare the decreasing-pitch whistle of bombs observed from a safe distance to that of a bomb dropped directly from a plane, which led to this graph:

Doppler shift of a falling bomb during the decreasing-pitch phase compared to the shift heard by the person who dropped it.

The Doppler shift just depends on the velocity, which is initially increasing at a steady rate due to the acceleration of gravity, so we expect the points for the pilot's perspective to fall on a straight line, and they do. The others are decidedly non-linear, but again, we expect that, because it should go like the cosine of the angle to the line of sight.

So, does this accurately reproduce the falling-bomb whistle? I had hoped to make Mathematica reproduce the sound pattern here, but it's very picky about which users it's friends with, and life is just too short to keep wrestling with that program. We can turn to some eyewitness testimony, though, in the form of a comment that must have a good story behind it, left by Time Eisele:

I can vouch for the ‘descending whistle’ sound in the case of falling bowling balls, at least. From an estimated peak altitude of about 1500 feet, and standing approximately 1000 feet away from the ultimate impact point, the sequence goes:

- Whistle starts by getting gradually louder at a more or less constant pitch.

- In the last few seconds of the drop, the pitch drops noticeably, all the way down to the ground.

And, you know, that looks pretty much like what we see in this graph: a slow decrease from the peak at first, that rapidly speeds up toward the end of the drop. So, I think this works out nicely. I'd like to know why Tim was being bombarded with bowling balls, though...