One of the points I make repeatedly in teaching introductory mechanics (as I'm doing this term) is that absolutely every problem students encounter can, in principle, be solved using just Newton's Laws or, in the terminology used by Matter and Interactions, the Momentum Principle. You don't strictly need any of the other stuff we talk about, like energy or angular momentum.
Of course, just because you can solve any problem using the Momentum Principle doesn't mean that you want to solve those problems that way. As an example of a problem that's really annoying to solve with just the Momentum Principle, I generally break out a toy looping roller coaster that we have in the department's collection of demo gear. And, sinc eI have a slow-motion camera now, I shot some video of it:
That's three clips spliced together, partly because the camera's format doesn't play nice with Tracker Video (sigh...), but mostly because it makes a useful point, namely that if you don't start the car high enough up the track, the car won't make it all the way around the loop.
It's easy enough to calculate the speed the car needs to have at the top to make it around using just the Momentum Principle, but finding the position on the hill where it will reach the necessary speed at the top of the loop is a harder matter. You can get a good estimate of the start position very quickly if you think about the problem using energy methods, though-- at the top of the loop, the cart has to have a minimum speed, and it's above the ground by some amount, so you can work out the total kinetic plus potential energy it has as it makes the loop. all of that had to come from the gravitational potential it has at the top of the hill, which lets you get the start height. And, indeed, that's how I figured out where to have my student hold the cart for the second and third clips in the video...
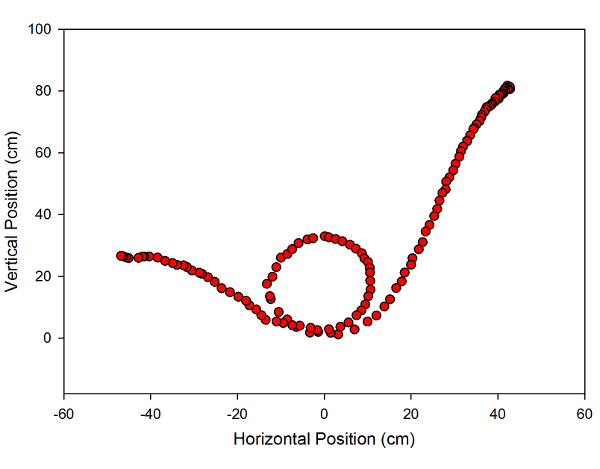
Since I have this, of course, I can crank the clip into Tracker Video Analysis (once the idiot format problem is fixed, sigh...) and measure the position of the car as a function of time. Which gets me a reconstruction of the track that looks like this:
Reconstruction of the roller coaster track from positions measured in Tracker Video.
(Yeah, it's a little oblong, but I was selecting these positions using a trackpoint on a laptop, so I wouldn't read too much into that...) Those positions let you work out the velocity of the car as it goes, which can be combined to find the speed:
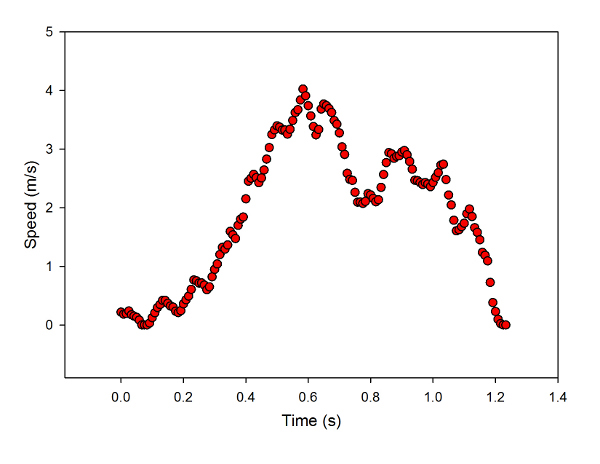Speed of the car going around the loop, as a function of time. Smoothed by taking a running average of five points.
This shows basically what you expect: the speed increases to a maximum at the bottom of the hill, drops as the cart climbs the loop, reaching a minimum at the top, then goes back up on the way down. The reconstruction of the loop shows a radius of about 15cm, which implies a minimum speed to complete the loop of around 1.2 m/s. The minimum seen in the speed graph is a bit over 2 m/s, a nice safety margin.
Since Rhett is already done for the semester (I have two more weeks of class, grumble mutter grump), I guess it falls on me to assign you some physics homework, so:
-- The graphs above are for the first of the video clips. Do your own video analysis of the second and third clips, and find the minimum height for the release.
-- Use the difference between the peaks in the speed graph to estimate the force of friction and air resistance acting on the car as it rolls along the track.
-- Use the reconstruction of the roller coaster loop to write a VPython simulation of the car moving on the track using only the Momentum Principle.
Send your homework to Rhett for grading, since he has lots of free time these days.
- Log in to post comments
If you add friction, its hard for me to imagine solving it without resorting to forces to derive a PDE (plus a constraint to stay on the track). Then energy isn't conserved anymore. So in reality, for many realworld problems we get stuck with complexity.
@Omega Centauri #1: You're quite right in principle, but in practice the coefficient of rolling friction is quite small (few e-3 or less), so for a lab demo, where the mass (and therefore normal force N) is small, neglecting friction is entirely reasonable.
If you were tasked to build a comparable _full-size_ looping track, say for a Nissan television commercial, then you would certainly have to take the car's rolling friction into account. Of course, then you'd turn to some proper physics numerical software, rather than trying to do the engineering by hand.
I'm still trying to figure out if it is necessary for the object to stay in contact with the track.
zebra: I think it could come off the track, as long as the trajectory takes it back into contact. And of course its orientation must not depart too much, or else it won't land on the wheels.
Analysis is much easier if you impose the constraint however, then you really only then have two degrees of freedom, position along the track, and velocity along the track. Of course integrating a 2DOF PDE is almost childsplay given modern computers, just throw it into your favorite PDE integrator.
When the car just barely makes it around, it does come slightly off the track. You can't see it very well in the video, but in real time you can hear it.
There very definitely is energy lost to friction, which you can see from the homework question about the second peak-- the first time it passes the bottom of the hill, it's going at about 4 m/s, but after the loop it's barely 3 m/s. The estimate of the start position is pretty good, though, and it's a useful lower limit in a half-page of algebra. That's usually enough to get students to buy into the idea, at least.
Omega C, if you are still there,
In the idealized case, with no losses, and using a point object instead of the truck*, I don't think it can lose contact with the track. The wording got me thinking about it because this problem is always presented as "making it all the way around", but really that means "without bouncing".
*You can see the rear wheels detach but not clear what the front ones are doing--too complicated.
zebra: In the idealized case with a point object and no friction, there must still be a range of starting positions where the object can come to a stop relative to the track at a point where the track is "above" it, and then fall straight down. This obviously applies at least for the starting position that brings the object to a stop at the exact top center of the loop, and I think also for a stop on the upper left quarter of the loop (in the orientation shown in the video). It might not be possible after the object passes top center, but only because it can't come to a stop afterward.
Zack, thanks for your reply.
Yes, although the object, if it detaches from the track in that second quadrant, (9 to 12 o'clock) is not going to fall straight down, since it has a horizontal component of velocity.
I think the point of the exercise is to determine what the velocity entering the loop has to be to get to that 12 o'clock position; that's why I was confused by Chad's language. Once you get there, contact will be maintained in the third quadrant.
@zebra: The minimum speed Chad quotes in the post is actually the minimum speed the cart has to have at the top of the loop. Neglecting friction, the forces in the problem are gravity and the normal force applied by the track. The vector sum of these accelerations must equal the instantaneous acceleration of the cart. To simplify things, I will assume the loop is a circle (this cannot be exactly true, but should be close enough) and consider only the top of the loop, where the change of speed is zero. At this point gravity plus normal force must equal the centripetal acceleration, which is v^2 / r. But both of these forces point downward, so if the required centripetal force is less than that of gravity, the cart will fall off the track. Therefore, the speed at this point must be at least sqrt(r*g), which, using r = 0.15 m and g = 9.8 m/s^2, gives v_min of about 1.2 m/s.
Eric Lund,
I'm well aware of the standard explanation; it happens that Chad got me thinking about the problem differently-- just my quirky way of interpreting the words, I guess.
Let's say that an object enters the loop at the top, with some horizontal velocity v. (Supported until it is exactly at the vertical diameter.)
Clearly, for some v, the object will stay within the circle but not in contact. There is a minimum v for which it will stay in contact.
Can you determine what that v is, without invoking the standard centripetal acceleration argument?
There is probably some Lagrangian technique to solve the problem, and you may be able to do it without explicitly invoking the centripetal acceleration argument, but I suspect it will still be lurking in your equations.
"Stay within the circle but not in contact" is generally a bad outcome for this kind of experiment. Unless the rate of angular rotation is exactly right, your next contact with the circle is unlikely to be with the wheels. You also seem to be thinking of a circle as a 2-D object, but there are some applications, and this is one, where it is more useful to think of it as a 1-D object. The coordinate of interest is position along the track (angular position along the circle, if you can make that approximation), and you want position in the other two dimensions to be irrelevant.
Eric Lund,
Lagrangian? Lurking equations? Jeez, I posed the question for anyone at the physics 101 level as Chad described his class-- using the equations of motion with gravity and not energy. And maybe some pre-calc/calculus.
Any takers out there? Omega C?
This is one of those fox terrier cases where everyone knows "this is how you do that problem" but has trouble with articulating what is going on.
Zack@7:
A point object does not do what you describe except if it was going much slower and stopped at the left edge of the loop and then fell straight down (for an instant). What it does in the situation you seem to be describing is what you see happen in the third demo. It leaves the track and follows a parabola rather than a circle. I assume analysis of that case is the second tracker video HW assignment.
zebra@12:
Eric is just telling you that the alternatives to a solution that uses Newton's Laws in an inertial frame for the circular motion plus energy (to get you there) are quite messy and usually involve a lot more math. Indeed, energy conservation is just a way around having to do a lot of math with Newton's Laws and a non-constant acceleration.
#13 CCPhysicist,
Clearly, this is the "word problem" problem, which Chad has discussed in the past. At the physics 101 level, a bright student could answer my question (#10) with only perhaps looking up one formula from pre-calculus. I don't see how that is "quite messy" or "a lot more math".
But what's required is being able to visualize and conceptualize and verbalize what is happening. I don't know if Chad checks back on these threads but I would be interested to know if he also sees this as an example of that issue.
I think it's certainly an example of the phenomenon where you can state a relatively simple problem in mechanics in a way that makes it present as confusing to more experienced physicists in more or less the same way that simple problems present as confusing to students in the intro courses. We occasionally have this problem with our "Help Center" tutors, upperclass students who work to assist intro students with homework, etc. Every now and then, particularly in the term when we offer intermediate mechanics, one of them will start writing down Lagrangians to solve a first-year physics homework problem, and then we have to talk the intro class back down...
I don't immediately see an easy solution to the question in #10, given the no-centripetal-force constraint, but then, I'm a little groggy this morning for no immediately obvious reason.
Chad,
I appreciate the response.
Actually, I think it is exactly the same issue for both the beginning student and the expert-- thinking: "I should know this.", which leads to either despair or the hammer approach. That's why I am in complete agreement with the sentiments you expressed a while ago about your brilliant daughter's experience with the more cognitive and exploratory approach to math.
I think the problem can be solved if you draw a picture of various paths that the object might follow, with and without the 12-to-3 o'clock quadrant of the track in place. You only need to know the standard equation for projectile motion. Now, I may be mistaken about what gets covered in pre-calc or analytic geometry these days, but then there's the internet, which will provide the other necessary formula to enable calculating the solution.
I'm going to assume that people followed through on my hints and didn't find any errors in the approach I suggested-- otherwise I would be getting roundly chastised!
Anyway, I would argue that this is a more fundamental and intuitively sound way of looking at the problem WRT conservation of momentum.