Less Than Absolute Zero

I'm sitting in a hotel in Utah at the PQE 2013 conference.  As I write this, the temperature is a rather brisk 19F. (For everyone else in the world, -7.2C) That's not cold at all to some of you, but some of you didn't grow up in south Louisiana.

Once a year they let us grad students out of the basement!

Either way, on the Kelvin scale the weather here is still a balmy 267 degrees above absolute zero.

Which is as cold as it gets, right? Right. As a result, I've seen a lot of hubbub online about a new result published in the journal Science: Negative Absolute Temperature for Motional Degrees of Freedom. The coverage in the popular press has not actually been that bad, explaining that negative temperature in this context is really quite hot in the casual sense of the word. The issue is simply that formally temperature is a relationship between energy and entropy, and you can do some weird things to entropy and energy and get the formal definition of temperature to come out negative. I've seen a few good popular explanations of this on forums and such, but I want to see if I can get the gist across in a slightly different way that doesn't require us to keep explicit track of entropy (which tends to be really complicated).

The simplest model of at atom, at least to us AMO physicists, is called the two-level atom. It pretends that an atom is a system that can be in one of two states depending on how much energy its electrons have. If the electrons are just orbiting in their lowest orbit, this lowest-energy state is called the ground state. If some external source of energy such as a beam of laser light or a collision with another atom knocks the electrons into a higher orbit, this higher-energy state is called the excited state. These are the only two possible internal states of the atom. Simple as this model is, it works surprisingly well in many real-world applications.

I mentioned that one of the ways a two-level atom can be bumped into its high-energy state is by collisions with other atoms. If a ground-state atom gets hit hard enough, it'll become an excited-state atom. If an excited state atom gets hit, its electrons de-excite, fall back to the ground state, and transfer the excited state energy either to the electrons of the other atom or just to the overall recoil speeds of the atoms after the collision.

At low temperature, most atoms are in the ground state. They move around slowly, and mostly don't hit each other hard enough to bump them into the excited state. At higher temperatures, they hit each other harder and the excitation happens more often. As the temperature goes up, so does the fraction of the atoms in the excited state. But as the population of excited state atoms gets higher, they get hit and de-excited more often. Here's a graph of the fraction of atoms in the ground and excited states (for hydrogen treated in a two-level approximation) as a function of temperature in Kelvin. Top curve is ground state, bottom curve is excited state:

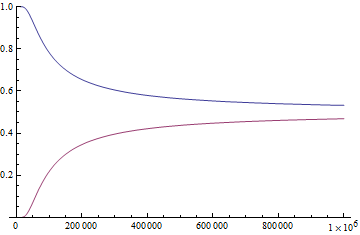Two things stick out. First, at normal human-scale temperatures of ~300K, pretty much everything is in the ground state. But no matter how much heat we pump into the system, no matter how much we crank up the temperature, we can never get any more than 50% of atoms in the excited state. The reason is the de-excitation; excited state atoms that get hit aren't excited anymore, but cranking up the hit rate is the only way to get ground state atoms excited in the first place. It's diminishing returns.

On to the math. One of the major results in statistical mechanics is the fact that the fraction of atoms in a given energy state Ei is given by:

$latex p(i) = \frac{e^{-E_i/{kT}}}{\sum_n e^{-E_n/{kT}}} &s=2$

(Where k is Boltzmann's constant. Here there are only two levels, so the sum on the bottom only has two terms.) Crank T way up and each exponential goes to 1, giving a probability closing in on 1/2 for an atom to be in either state. But always, always, the lower energy state will have more population.

Unless I cheat by not limiting myself to temperature as a method for exciting the atoms. What if I start with a huge pile of ground-state atoms, and one by one I whack them with a hammer to get them excited and then throw my collection of excited atoms into a jar. Well, they'll start hitting and de-exciting each other, but before that process finishes I sure enough have more excited state atoms than ground state atoms. Is there any way to represent that fact with the equation above? There sure is - let T be a negative number. Sure, I didn't get there through just dumping heat into the system. But given that I did in fact get to that population inversion, it formally acts like a negative temperature system in that it has more excited atoms than are possible with any finite positive temperature. Negative temperatures are thus in essence really really hot. Let me re-plot the same graph, with negative T included:

The two curves have traded places on the left side of the graph.

Now this kind of thing isn't new. An ordinary laser contains a population inversion and is in this same sense a negative-temperature device. It's not at thermal equilibrium though, and if you stick a thermometer in your laser's gain medium it will register a quite ordinary positive temperature.

The achievement of the authors of this Science paper is that they have managed to obtain this kind of negative-temperature in the motion of the atoms themselves, not just the internal degrees of freedom of the atoms. This is a clever and interesting result. But don't worry - in the usual "average energy of the atoms at thermal equilibrium" sense, absolute zero remains the coldest possible temperature.

UPDATE: Just before hitting post, I see that Chad's just posted on this as well. Go read it!