How often does the sun emit 1 TeV photons?

I had an interesting question posed to me recently: how frequently does the sun emit photons with an energy greater than 1 TeV?

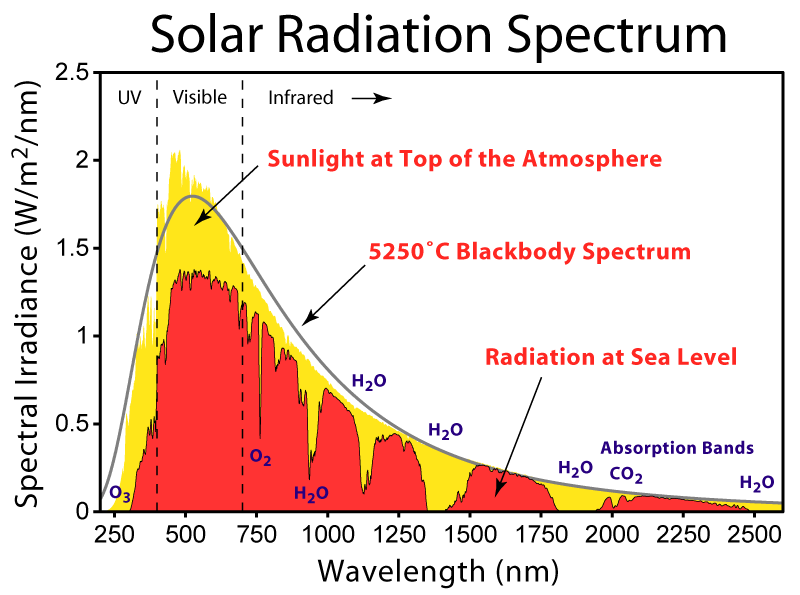
All of you know about the experiments going on at the LHC, where particles are accelerated to an energy which is equivalent to an electron being accelerated through a potential difference of trillions of volts (which is what a "trillion electron volts" - a TeV is). During the ensuing collisions between particles, high-energy TeV photons are produced. Of course everything is emitting light in the form of blackbody radiation all the time. Human beings emit mostly long-wavelength infrared, hot stoves emit shorter-wavelength infrared and red light, hotter objects like the sun emit across a broad range of wavelengths which include the entire visible spectrum. Here, from Wikipedia, is the spectrum of the sun:

Solar spectrum.

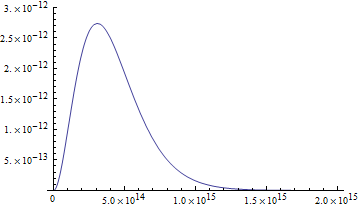
This graph is given in terms of wavelength. For light, energy corresponds to frequency, and frequency is inversely proportional to wavelength. Longer wavelength, lower frequency. A TeV is a gigantic amount of energy, which corresponds to a gigantically high frequency and thus a wavelength that would be pegged way the heck off the left end of this chart pegged almost but not quite exactly at 0 on the x axis. Let me reproduce the same blackbody as the Wikipedia diagram, but cast in terms of frequency:

Same spectrum, in terms of frequency

Here the x-axis is in hertz, and the y-axis is spectral irradiance in terms of watts per square meter per hertz. (That makes a difference - it's not just the Wikipedia graph with the x-axis relabeled although it gives the same watts-per-square-meter value when integrated over the same bandwidth region.)

Ok, so what's the frequency of a 1 TeV photon? Well, photon energy is given by E = hf, where h is Planck's constant and f is the frequency. Plugging in, a 1 TeV photon has an frequency of about 2.4 x 10²⁶ Hz. That's way off the right end of the graph. Thus you might think the answer is zero - the sun never emits such high-energy photons. But then again that tail never quite reaches zero, and there's a lot of TeVs per watt, and there's a lot of square meters on the sun...

So to find out more exactly, let's take a look at the actual equation which gave us that chart: Planck's law for blackbody radiation:

$latex \displaystyle B(f) = \frac{ 2 h f^3}{c^2} \frac{1}{e^\frac{h f}{kT} - 1}&s=2$

So you'd integrate that from 2.4 x 10²⁶ Hz to infinity if you wanted to find how many watts per square meter the sun emits at those huge frequencies. (Here k is Boltzmann's constant, which is effectively the scale factor that converts from temperature to energy.) That's kind of an ugly integral though, but we can simplify it. That $latex e^\frac{h f}{kT}$ term? It's indescribably big. The hf term is 1 TeV, and the kT is about 0.45 eV (which is a "typical" photon energy emitted by the sun), so the exponential is on the order of e^{2200000000000}. (The number of particles in the observable universe is maybe 10⁸⁰ or so, for comparison.) Subtracting 1 from that gigantic number is absolutely meaningless, so we can drop it and end up with:

$latex \displaystyle B(f) = \frac{ 2 h f^3}{c^2} e^{-\frac{h f}{kT}}&s=2$

which means the answer in watts per square meter is

$latex \displaystyle I = \int_{a}^{\infty}\frac{ 2 h f^3}{c^2} e^{-\frac{h f}{kT}} \, df&s=2$

where "a" is the 1  TeV lower cutoff (in Hz). That exponential term now has a negative sign, so it's on the order of e^{-2200000000000}. I'd say this is a safe place to stop and say "The answer is zero, the sun has never and will never emit photons of that energy through blackbody processes." But let's press on just to be safe.

That expression above can be integrated pretty straightforwardly. I let Mathematica do it for me:

$latex \displaystyle I = e^{-\frac{a h}{k T}}\frac{2 k T (a^3 h^3+3 a^2 h^2 k T+6 a h k^2 T^2+6 k^3 T^3 )}{c^2 h^3}&s=2$

So that's an exponential term multiplying a bunch of stuff.  That bunch of stuff is a big number, because "a" is a big number and h is a tiny number in the denominator. I plug in the numbers and get that the stuff term is about 10⁹³ watts per square meter, and you have to multiply that by the 10¹⁸ or so square meters on the surface of the sun. That's a very big number, but it's not even in the same sport as that e^{-2200000000000} term. Multiplying those terms together doesn't even dent the  e^{-2200000000000} term. It's still zero for all practical purposes

Which is a lot of work to say that our initial intuition was correct. 1 TeV from blackbody processes in the sun? Forget it.

Now blackbody processes aren't the only things going on in the sun. I don't think there are too many TeV scale processes of other types, but stars can be weird things sometimes. I'd be curious to know if astrophysicists would know of other processes which might bump the TeV rate to something higher.

[Personal note: I've been absent on ScienceBlogs since April, I think. Why? Writing my dissertation, defending, and summer interning. The upshot of all that is those things are done and I'm now Dr. Springer, and I have a potentially permanent position lined up next year. And now I might even have time to write some more!]