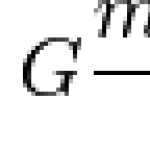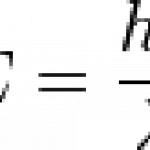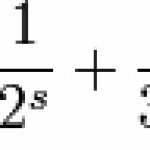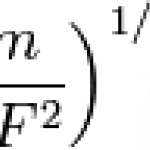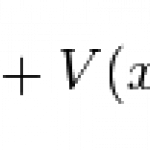mspringer | April 20, 2011Last time, we did some slightly boring groundwork. This time, we're going to look at something more interesting: the way a pulse of light propagates in something (like a piece of glass) with a frequency-dependent refractive index. As we discussed, the refractive index is just a way to express the phase velocity of a monochromatic continuous wave. If a medium has a refractive index of 1.5, then the speed at which the crests and troughs of a continuous wave travel is c/1.5, where c is the speed of light.
But here's the interesting part - there's really no such thing as a purely continuous…
mspringer | April 13, 2011So we left off with the most basic mathematical description of a wave. It's a function of the form f(x - vt), or in words a disturbance that moves from one place to another at a constant speed without changing shape.
This is a nice start, but it's both too general and not general enough to be useful. To general because f can be any function at all, and few mathematical techniques can conveniently handle anything you throw at it. Not general enough because waves can and do change shape, move at varying velocities, and so forth. We need to do better.
"Better", to a physicist looking at waves,…
mspringer | April 7, 2011So, what's a wave? In his deservedly ubiquitous undergrad electrodynamics textbook, David Griffiths emphasizes the fact that the whole idea is pretty nebulous. Any rigid definition is likely to exclude things that are usually thought of as waves or to include things that aren't. He suggests that one possible vague definition is "a disturbance of a continuous medium that propagates with a fixed shape at a constant velocity". He goes on:
Immediate I must add qualifiers: In the presence of absorption, the wave will diminish in size as it moves; if the medium is dispersive different frequencies…
mspringer | March 14, 2011A while back I was driving in my car listening to the radio and was gobsmacked to hear a song (What's My Name? by Rihanna and Drake) in which the singer's rap involved accurately estimating a square root. Unfortunately it was in the context of a rather vulgar play on words ("the square root of sixty-nine is eight-something..."), and in fact the local station is now censoring everything after "square root". But still, mathematics on the pop charts! Who'd have guessed?
So today's function is the square root function, familiar to adults and school children alike:
As the kids are told by their…
mspringer | March 12, 2011So there's this alien invasion flick called Battle: Los Angeles. It's getting mixed reviews. Ebert hates it - "an insult to the words "science" and "fiction," and the hyphen in between them." With the caveats that his judgment is usually questionable, I haven't seen the movie, and I don't plan to see the movie, I'm thinking I'm relatively safe in trusting his opinion in this particular case.
Now it's also true that judging this kind of movie by its physics is an exercise in foolishness, akin to complaining about the lack of 8 consecutive 24 episodes of Jack Bauer enjoying a good night's sleep…
mspringer | March 11, 2011In the last post I talked about a measurement we did in our lab to characterize some properties of two parallel laser beams. The theory, if you want to dignify that equation with such a title, gave the power of the two beams as a function of mow much of the beams we cut off with a moving opaque block at position x.
The equation had 6 constants - the power of each beam, the width of each beam, the separation of the beams, and background power with no beams. Compare this to Newton's law of gravitation:
For two masses m1 and m2 separated by a distance r, this equation gives you the force. If…
mspringer | March 4, 2011A while back in the lab we were conducting an experiment that involved passing a laser beam through a narrow iris, using a beamsplitter to take half the intensity of the beam and send it one way, with the remaining half passing through undisturbed. Then we arranged our mirrors in such a way as to bring the beams together so they were propagating in the same direction parallel to one another before doing some jazz that will hopefully make an interesting journal article.
To get a good handle on calibration, we wanted to characterize the two parallel beams. Laser beams, despite how they might…
mspringer | February 27, 2011Here is a picture of the earth, with latitude and longitude lines in ten-degree increments:
Despite the fact that each vaguely rectangular area formed by the intersection of those lines forms a 10 degree by 10 degree region, the actual square-mile area of each rectangle varies. The ones near the poles are smaller than the ones near the equator. It turns out that the area of a little square patch of land with sides given by some fixed interval of latitude and longitude will be proportional to cos(φ), where φ is the latitude. (NB: for those who're used to seeing sin(φ) in their spherical area…
mspringer | January 25, 2011I always tell my students that they should never just write down an equation blindly and start plugging things in. If you don't understand what you're doing, you're much more likely to make a mistake.
Sometimes I don't take my own advice. On a science forum I read occasionally, a person who was just taking their first quantum mechanics class asked just how exactly you would go about preparing a system such as a hydrogen atom in a particular quantum state. It was correctly suggested that at room temperature, pretty much all of the atoms would automatically be in the ground state by virtue of…
mspringer | January 22, 2011In my free time during data acquisition runs and the like, I've been paging through Hardy and Wright's famous textbook An Introduction to the Theory of Numbers. It has something of a legendary reputation among pure math textbooks, and so far as I can tell it is entirely deserved.
One of the topics treated in the book is the representation of numbers in the decimal system. In some ways it's an elementary topic, but it also serves as a starting point for some genuinely deep mathematics. Today I'd like to noodle around with the connection between fractions and decimals. It's a bit of a stretch…
mspringer | January 17, 2011This Christmas I got a little handheld GPS, which I've been using mostly for geocaching. As the device acquires signals from the various satellites dutifully orbiting overhead, it displays your position coordinates and a figure indicating the estimated uncertainty. At the beginning of the acquisition or if the view of the sky is poor, it might be something like 50 feet. If you have a clear view of the sky and are receiving signals from many satellites, it might be as low as 11 or 12 feet.*
This figure is called the circular error probable. In essence, there is a 50% probability that your GPS-…
mspringer | January 14, 2011Well, last time we were looking about the classical probability density for a bouncing ball, and the quantum mechanical probability distribution for the same. They looked not even a little bit alike. This is kind of a problem, since we know from experience that classical physics works pretty well, and from more modern work we know quantum mechanics works pretty well also.
However, despite their apparent inconsistency it turns out that we're just not looking close enough. The quantum nature of things is usually (though not quite always) apparent when the energy level of the system in question…
mspringer | December 16, 2010All right, I'm gonna delay the next installment of the quantum bouncing ball for a brief diversion. I have a friend who's also a physics grad student, and he suggested that we along with a few other fellow students form a yet-to-be-named unofficial club whose raison d'etre is to get together every few weeks and do interesting Mythbusters-style science for no good scientific reason. After all, we are fortunate enough to be surrounded by expensive cutting edge equipment and brilliant people, and we should have some scientifically interesting fun.
One suggestion for something we might try was…
mspringer | December 13, 2010Right now I'm on the 4th floor of the physics building. If I walk down the hall to the balcony overlooking the atrium, I could drop a bouncy ball and watch its trajectory. It'll fall to the ground, bounce up to some fraction of its initial height, and repeat the process with a loss of energy each time until it finally comes to rest. In a perfect world with no dissipation of energy, the ball would always bounce exactly up to its initial height and repeat its trajectory forever.
In principle, I can drop the magic ball at a given time on the stopwatch and thenceforth predict exactly where it…
mspringer | December 3, 2010
Isaac Newton, when he wasn't revolutionizing mathematics and almost single-handedly inventing physics as a systematic discipline, wrote some really ridiculous stuff. Alchemy, occult esoterica, you name it. In his defense, it was the 1600s. He didn't have a whole lot of prior scientific understanding to help him sort the wheat from the chaff.
Until he reached the age at which the position is traditionally handed to a successor, Stephen Hawking occupied Isaac Newton's chair at Cambridge University. I don't know what his excuse is.
Stephen Hawking's book The Grand Design should be read by all…
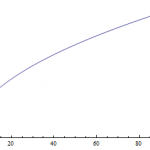
mspringer | November 21, 2010In pure mathematics there's not too many function studied more than the Riemann zeta function. For reasons of historical tradition, the generic variable name that's usually used is s instead of z. (The function is mostly interesting in terms of complex analysis, so x would be a bit unorthodox too.) It's defined in the following way:
On the real line, it looks like this:
Not terribly exciting, most of the interesting action happens for complex values of s. The reason that the action is interesting is that the zeta function is intimately connected to the prime numbers, despite there being no…
mspringer | November 13, 2010Shortly after the invention of the laser, a torrent of discoveries began pouring in thanks to the previously unreachable intensities that became available. Many of these discoveries fall under the general category of "nonlinear optics", which you could more or less say is the study of the behavior of light in a medium whose optical properties are themselves a function of the light intensity. Pretty much all material exhibit nonlinear optical effects if the light is intense enough, but "intense enough" is frequently in the neighborhood of 10^20 watts per square meter.
Once lasers were invented…
mspringer | November 10, 2010There was some dissension in the comments of my post on solving the Schrodinger equation with a linear potential. What the post boiled down to was that the solution was Ai(u), where we found that u was:
The point of the post was to work through and get that coefficient that's in front of the (Fx + E). The point wasn't to actually solve a physics problem with that, so I glossed over the fact that in solving the physical problem we'll need to deal with boundary conditions, which means paying attention to both types of Airy function Ai(u) and Bi(u), as well as taking into account that only…
mspringer | November 7, 2010Most textbooks, especially ones not aimed at college math majors, give a definition of "function" that seems quite intuitive. They'll say something along the lines of: a function is a rule that takes an input x and turns it into an output f(x). Formally this isn't quite right - the essence of a function is in the set of ordered pairs {x, f(x)} and not in the specific rule that connects them. There doesn't even have to be such a rule.
But the idea of function as a machine is such a powerful and intuitive one that it tends to be used pretty universally until you have a good reason to abandon it…
mspringer | November 5, 2010So consider the one-dimensional time-independent Schrodinger equation:
In some ways it's not really an equation as such, because you have to plug in some function V(x) that describes the potential in the problem you're solving. When you first learn quantum mechanics you'll learn the big ones: V(x) = 0, V(x) = V > E, V(x) = 1/2 kx^2, V(x) = k/x, etc. One that's conspicuously absent is usually one of the simplest looking potentials: V(x) = -Fx. That's just the potential of a constant force, say a particle in a uniform gravitational field. Rarely do textbook authors bother to work out a…