The human eye is sensitive to a portion of the electromagnetic spectrum that we call visible light, which extends from around 400 to 700 nanometer wavelength, peaking in the general vicinity of greenish light at 560 nanometers:
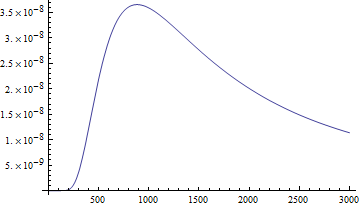
Here's the intensity (formally: power per area per unit solid angle per unit wavelength - whew!) of the radiation emitted by an object with the temperature of the sun, plotted as a function of wavelength in nanometers according to Planck's law:
$latex B_\lambda(T) =\frac{2 hc^2}{\lambda^5}\frac{1}{ e^{\frac{hc}{\lambda k_\mathrm{B}T}} - 1}&s=1$
Spectral radiance (W/(sr m^3)) vs. wavelength (nm)
You'll notice it also peaks around the same place as the spectral response of the human eye. Optimization!
Or is it? That previous equation was how much light the sun dumps out per nanometer of bandwidth at a given wavelength. But nothing stops us from plotting Planck's law in terms of the frequency of the light:
$latex B_\nu(T) = \frac{ 2 h \nu^3}{c^2} \frac{1}{e^\frac{h\nu}{k_\mathrm{B}T} - 1}&s=1$
Spectral radiance (W/(sr m^2 Hz)) vs. frequency (Hz)
In this case what's on the y axis is power per area per unit solid angle per frequency. Ok, great. But notice it's not just the previous graph with f given by c/λ. It's a different graph, with different units. To see the difference, let's see this radiance per frequency graph with the x-axis labeled in terms of wavelength:
Spectral radiance (W/(sr m^2 Hz)) vs. wavelength (nm)
Well. This is manifestly not the same graph as the radiance per nanometer. Its peak is lower, in the near infrared and outside the sensitivity curve of the human eye. This makes some sense - there's not much frequency difference between light with wavelength of 1 kilometer and light with wavelength of 1 kilometer + 1 nanometer. But light of 100 nanometer wavelength has a frequency about 3 x 1013 Hz more than light with wavelength 101 nanometers.
So what gives? Is the eye most sensitive where the sun emits the most light or not? The simple fact of the matter is there's no such thing as an equation that just gives "how much light the sun puts out at a given wavelength". That's simply not a well-defined quantity. What is well defined is how much light the sun puts out per nanometer or per hertz. In this sense our eye isn't optimized so that its response peak matches the sun's emission peak, because "the sun's peak" isn't really a coherent concept. The sensitivity of our eyes is probably more strongly determined by the available chemistry - long-wavelength infrared light doesn't have the energy to excite most molecular energy levels, and short-wavelength ultraviolet light is energetic enough to risk destroying the photosensitive molecules completely.
This wavelength/frequency distribution function issue isn't just a trivial point - it's one of those things that actually gets physicists in trouble when they forget that one isn't the same thing as the other. For a detailed discussion, I can't think of a better one than this AJP article by Soffer and Lynch. Enjoy, and be careful out there with your units!
- Log in to post comments
More like this
I have a favourite graph from a physics textbook. It's really wonderful. Jackson's Classical Electrodynamics, the second edition. Page 291, Figure 7.9. The absorption coefficient for liquid water as a function of linear frequency. It's quite striking. EM radiation at 1e+14 Hz has an absorption coefficient of 1e4 inverse cm. Then, over less than two decades of frequency, the absorption plummets almost 8 decades to the middle of the visible spectrum. Then, over the next decade in frequency again, the absorption climbs by 10 decades. Because our eyes contain a large amount of liquid water, simple intraocular absorption limits us to a frequency range between about 2e+14 and 1.1e+15 Hz. If the absorption coefficient is more than about 3 or 4 inverse cm, there will be high attenuation between the lens and the retina.
Some insect eyes don't have the large amount of free water inside them, and have a shorter distance from outside the eye to the imaging surface, and so can adapt to a wider frequency range, but when your eye is a bag of mostly water the size of a grape, it'll have a frequency response not terribly far from that of humans.
It's also worth noting that when you're talking about "most of the light" you're really talking about is "most of the light energy." You can also make a case, even though our senses are tuned to quantity of energy, that "amount of light" is better thought of as "amount of photons." Then you get two more peaks to play with. :)
Another plausible curve is energy vs the logarithm of wavelength (or frequency, other than a sign flip it won't make any difference), which peaks at around 610 nm. You can also the wavelength where 50% of the energy is above it (about 710) or the wavelength where 50% of the photons are shorter (don't have that on hand).
However, it's certainly not most of the light, since 400-700 nm is only about 37% of the light.
Matt Springer: "So what gives? Is the eye most sensitive where the sun emits the most light or not?"
It isn't at all clear why it would be necessary to have the sensitivity peak at the same place.
Put another way, it might be more useful to have the sensitivity peak somewhere other than where the sun emits the most light.
A couple of colleagues of mine recently wrote a paper on exactly this subject, arguing for a different pedagogical presentation of blackbody radiation. I haven't read it all that carefully, but it seems worth plugging here.
I like it. It makes much more sense than most presentations.
My only reservation is my own Willis Lamb style prejudices about "number of photons emitted per second", because "number of photons" is not well-defined for classical thermal radiation.
Similar to what chad's colleagues suggest wouldn't it be more appropriate, in the case of eye development, to compare the photon flux of relevant light sources (in this case the sun) with the energy dependent quantum efficiency of the eye? Anyone knows how that would look?
I should check it myself, but the one-year-old pulling in my arm thinks otherwise, so I'm just throwing out the suggestion.
I believe I missed something in your reparameterization of B(T). Why does one version have lambda^-5 while the other has nu^3? This does not work if lambda*nu = c.
Nevermind, the wikipedia page shows the differential relation for the reparameterization...