Earlier this week, I showcased the newly-released Hubble Ultra Deep Field in the infrared, and compared it with the older image of the same region taken in visible light.
As many astute readers noticed, the newer image looks blurrier than the old one! This is true, and there's a good reason for this. Here's one of the old images from the Ultra Deep Field (in visible light):

and here's that same region in infrared light.

Yes, the latter image is blurrier. Why is it blurrier? One of the biggest differences between infrared light and visible light is their wavelengths; visible light goes from about 400 to 700 nanometers, but infrared light has a longer wavelength than visible. In fact, as you get redder and redder (or infra-redder, as the case may be), your wavelength continues to increase substantially.
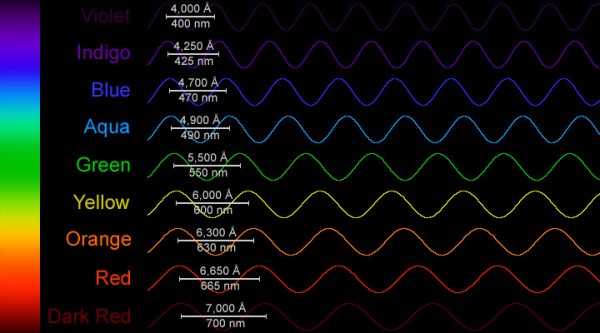
Hubble's new camera, in the infrared, can see from about 800 to 1700 nanometers, or wavelengths more than twice as long as visible light! Well, your telescope's resolution, or how sharply you can see, is directly related to the wavelength of light you look at.
Why is that? Take a look at the Hubble Space Telescope's mirror:

It's got a certain, fixed diameter (2.4 meters). If you send violet light (400 nm) at it, it takes 6 million wavelengths to get across it, meaning it can resolve angles down to 0.034 arc-seconds! (Remember, there are 60 arc-minutes in one degree, and 60 arc-seconds in one arc-minute.) But if you look at the longest wavelength infrared light that Hubble can see (1700 nm), it only takes 1.4 million wavelengths before the light gets across the mirror, meaning that it has a resolution of 0.146 arc-seconds, more than four times worse than the violet light case!
So that's why the newer image looks blurrier, because you're looking at a longer wavelength of light! Incidentally, that's why lone radio telescopes are as big as they are -- even built into mountains, sometimes -- because the wavelength of radio light is measured in meters, not nanometers! Here's a shining example: the 305 meter Arecibo telescope!

So why? Why would we look in a wavelength with inferior resolution? Because resolution isn't the only important factor for astronomy. When galaxies are far away, the light from them gets redshifted, meaning you need to look at longer wavelengths to find them. You look in the infrared instead of the visible, and suddenly you're able to see at higher redshifts, and hence greater distances! Can you spot any blobs in the newer, fuzzier images that simply don't exist in the older one? If you can, you've likely found a new, high-redshift galaxy! Take a look at this side-by-side view of a tiny region of both images:

That extra bright red spot on the left? That's an ultra-high-redshift galaxy that cannot be seen in visible light! Know what else is probably an ultra-high-redshift galaxy? That green smudge below and to the left of the bright red spot; it isn't in the old image!
So you can be upset all you want at the lower resolution; there's plenty of fantastic science that we need the infrared for! And if you just can't see how the infrared will ever compete with the visible, remember that the James Webb Telescope is coming up. It's an infrared space telescope, and it's just a little bigger than Hubble.
Any galaxy hunters out there are free to go to the old HUDF and the new HUDF images and see what you can find. If you find anything good, let us know here!

I just had to take issue with this..
"One of the biggest differences between infrared light and visible light is their wavelengths"
"one of the"?? It's the definition!! Heck, it's the only fundamental difference... Everything else derives from it...
(Of course, you could go by frequency, but it's just the same..)
Regardless, I love your posts! :) Keep informing us
The other difference in the two deep fields are exposure duration; the older deep field is two weeks of exposure, while the new one is "only" two days. This is why the new one appears noisier. This also contributes to the lower resolution; to display the same objects in both images, the new data had to be "stretched" more to match the old data. This leads to more bloating of stars and brighter objects. I suspect many more 8+ redshift objects would be discernable in the field if the new shot had such a long cumulative exposure; increased signal-to-noise ratio.
Sean,
That is also a factor. Resolution is linear in wavelength (i.e., half the wavelength, double the resolution), but goes as the square root of exposure time (i.e., 7 times as long means you can see objects that are â7 times fainter), so I suspect both factors are in play here.
Thanks for the extra info!
@ Oded " . . . it's the only fundamental difference... "
Are you saying photon energy is not fundamental? The photon energy is less for an infra-red photon than one in the visible regime. While energy and wavelength are correlated, they are not the same thing.
Perfect timing. I'm teaching my students about different types of telescopes searching different bandwidths next week!
Good old Arecibo! The only really good reason I can come up with for going back to the Moon is to send construction crews around to the Far Side so they can build the BigAssedest Honkin' Radio Telescope dishes possible in the craters.
Nice piece and nice comments with info.
As a bigger mirro, aren't you forgetting Herschel: http://www.esa.int/SPECIALS/Operations/SEMO4HZTIVE_0.html
@chicagomolly: http://www.lofar.org/ Lofar is going to be ass big as you can go with a 'single' system.
This is very informative, and something I never could have guessed. I think I believe you, too.
It's interesting that the more accurate something is, the blurrier it gets. It could be that space itself is a bit blurry, a la cartes special relativity and quantum mechanics. Interestingly, the same is true in morality.
Cheers and thanks for the lovely photos,
NS
A different, but analogous, effect occurs with increased magnification in any telescope. When you push the lenses to their utmost magnification, you sacrifice clarity, ie. resolution, but gain details you might not see at a lower magnification. If you only need to discern the presence/absence of a very faint or distant object, but not necessarily see it clearly, maximum magnification is preferable, even if it is "fuzzier" than the lower mag.
This is just a quibble, but the wavelengths we use in radio astronomy are better measured in centimeters than meters. By the time they get as long as six or ten meters they start bouncing off the ionosphere - great if you want to talk to people over the horizon, but terrible if you want to look at stars and galaxies. The classic radio frequency band is 20cm; some work is done at 1m, but more and more is being done with wavelengths from 1mm-10cm (in particular the Cosmic Microwave Background work).
In fact the ionosphere is one of the main selling points for putting a telescope on the moon. As far as big dishes (or big arrays) go, it's vastly cheaper to put them on the Earth. But if you want to look at the longest wavelengths, you have to get outside the ionosphere. A telescope on the moon looking at hundred-meter wavelengths would open up a totally new window on the universe.
I found nine ultra-high redshift galaxies. You can see them and the process I went through on my Web site.
Dave,
That is AMAZING! Thanks so much for sharing that!
Amazing? Thank you, but I'm not sure that such a superlative applies. After all, the folks who do this sort of thing for a living probably have vastly superior algorithms (ones which won't lose an IR galaxy within the glow of a visible-light galaxy like mine will) and could actually tell you the distance to all those little blobs.
Of course, they would also start with data that hasn't been JPEG compressed. [wink]
Dr. Plait offers up the wavelengths used for false-coloring the infrared image. I'm wondering if there might be some utility in separating them out, in terms of highlighting which galaxies are more ultra-highly redshifted than others (for example, the nearly monochromatic blob of red that is candidate #178 suggests that it's so far away that it's almost shifted out of the infrared spectrum used for the image, too).
But then again, are the very red galaxies in the visible-light image necessarily redshifted, or are they just full of very old stars? I imagine that a more-detailed spectrum is required to tell the difference, and these two images with their six spectral data points can't tell us that much.
Is the visible-light image even colored true?
Why is the reflection of the workers in the Hubble mirror different? There are 2 people squatting and one standing, while the reflection shows 4 people: one is even pointing at the mirror. This is not reflected in the observers.
Am I nuts here?
Why would someone feel the need to doctor such a simple photo?
I think the people in the reflection are standing out of frame to the right, a little ways back from the mirror; after all, the mirror is curved.
If you look at the white hood on the head of the left-most squatting guy, it seems to jut out to the left along the edge of the mirror. I think that jutting bit of white is actually the reflection of the hood of the person squatting on the right... Follow that line of reflection and you can see the people must be standing back to the right somewhere.